本文主要是介绍【优化】拉格朗日(Lagrange)乘子法超简说明,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文不做数学推导,从物理意义上讲解拉格朗日乘子法。
原问题
我们要解决带有等式约束的最优化问题。为方便书写,以二维函数为例:
m a x f ( x , y ) , s . t . g ( x , y ) = 0 max\ f(x,y), \ \ s.t. g(x,y)=0 max f(x,y), s.t.g(x,y)=0
用下图表示这个问题。 f ( x ) f(x) f(x)参数在二维平面内,其本身是一个曲面,用等高线(蓝色)表示。 g ( x ) = 0 g(x)=0 g(x)=0是二维平面内的一条曲线(红色)。
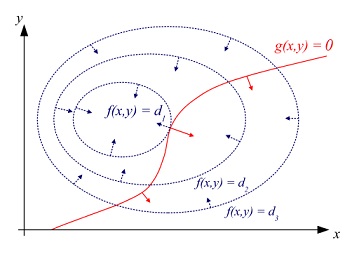
我们要找 g ( x , y ) = 0 g(x,y)=0 g(x,y)=0上的一个点,其位于 f ( x , y ) f(x,y) f(x,y)最大的等高线上。
问题转换
Step 1
求解上述问题等价于:
找到 g ( x , y ) = 0 g(x,y)=0 g(x,y)
这篇关于【优化】拉格朗日(Lagrange)乘子法超简说明的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



