乘子法专题
Lingo学习—— 拉格朗日乘子法 KKT条件
目录 一、初识拉格朗日乘子法和KKT条件 什么是拉格朗日乘子法? 二、最优化问题会碰到一下三种情况: (1)无约束条件 (2)等式约束条件 例题1.1:求椭球内接长方体 的最大体积。 例题1.2:(用LINGO求解)求原点到椭圆的最短距离。 (3)不等式约束条件 参考文章:(如侵权,请联系我删除) 一、
理解拉格朗日乘子法的一种角度
目录 梯度和等高域正交 某点在各个约束条件的梯度是该点的约束域邻域的正交域的一组基,几乎处处成立 极值点的必要条件为约束域邻域和目标梯度正交 本文旨在以一种相对直观的角度去理解拉格朗日乘子法,在推导得到拉格朗日乘子法最终形式之前,需要先理解以下三个推论: 1. 梯度和等高域邻域正交(或者说某点梯度和该点在等高域相切的超平面正交); 2. 极值点在
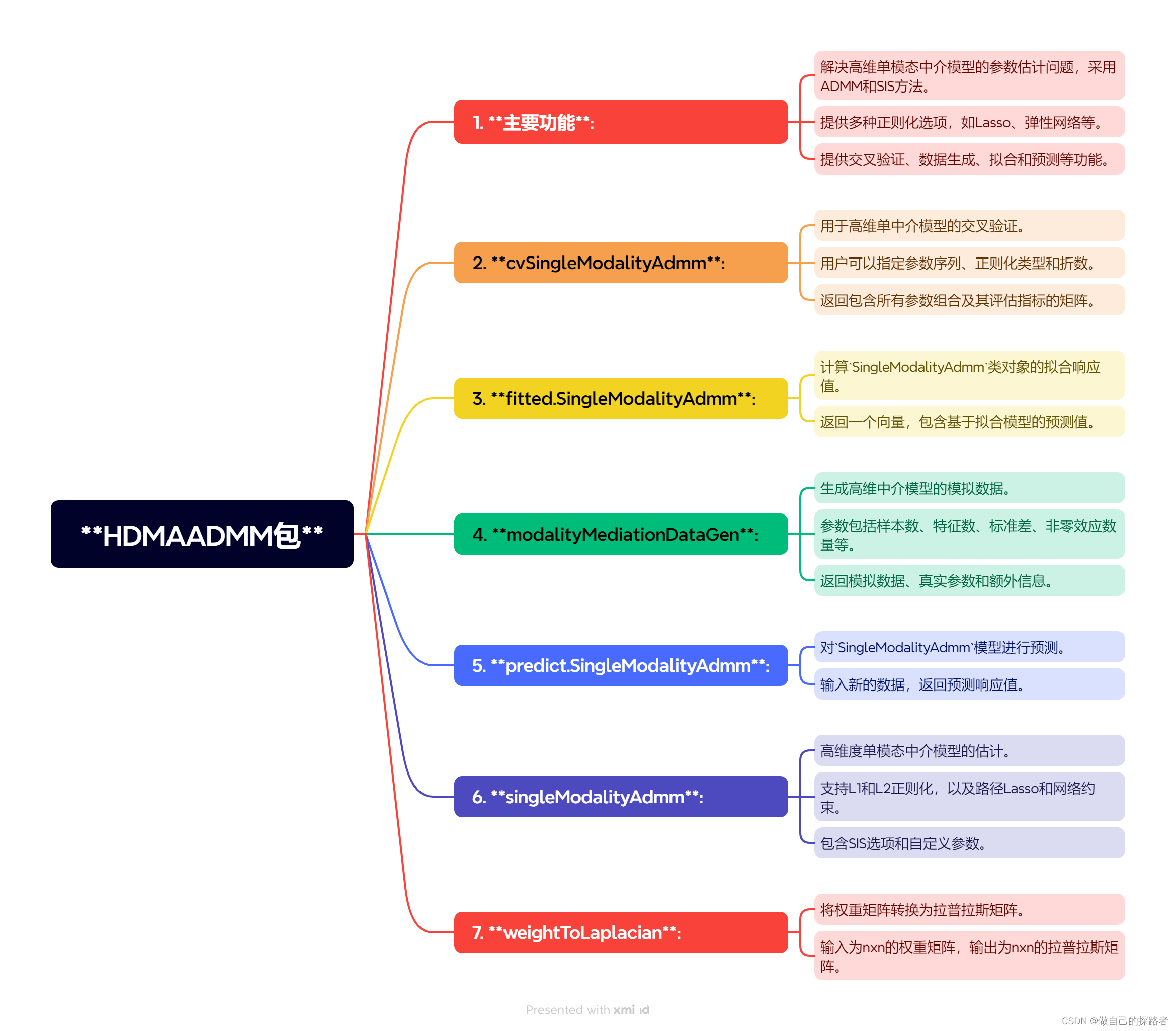
高维中介数据:基于交替方向乘子法(ADMM)的高维度单模态中介模型的参数估计(入门+实操)
全文摘要 用于高维度单模态中介模型的参数估计,采用交替方向乘子法(ADMM)进行计算。该包提供了确切独立筛选(SIS)功能来提高中介效应的敏感性和特异性,并支持Lasso、弹性网络、路径Lasso和网络约束惩罚等不同正则化方法。 Pathway Lasso 背景 传统的结构方程建模(SEM)在处理大量中介变量时变得不稳定且计算复杂。Pathway Lasso引入了一个新的惩罚函数,它是一
svm的对偶,kkt,拉格朗日乘子法
原文链接:https://blog.csdn.net/bit_666/article/details/79865225 1.SVM基础模型 给定训练集D={(x1,y1),(x2,y2)...(xn,yn)},yi∈{-1,1},例如下面图中的点,蓝线左上方的6个点对应1类,右下方的6个点对应-1类,基于数据分类的思想,如果我们想把两类数据分开,显然蓝线不是唯一的选择,我们有无数条直线可以选择
约束极值问题之拉格朗日乘子法、KKT条件与对偶理论
文章目录 1 等式约束极值问题1.1 拉格朗日乘子法(必要条件) 2 不等式约束极值问题2.1 约束作用2.2 不等式约束的几何解释2.3 下降方向2.4 可行方向2.5 Fritz John条件(最优解必要条件)2.6 Kuhn-Tucker条件(最优解必要条件 - 约束规格)2.7 最优解必要条件 3 对偶问题3.1 原始问题的等价问题3.2 原始问题的对偶问题3.3 原始问题与对偶问题
理解拉格朗日乘子法与KKT条件
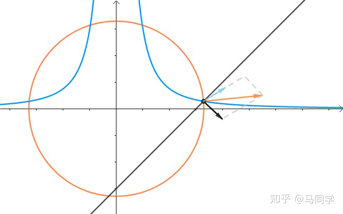
理解拉格朗日乘子法与KKT条件 拉格朗日乘子法 https://www.matongxue.com/madocs/939.html 看完小结: 对于曲线 z1=x2+y2 和曲线 z2=y*(x**2) 。z2=3时,在两曲线的相切点,两曲线的梯度向量平行 拉格朗日法与KKT条件 https://mp.weixin.qq.com/s/SnHGG7ZEZ9SJapPmWhhHpQ 注意图
matlab 最小二乘拟合平面(拉格朗日乘子法)
目录 一、算法原理二、代码实现三、结果展示 本文由CSDN点云侠原创,原文链接。博客长期更新,爬虫自重。 一、算法原理 设拟合出的平面方程为: a x + b y &#
【优化】拉格朗日(Lagrange)乘子法超简说明
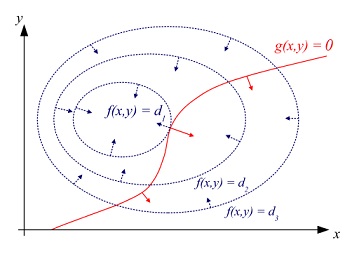
本文不做数学推导,从物理意义上讲解拉格朗日乘子法。 原问题 我们要解决带有等式约束的最优化问题。为方便书写,以二维函数为例: m a x f ( x , y ) , s . t . g ( x , y ) = 0 max\ f(x,y), \ \ s.t. g(x,y)=0 max f(x,y), s.t.g(x,y)=0 用下图表示这个问题。 f ( x ) f(x) f(x
约束优化之Lagrange乘子法KKT条件对偶问题最容易理解解读
1.无约束优化的常用方法 在讲带约束优化方法之前,我们先简单回顾一下常用的无约束优化方法。 1.梯度下降法 2.牛顿法/拟牛顿法 3.共轭梯度法 … 上面梯度系列的无约束条件下的最优化,基本解法是根据极值的必要条件一阶导数为0,通过泰勒展开等形式,构造不同数列不断逼近最优解。 2.带约束的优化 实际情况中,不带约束的场景比较少见,大部分都为带约束的优化问题。看一个大家都用的图: 上图中,
理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
转自(http://blog.csdn.net/xianlingmao/article/details/7919597) 在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法,对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值;如果含有不等式约束,可以应用KKT条件去求取。当然,这两个方法求得的结果只是必要条件,
机器学习之拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法,对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值;如果含有不等式约束,可以应用KKT条件去求取。当然,这两个方法求得的结果只是必要条件,只有当是凸函数的情况下,才能保证是充分必要条件。KKT条件是拉格朗日乘子法的泛化。之前学习的时候,只知道直接应用两个方法,但是却
任意一点X0到超平面S的距离以及拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
转自: http://blog.csdn.net/xinzaichenmo/article/details/70161728 http://blog.csdn.net/xianlingmao/article/details/7919597 在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条
拉格朗日乘子法与KKT条件核心原理(小白都能看懂)
文章目录 问题背景等式约束条件下的最优化不等式约束条件下的最优化问题多条件约束下的最优化问题KKT条件 问题背景 假设有一座山,山上有一条路。我们只能走在这条路上,其他的地方无法到达。在此基础上,我想知道我始终在路上的情况下,可能达到的最高点及其高度。 拉格朗日乘子法和KKT条件解决的正是这么个问题。我们想知道在某个约束条件(山间小路)的限制下,所能达到的最值点(最大高度)。是
深入理解拉格朗日乘子法和KKT条件的原理及运用
深入理解拉格朗日乘子法和KKT条件的原理及运用 一、凸函数二、常见的三类最优化问题三、拉格朗日乘子法解决带等式约束的最优化问题(一)用实例理解拉格朗日乘子法的背后意义(二)、拉格朗日乘子法求解带等式约束的最优化问题 四、引入KKT条件求带不等式约束条件的最优化(一)实例理解带不等式约束条件的最优化(二)满足KKT条件下的利用拉格朗日函数求带不等式约束的最优化问题(三)原最优化问题转对偶问题