本文主要是介绍Lingo学习—— 拉格朗日乘子法 KKT条件,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、初识拉格朗日乘子法和KKT条件
什么是拉格朗日乘子法?
二、最优化问题会碰到一下三种情况:
(1)无约束条件
(2)等式约束条件
例题1.1:求椭球内接长方体 的最大体积。
例题1.2:(用LINGO求解)求原点到椭圆的最短距离。
(3)不等式约束条件
参考文章:(如侵权,请联系我删除)
一、初识拉格朗日乘子法和KKT条件
什么是拉格朗日乘子法?
在数学最优问题中,拉格朗日乘子法(Lagrange Multiplier)
:是一种寻找变量 受一个或多个条件限制的 多元函数的 极值的方法。
这种方法将一个有 n 个变量与 k 个约束条件的最优化问题 转换为一个有 n + k 个变量的方程组的极值问题,其变量不受任何约束。
(可以理解为:约束和变量同时都成为了变量)
这种方法引入了一种新的标量未知数,即 拉格朗日乘数 :
约束方程的梯度(gradient)的线性组合里每个向量的系数。
什么时候需要 拉格朗日乘子法?
答:多变量、多等式约束条件 求极值
在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法。
在 有等式约束 时使用拉格朗日乘子法,
在 有不等约束 时使用KKT条件。
我们这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值
(因为最小值与最大值可以很容易转化,即最大值问题可以转化成最小值问题)。
KKT条件 与 拉格朗日乘子法 二者均是求解最优化问题的方法,不同之处在于应用的情形不同。
二、最优化问题会碰到一下三种情况:
(1)无约束条件
这是最简单的情况,解决方法通常是函数对变量求导,令求导函数等于0的点可能是极值点。将结果带回原函数进行验证即可。
(2)等式约束条件
设目标函数为f(x),约束条件为h_k(x),我们称:
为等式约束条件。
则解决方法是消元法或者拉格朗日法。
例题1.1:
给定椭球: 求这个椭球的 内接长方体 的最大体积。
解答:
这个问题实际上就是 条件极值问题,即在条件 下,
求 的最大值。
当然这个问题实际可以先根据条件消去 z (消元法),然后带入转化为无条件极值问题来处理。
但是有时候这样做很困难,此时我们用拉格朗日乘数法。
首先 定义拉格朗日函数 F(x):
( 其中λ、k是各个约束条件的待定系数)
然后解变量的偏导方程:
......
如果有m个约束条件,就应该有m+1个方程。
求出的方程组的解就可能是 最优解(高等数学中提到的极值)
将结果带回原方程验证就可得到解。
回到上面的题目,通过拉格朗日乘数法将问题转化为:
对 求偏导得:

联立前面三个方程得到

和 
带入 第④个 方程 解得:

带入解得最大体积为:

PS:深层理解做法:为什么这么做可以求解最优解?(不深究原理的可自行跳过)
举个二维 最优解的例子:
min f(x,y)
s.t. g(x,y) = c
这里画出 z = f(x,y) 的等高线 :

绿线标出的是约束 g(x,y)=c 的点的轨迹。
蓝线是f(x,y)的等高线。
箭头表示斜率,和等高线的法线平行。
从梯度的方向上来看,显然有d1>d2。绿色的线是约束,也就是说,只要正好落在这条绿线上的点才可能是满足要求的点。如果没有这条约束,f(x,y)的最小值应该会落在最小那圈等高线内部的某一点上。
而现在加上了约束,最小值点应该在哪里呢?
显然应该是在f(x,y)的等高线正好和约束线相切的位置,因为如果只是相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部,使得新的等高线与目标函数的交点的值更大或者更小,只有到等高线与目标函数的曲线相切的时候,可能取得最优解。
如果我们对约束也求梯度 ∇g(x,y) ,则其梯度如图中绿色箭头所示。
很容易看出来,要想让目标函数f(x,y)的等高线和约束相切,则他们切点的梯度一定在一条直线上 ( f 和 g 的斜率平行)。
也即在最优解的时候:
其中∇为梯度算子;
即:f(x)的梯度 = λ*g(x) 的梯度,λ是常数,可以是任何非0实数,表示左右两边同向。
即:
那么拉格朗日函数:
在达到极值时 F(x,y) 与 f(x,y) 相等,因为 F(x,y) 达到极值时 g(x,y)−c 总等于零。
min( F(x,λ) ) 取得极小值时 其导数为0,即:
也就是说 f(x) 和 h(x) 的梯度共线。
简单的说,在F(x,λ)取得最优解的时候,
即 F(x,λ) 取极值(导数为0,)的时候,
f(x)与g(x) 梯度共线,此时就是在条件约束g(x)下,f(x)的最优解。
例题1.2:(用LINGO求解)
抛物面 被平面
截成一椭圆,
求原点到这椭圆的最短距离。
解答:
该问题可以用拉格朗日乘子法求解。下面把问题归结成数学规划模型,用LINGO求解。
设原点到椭圆上点(x,y,z) 的距离最短,建立如下数学规划模型: (s.t. => subject to 即“受限于”)

LINGO求解程序如下:
min = (x^2+y^2+z^2)*(1/2);
x+y+z = 1;
z = x^2 + y^2;
@free(x);
@free(y);PS:LINGO中默认所有变量都是非负的,这里的 x, y 的取值可正可负,所以使用@free函数
@free(x):取消对变量x 的默认下界为 0 的限制,即 x 可以取任意实数。
运行结果如下:
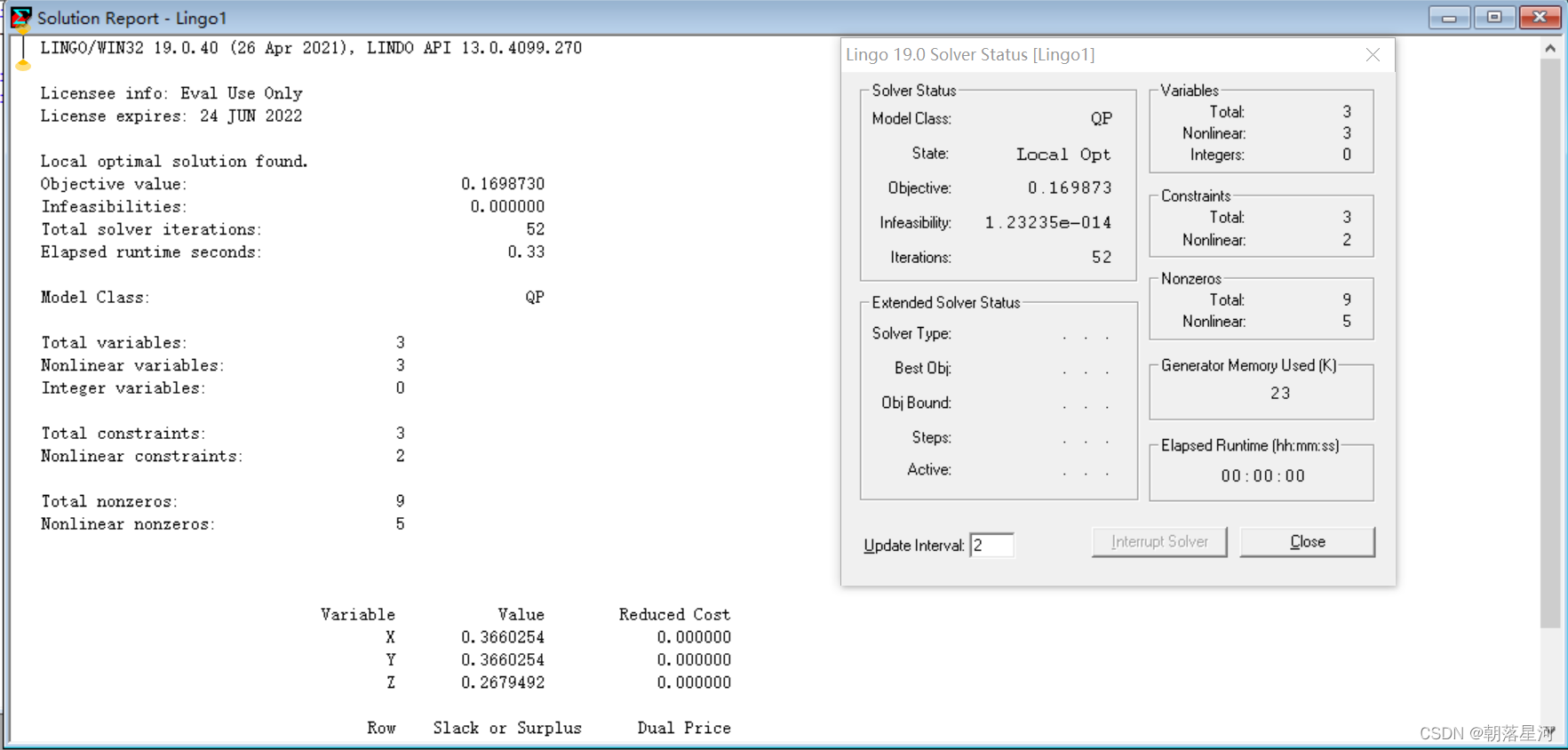
(3)不等式约束条件
设目标函数f(x),不等式约束为g(x),有的教程还会添加上等式约束条件h(x)。
此时的约束优化问题描述如下:
则我们定义不等式约束下的拉格朗日函数 L,则 L表达式为:
其中 f(x) 是原目标函数, 是第 j 个等式约束条件,
是对应的约束系数,
是不等式约束,
是对应的约束系数。
常用的方法是KKT条件,同样地,把所有的不等式约束、等式约束和目标函数全部写为一个式子:
,
KKT条件的最优值必须满足以下条件:
1)L(a, b, x) 对 x 求导为零;
2)h(x) =0;
3)a*g(x) = 0;
求取这些等式之后就能得到候选最优值。其中第三个式子非常有趣,因为 ,如果要满足这个等式,必须a=0或者g(x)=0。
这是SVM的很多重要性质的来源,如支持向量的概念。
接下来主要介绍KKT条件,推导及应用。详细推导过程如下:


参考文章:(如侵权,请联系我删除)
1. 拉格朗日乘数法_ACdreamer-CSDN博客_拉格朗日乘数法
2. 拉格朗日乘子法(Lagrange Multiplier) - 知乎 (zhihu.com)
3.一文看懂支持向量机 SVM(附:6个有点+5个缺点) (easyai.tech)
4. KKT条件介绍_johnnyconstantine的专栏-CSDN博客_kkt条件
5.【整理】深入理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件 - mo_wang - 博客园 (cnblogs.com)
这篇关于Lingo学习—— 拉格朗日乘子法 KKT条件的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





