拉格朗专题
最优化方法Python计算:二次规划的拉格朗日算法
目标函数为二次式,约束条件为线性式的最优化问题称为二次规划。其一般形式为 { minimize 1 2 x ⊤ H x + c ⊤ x s.t. A e q x − b e q = o A i q x − b i q ≥ o . \begin{cases} \text{minimize}\quad \frac{1}{2}\boldsymbol{x}^\top\boldsymbol{Hx}+\
先从路径优化开始学习FastPlanner之B样条曲线平滑路径(一):从拉格朗日插值到B样条曲线
参考B站视频学习 注:我会列出学习他人的博客,但我不涉及具体推导,原理讲解,旨在于理解必须概念后写代码出效果。 给若干点如何获得一条平滑的曲线? 两个方法插值、拟合 插值要经过给定点,拟合不用经过。 经典插值方法:拉格朗日插值法和牛顿插值法。 区别: 拉格朗日插值法 优点 简单易懂: 拉格朗日插值法公式简单直观,易于理解和实现。无需求导: 拉格朗日插值法不需要对函数进行求导,只需知
SVM(二)从拉格朗日对偶问题到SVM
2.1 拉格朗日对偶(Lagrange duality) 先抛开上面的二次规划问题,先来看看存在等式约束的极值问题求法,比如下面的最优化问题: 目标函数是f(w),下面是等式约束。通常解法是引入拉格朗日算子,这里使用来表示算子,得到拉格朗日公式为 L是等式约束的个数。 然后分别对w和求偏导,使得偏导数等
Python | C# | MATLAB 库卡机器人微分运动学 | 欧拉-拉格朗日动力学 | 混合动力控制
🎯要点 🎯正向运动学几何矩阵,Python虚拟机器人模拟动画二连杆平面机械臂 | 🎯 逆向运动学几何矩阵,Python虚拟机器人模拟动画三连杆平面机械臂 | 🎯微分运动学数学形态,Python模拟近似结果 | 🎯欧拉-拉格朗日动力学数学形态,Python模拟机器人操纵器推导的运动方程有效性 | 🎯运动规划算法,Python虚拟机器人和摄像头模拟离线运动规划算法 | 🎯移动导航卡尔曼
拉格朗日(Lagrange)插值曲线
简介 拉格朗日(Lagrange)插值曲线是最简单的一种插值曲线。假设给定控制点(Xi, Yi)(i = 0,1,…,n),拉格朗日差值方法构造出一个不超过n次的插值多项式Pn(x)。得到的差值公式为: 代码 此段代码用于从一致的一系列控制点生成一系列点构成的插值曲线。 //xmax 为控制点中最大的横坐标//xmin 为控制点中最小的横坐标/
自然数幂和 拉格朗日插值法和第二类斯特林数法
写在这里,目的是在以后需要看的时候不用再去网上抄(划掉) 求 s ( n ) = ∑ i = 1 n i k 求s(n)=\sum_{i=1}^n i^k 求s(n)=i=1∑nik 拉格朗日插值法 给定若干个点值,(x0,y0),(x1,y1),(xn,yn),它们的差值多项式 L ( x ) = ∑ i = 0 n y i ∗ ∏ j ≠ i x − x j x i − x j L(
拉格朗日插值法 C语言实现
/* *作者:KDF5000 *功能:利用拉格朗日插值法求解近似值 *时间:2013.4.15 */ #include <stdio.h> #include <stdlib.h> #include <string.h> //存放插值节点 struct Data{ double x; double y; struct Data *
SVM中的拉格朗日乘数法和KKT条件的深入解析
在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法,对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值;如果含有不等式约束,可以应用KKT条件去求取。当然,这两个方法求得的结果只是必要条件,只有当是凸函数的情况下,才能保证是充分必要条件。KKT条件是拉格朗日乘子法的泛化。之前学习的时候,只知道直接应用两个方法,但是
Lingo学习—— 拉格朗日乘子法 KKT条件
目录 一、初识拉格朗日乘子法和KKT条件 什么是拉格朗日乘子法? 二、最优化问题会碰到一下三种情况: (1)无约束条件 (2)等式约束条件 例题1.1:求椭球内接长方体 的最大体积。 例题1.2:(用LINGO求解)求原点到椭圆的最短距离。 (3)不等式约束条件 参考文章:(如侵权,请联系我删除) 一、
解决拉格朗日四平方和定理
1 问题 “拉格朗日四平方数和定理”是数学中著名的一个定理,其内容为:任意一个正整数均可表示为四个整数的平方和(其中有些整数可以为零)。要求输入一个数,找出所有符合该定理的四个整数? 2 方法 可以通过“四平方数和定理”的含义来解决,即四个整数的平方和,最后等于用户输入的数值。这里采用最简单的循环来解决,分别给出四个循环,判断这四个循环,循环出来的数的平方和是否等于用户输入的值,如果等于用户输入
[机器学习必知必会]拉格朗日法及其对偶问题
了解一些简单的数学概念 首先看一个二元函数(再复杂一点的函数就很难直观地呈现出来)的三维图像和对应的等高线,其中函数表达式为 z = x 2 + y 2 z=x^2+y^2 z=x2+y2: 从导数到偏导数 对于一个一元函数而言,导数的定义想必大家都很清楚,具体的表达式为: f ′ ( x ) = lim △ x → 0 f ( x + △ x ) − f ( x ) △ x =
基于拉格朗日分布算法的电动汽车充放电调度MATLAB程序
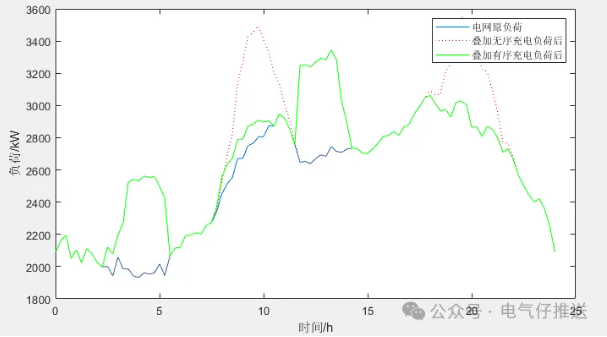
微❤关注“电气仔推送”获得资料(专享优惠) 程序简介 该模型主要做的是基于拉格朗日分布算法的电动汽车充放电调度模型。利用蒙特卡洛模拟法模拟出电动汽车负荷曲线,并求解出无序充电功率曲线和有序充电曲线,该模型在电动汽车个体充放电模型中,采用拉格朗日分布算法,考虑电动汽车不同充电情况表现,同时考虑了电动汽车每天可能会多次接入充电桩的情况。程序采用matlab编写,注释清晰,方便学习。 部分代码
LOJ#2473. 「九省联考 2018」秘密袭击(线段树合并+拉格朗日插值)
一个非常强的题。 也许比较套路但是都比较生疏。 主要使用两个思想。 首先是把求第k大的权转化成枚举i 从1 - W 计算 最终的第k大 大于等于 i 的和。 然后就可以 转化成一个DP。 f[i][j][k] represents the subtree of the node i and we are considering the value of the kth node is not le
智乃酱的静态数组维护问题多项式(拉格朗日插值求高阶差分)
题目链接 智乃酱的静态数组维护问题多项式 题目大意 有 n n n 个数 a [ 1 ] , a [ 2 ] , ⋯ , a [ n ] a[1], a[2], \cdots, a[n] a[1],a[2],⋯,a[n]. m m m 次操作,每次操作给出一个多项式函数 f ( x ) = ∑ i = 0 k c i x i f(x) = \begin{aligned} \sum_
拉格朗日插值法——matlab代码实现
公式: function y=lagrange(x0,y0,x)% 给定一系列点x0,y0 % x是我们要预测的值,由于可以有多个,因此用向量表示% y返回我们的估计值,由于可以有多个,因此用向量表示n = length(x);% 要预测的个数y = zeros(n);% 初始化,并赋初值0for k = 1:length(x0)j_no_k=find((1:length(x0))~=k
理解拉格朗日乘子法的一种角度
目录 梯度和等高域正交 某点在各个约束条件的梯度是该点的约束域邻域的正交域的一组基,几乎处处成立 极值点的必要条件为约束域邻域和目标梯度正交 本文旨在以一种相对直观的角度去理解拉格朗日乘子法,在推导得到拉格朗日乘子法最终形式之前,需要先理解以下三个推论: 1. 梯度和等高域邻域正交(或者说某点梯度和该点在等高域相切的超平面正交); 2. 极值点在
leetcode279 拉格朗日四平方和定理
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。输入: n = 12 输出: 3 解释: 12 = 4 + 4 + 4. 拉格朗日四平方和定理: 1、对于任意一个正整数都可以表示成至多四个整数的平方和(把0考虑进去了也) 下面剪枝性的来找对任意正整数n可以表示成多少几个整数的平方和 2、 若k%4=0
拉格朗日乘数法什么时候考虑端点?解得的点是什么?
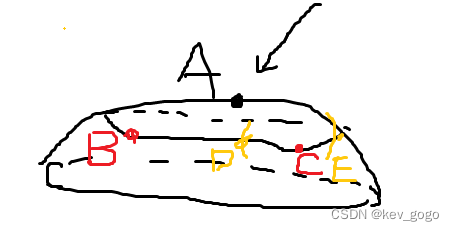
问题提出 2013年的真题有一道题是用拉格朗日乘数法只能求出来一个点,当时很费解,因此查阅相关资料后,对这部分的知识做一个小总结。 无条件极值和条件极值 首先,在求无条件极值的时候,我们求的是曲面上的极值点。 例如: 这个A点就是无条件极值点。 而条件极值则是在原来曲面的基础上,由约束条件截得的曲线上的极值点。 例如: 这里B点和C点就是条件极值点。 求最值 情况1:求边界上的最值
基于拉格朗日乘法优化的Linear SVM 数学推导
对于一个线性可分的二分类数据集,Linear SVM是如何进行work的,这里基于MIT公开课进行了详细的数学推导,后续使用kernal trick的方法的数学推导后续再补上,这里使用拉格朗日乘法优化超平面,当然也可以使用梯度下降的方法,写一篇博客会写一个小程序使用梯度下降的方法,以使自己对SVM梯度下降有个清楚的认识,以便自己以后查阅复试使用。 李航老师对于SVM的章节的综述非常的到位,这里引用
从L1,L2正则,到KKT条件下的拉格朗日乘法到拉格朗日对偶问题
转:相对清晰的一篇博客 从loss的l1,l2正则,追溯到模型复杂度衡量,追溯到不等式极值问题,以下两篇文章,可以进一步深入了解背后的数学原理 L1、L2正则化和过拟合 [从KKT条件下的拉格朗日乘法到拉格朗日对偶问题]
优化|复杂度分析——用于凸约束非凸优化问题的光滑化近似点增广拉格朗日算法
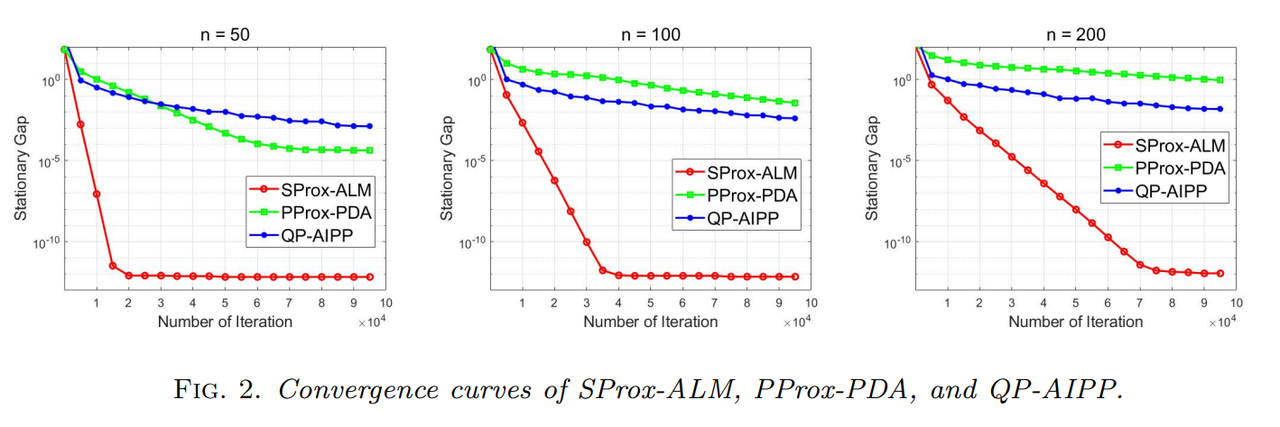
1. 简介 对于无约束的非凸优化问题,算法复杂度的下界为 Ω ( 1 / ϵ 2 ) \Omega(1/\epsilon^2) Ω(1/ϵ2);在目标函数光滑时,这个下界可以通过标准梯度下降算法来取到. 对于带约束的非凸优化问题,这个下界依旧适用;到这里,我们自然会提出疑问:它是否也能通过某个一阶算法来取到? 对此,本文 [ 1 ] ^{[1]} [1]作出了回答. 文中介绍了一种简单的一
【省选模拟】Fac (生成函数)(组合意义)(拉格朗日反演)(倍增)(多项式全家桶)
传送门 没有题解是真的秀,连蒙带猜搞了一天结果今天早上才写完,不过还好有 3 个神仙学长助力 不知道题解是怎么想到的,所以只好直接说结论了 经观察发现可以先求出 ( i k i − 1 ) 1 i \binom{ik}{i-1}\frac{1}{i} (i−1ik)i1,这个在 k = 2 k=2 k=2 的时候是卡特兰数也就是二叉树的个数 考虑将其扩展为 k k k 叉树,即证