优化｜复杂度分析——用于凸约束非凸优化问题的光滑化近似点增广拉格朗日算法

本文主要是介绍优化｜复杂度分析——用于凸约束非凸优化问题的光滑化近似点增广拉格朗日算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 简介

对于无约束的非凸优化问题，算法复杂度的下界为$\Omega (1/{ϵ}^2)$；在目标函数光滑时，这个下界可以通过标准梯度下降算法来取到. 对于带约束的非凸优化问题，这个下界依旧适用；到这里，我们自然会提出疑问：它是否也能通过某个一阶算法来取到？

对此，本文${}^{[1]}$作出了回答. 文中介绍了一种简单的一阶算法——光滑化近似点增广拉格朗日方法（Smoothed Proximal Augmented Lagrangian Method），并证明它可以取到这样的复杂度下界.

2. 问题与算法

2.1 问题背景

考虑
$$\begin{array}{rl}& \min f(x)\\ \text{s.t. }& Ax=b,x\in \mathcal{X},\end{array}(1)$$

其中 $A\in {\mathbb{R}}^{m\times n},b\in {\mathbb{R}}^m$, X = { x ∣ h i ( x ) ≤ 0 , i = m + 1 , ⋯ m + l } \mathcal{X} = \{x ~| ~h_i(x)\leq 0, ~i = m+1,\cdots m+l\} X={x ∣ hi​(x)≤0, i=m+1,⋯m+l} 是凸集，$h_i(\cdot ):{\mathbb{R}}^n\to \mathbb{R}$ 是光滑的凸函数. 目标函数 $f(\cdot ):{\mathbb{R}}^n\to \mathbb{R}$ 未必是凸的，其梯度满足 Lipschitz 连续条件. 不妨将 $\mathcal{X}$ 的指示函数记作 $\iota (\cdot )$，即
$$\iota (x)=\{\begin{array}{ll}0,& \text{当}x\in \mathcal{X},\\ \infty ,& \text{其他}.\end{array}$$
在实际应用中，我们的目标通常是找到问题 (1) 的一个 $ϵ$-稳定点，它的定义为：

定义一 ($ϵ$-稳定点) 我们称 $x\in \mathcal{X}$ 是问题 (1) 的一个$ϵ$-稳定点（$ϵ\ge 0$），当且仅当存在 $y\in {\mathbb{R}}^n$ 和 $v\in \nabla f(x)+A^{T}y+\partial \iota (x)$，满足 $\Vert v\Vert \le ϵ$ 和 $\Vert Ax-b\Vert \le ϵ$.

不难看出，取 $ϵ=0$ 即对应问题 (1) 的稳定点.

2.2 算法框架

对于上述问题，常用的算法有增广拉格朗日算法（ALM）、交替乘子法（ADMM）以及罚函数方法等. 本文所考虑的是一种光滑化的近似点增广拉格朗日算法. 定义投影算子 ${\mathcal{P}}_{\mathcal{X}}(\bar{x})=\arg {\min }_{x\in \mathcal{X}}\Vert x-\bar{x}{\Vert }^2$, 以及函数
$$K(x,z;y)=f(x)+y^T(Ax-b)+\frac{\gamma }{2}\Vert Ax-b{\Vert }^2+\frac{p}{2}\Vert x-z{\Vert }^2,$$

其中常数 $\gamma \ge 0,p>0$.（当 $p=0$ 时，$K(\cdot )$ 即对应问题 (1) 的增广拉格朗日函数.） 算法框架可以写成如下形式：

定义
$$d(y,z)=\underset{x\in \mathcal{X}}{\min }K(x,z;y),x(y,z)=\arg \underset{x\in \mathcal{X}}{\min }K(x,z;y),$$
$$P(z)=\underset{x\in \mathcal{X},Ax=b}{\min }f(x)+\frac{p}{2}\Vert x-z{\Vert }^2,x(z)=\underset{x\in \mathcal{X},Ax=b}{\mathrm{argmin}}f(x)+\frac{p}{2}\Vert x-z{\Vert }^2.$$
可以证明，问题 (1) 等价于
$$\underset{z}{\min }P(z),\text{s.t.}z\in {\mathbb{R}}^n.(2)$$

对于问题 (2) 的最优解 $z^{\ast }$ 而言，$x(z^{\ast })$ 是问题 (1) 的稳定点. 考虑求解问题 (2). 一方面，根据 Danskin 定理可知
$$\nabla P(z)=p(z-x(z)).$$

由于涉及 $x(z)$ 的求解， $\nabla P(z)$ 的精确值往往需要较大的计算量. 另一方面，我们可将算法中对 $y^{t+1}$ 和 $x^{t+1}$ 的更新看作是为求解 $x(z^t)$ 而对原始、对偶变量进行的一步更新，因此 $x^{t+1}$ 相当于 $x(z^t)$ 的一个近似. 这样一来，算法中对于 $z^{t+1}$ 的更新可看作是为求解问题 (2) 而做的一步近似梯度下降.

3. 收敛性结论

3.1 假设条件

结合 2.1 节的描述，文章做出如下假设：

假设1

(1) $\mathcal{X}$ 是一个紧凸集；
(2) $f$ 在 $\mathcal{X}$ 上是下有界的函数（存在 $\underline{f}$，对任意 $x\in \mathcal{X}$ 满足 $f(x)>\underline{f}>-\infty$）；
(3) $f$ 的梯度在 $\mathcal{X}$ 上 $L$-连续，对应 Lipschitz 常数为 $L_f$；
(4) $h_i(i=m+1,\cdots ,m+l)$ 是光滑凸函数，其梯度 $L$-连续，对应 Lipschitz 常数为 $L_h$;
(5) Slater 条件成立.

其中，我们通过 Slater 条件可知 $x^{\ast }\in {\mathbb{R}}^n$ 是问题 (1) 的稳定点当且仅当它满足对应的 KKT 条件.

为了对算法在凸集 $\mathcal{X}$ 上的收敛性进行分析，本文又提出了一个正则性假设. 我们用 $J(x)\in {\mathbb{R}}^{n\times l}$ 表示 $\left(h_1(x),\cdots ,h_l(x)\right)$ 对应的 Jaccobian 矩阵，记 [ m ] = { 1 , ⋯ , m } [m]=\{1,\cdots,m\} [m]={1,⋯,m} 以及 [ m : n ] = { m , m + 1 , ⋯ , n } [m:n] = \{m,m+1,\cdots,n\} [m:n]={m,m+1,⋯,n}. 在此基础上，定义 $Q(x)=[A^T{J}^T(x){]}^T$，积极不等式约束对应的指标集 I x = { i ∈ [ m + 1 : m + l ] ∣ h i ( x ) = 0 } \mathcal{I}_x = \{i \in [m+1:m+l] ~| ~h_i(x)=0\} Ix​={i∈[m+1:m+l] ∣ hi​(x)=0} 以及所有积极约束对应的指标集 ${\mathcal{S}}_x=[m]\cup {\mathcal{I}}_x$. 另外，对于 $\mathcal{S}\subseteq [m+l]$，我们用 $Q_{\mathcal{S}}(x)$ 表示 $Q(x)$ 取出 $\mathcal{S}$ 对应列所得到的矩阵. 利用这些符号，正则性假设可以写成：

假设2 对任意的最优解 $x\in {\mathcal{X}}^{\ast }$, 都存在一个邻域，使得邻域内任意点 $x$ 对应的矩阵 $Q_{{\mathcal{S}}_x}(x)$ 有相同的秩.

在这些条件下，可证明算法对于问题 (1) 有着 $O(1/{ϵ}^2)$ 的收敛速率. 实际上，如果 $h_i(i=m+1,\cdots ,m+l)$ 都是线性的，那么 $\mathcal{X}$ 的紧性、Slater 条件和正则性假设都可以省去，我们只需要假设 2.1 中的条件 (2) 和 (3) 就可以证明上述收敛性结论${}^{[2]}$.

3.2 收敛率证明

结合 3.1 节的内容，本文将势能函数定义为：
$${\varphi }^t=K(x^t,z^t;y^t)-2d(y^t,z^t)+2P(z^t).$$

关于势能函数，可以证明：

引理1 令参数 $p,\gamma ,c,\alpha$ 满足条件 $p\ge 3L_f,\gamma \ge 0,c<1/(L_f+\gamma {\sigma }_{\max }^2(A)+p),\alpha <\frac{c(p-L_f{)}^2}{4{\sigma }_{\max }^2(A)}$.此时存在 ${\beta }^{\prime }>0$，使得对任意的 $\beta \le {\beta }^{\prime }$ 都有
$${\varphi }^t-{\varphi }^{t+1}\ge \frac{1}{8c}{\Vert x^t-x^{t+1}\Vert }^2+\frac{\alpha }{2}{\Vert Ax\left(y^{t+1},z^t\right)-b\Vert }^2+\frac{p}{6\beta }{\Vert z^t-z^{t+1}\Vert }^2.(3)$$

引理的证明过程主要分为三个部分：

(1) 在一定的参数条件下，分别估计 $K(x^t,z^t;y^t)-K(x^{t+1},z^{t+1};y^{t+1})$，$d(y^{t+1},z^{t+1})-d(y^t,z^t)$和 $P(z^t)-P(z^{t+1})$ 的下界表达式，从而得到 ${\varphi }^t-{\varphi }^{t+1}$ 的下界；

(2) 通过原始误差界（Primal Error Bound）的相关结论，结合平方差公式、柯西-施瓦茨公式等简单的运算，将 ${\varphi }^t-{\varphi }^{t+1}$ 的下界进行放缩，得到一个新的下界，它可以被写作几个(带有系数的)范数平方项的代数和（不妨记作 $A+B+C-D$）；

(3) 根据对偶误差界（Dual Error Bound）的相关理论，我们可以提出一些条件并进行分类讨论：(i) 如果条件成立，则可通过对偶误差界的结论证明 $B\ge 2D$ ; (ii) 如果条件不成立，那么利用具体不成立的条件可证明 $A,B,C$ 中的某一项大于等于 $2D$. 总之可证明 $(A+B+C)/2$ 是 ${\varphi }^t-{\varphi }^{t+1}$ 的一个下界，具体表达式如公式（3）所示.

利用势能函数的充分下降，可以证明算法具有 $O(1/{ϵ}^2)$ 的迭代复杂度.

定理1 记 $\{(x^t,y^t)\}$ 为本文中算法所生成的迭代序列. 如果上一节的两个假设成立，且参数 $p,\gamma ,c,\alpha$ 满足$p\ge 3L_f,\gamma \ge 0,c<1/(L_f+\gamma {\sigma }_{\max }^2(A)+p),\alpha <\frac{c(p-L_f{)}^2}{4{\sigma }_{\max }^2(A)},$ 此时存在 ${\beta }^{\prime }>0$, 使得对任意的 $\beta \le {\beta }^{\prime }$ 都有以下结论成立：

(1) $\{(x^t,y^t)\}$ 的每一个聚点都是问题 (1) 的 KKT 点；

(2) 对于 $ϵ>0$，算法能在 $O(1/{ϵ}^2)$ 次迭代中找到一个 $ϵ$-稳定点.

对于 $h_i(i=m+1,\cdots ,m+l)$ 都是线性函数的情形，对应的定理证明已在 [2] 中给出. 更进一步，本文给出了如下证明：

(1) 可证明 $\underline{f}$是 { ϕ t } \{\phi^t\} {ϕt} 的一个下界${}^{[3]}$. 结合引理1以及算法框架，可得

$$\underset{t\to \infty }{\lim }\Vert (x^{t+1},y^{t+1},z^{t+1})-(x^t,y^t,z^t)\Vert =0.$$

定义 $F(x,y,z)=(x^{+},y^{+},z^{+})$，其中 $(x^{+},y^{+},z^{+})$ 表示由算法生成的下一个迭代点. 由上式和 $F$ 的连续性，可证明 $\{(x^t,y^t,z^t)\}$ 的任意聚点 $(\bar{x},\bar{y},\bar{z})$ 都是 $F$ 的不动点，这说明 $(\bar{x},\bar{y})$ 是问题 (1) 的稳定点.

(2) 根据 ${\varphi }^t\ge \underline{f}$，可知对任意的 $t>0$，存在 s ∈ { 0 , ⋯ , t − 1 } s \in \{0,\cdots,t-1\} s∈{0,⋯,t−1} 使得 ${\varphi }^s-{\varphi }^{s+1}\le ({\varphi }^0-\underline{f})/t.$ 结合公式 (3) 可得$${\Vert x^s-x^{s+1}\Vert }^2<C/t,{\Vert Ax\left(y^{s+1},z^s\right)-b\Vert }^2<C/t,{\Vert x^{s+1}-z^s\Vert }^2<C/t,(4)$$

其中 $C$ 是适当的常数.

一方面，根据公式 (4) 以及原始误差界的理论可证明 $\Vert A{x}^{s+1}-b\Vert \le \sqrt{B_{1}C}/\sqrt{t}$，其中 $B_1$ 是适当的常数. 另一方面，根据算法具有性质
$$x^{s+1}=\arg \underset{x}{\min }\left\{⟨{\nabla }_{x}K\left(x^s,z^s;y^{s+1}\right),x-x^s⟩+\frac{1}{c}{\Vert x-x^s\Vert }^2+\iota (x)\right\},$$

可以借此找出一个$v$满足$v\in \nabla f\left(x^{s+1}\right)+A^T{y}^{s+1}+\partial \left(\iota \left(x^{s+1}\right)\right)$；对$v$表达式中的各项进行放缩，最终可得 $\Vert v\Vert \le \sqrt{B_{2}C}/\sqrt{t}$，其中 $B_2$ 是适当的常数. 因此可以看出 $(x^{s+1},y^{s+1})$ 是问题 (1) 的一个 $(\sqrt{B}/\sqrt{t})$-稳定点，其中 B = C max ⁡ { B 1 , B 2 } B = C\max\{B_1,B_2\} B=Cmax{B1​,B2​}. 收敛率即得证.

3.3 分块优化

考虑分块优化问题
$$\begin{array}{rl}& \min f(x_1,x_2,\cdots ,x_N)\\ \text{s.t. }& \sum _{i=1}^N{A}_i{x}_i=b,x_i\in {\mathcal{X}}_i,\end{array}(5)$$

其中${\mathcal{X}}_i$均为紧凸集. 定义 $x^t(i)=\left(x_1^{t+1},x_2^{t+1},\cdots ,x_{i-1}^{t+1},x_i^t,\cdots ,x_N^t\right)$，并用 $P_{{\mathcal{X}}_i}(\cdot )$ 表示到 ${\mathcal{X}}_i$ 的投影.

根据 2.2 节的算法，我们可以提出适合问题 (5) 的算法框架，并对其证明与定理1相同的收敛性结论. 在具体证明过程上，它与定理1的不同之处在于：(i) 在引理证明的第(1)步中，关于 $K(x^t,z^t;y^t)-K(x^{t+1},z^{t+1};y^{t+1})$ 下界的证明不同；（ii) 对于部分原始误差界结论的证明不同. 具体算法框架如下：

4. 数值实验

考虑问题
$$\underset{x}{\min }f(x):=\frac{1}{2}{x}^{T}Qx+r^{T}x\text{s.t. }Ax=b,\Vert x\Vert \le c,$$

其中 $Q\in {\mathbb{R}}^{n\times n}$ 是对称而未必半正定的矩阵，$r\in {\mathbb{R}}^n$, $A\in {\mathbb{R}}^{m\times n}$, $b\in {\mathbb{R}}^m$且 $c>0$.

定义 X = { x ∣ ∥ x ∥ ≤ c } \mathcal{X} = \{x ~|~ \|x\|\leq c\} X={x ∣ ∥x∥≤c} 以及它对应的指示函数$\iota (\cdot )$. 对任意的$(x,y)$，可以找到 $\nabla f(x)+A^{T}y+\partial \iota (x)$ 中范数最小的元素，不妨记作$v$. 结合$ϵ$-稳定点的定义，本节以 $\Vert v\Vert +\Vert Ax-b\Vert$ 的大小来衡量 $x$ 与稳定点的距离.

首先考察参数对本文算法的影响. 取 $m=20$, n = { 50 , 100 , 200 } n = \{50,100,200\} n={50,100,200}，固定的 $p,\gamma ,c,\alpha$ 及 β = { 0.05 , 0.2 , 0.5 } . \beta = \{0.05,0.2,0.5\}. β={0.05,0.2,0.5}.结果显示，对于不同规模的问题，较大的 $\beta$ 值都有助于算法的收敛.

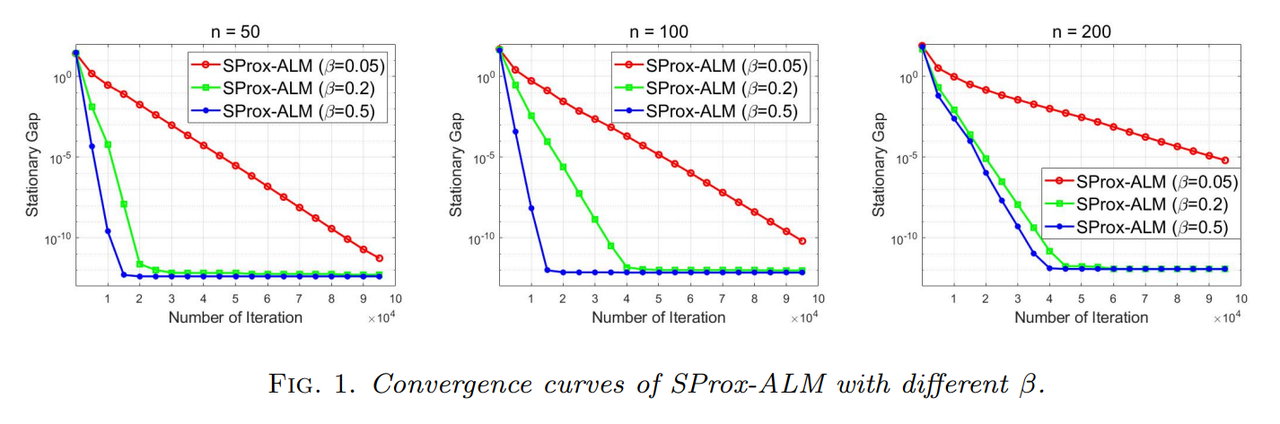
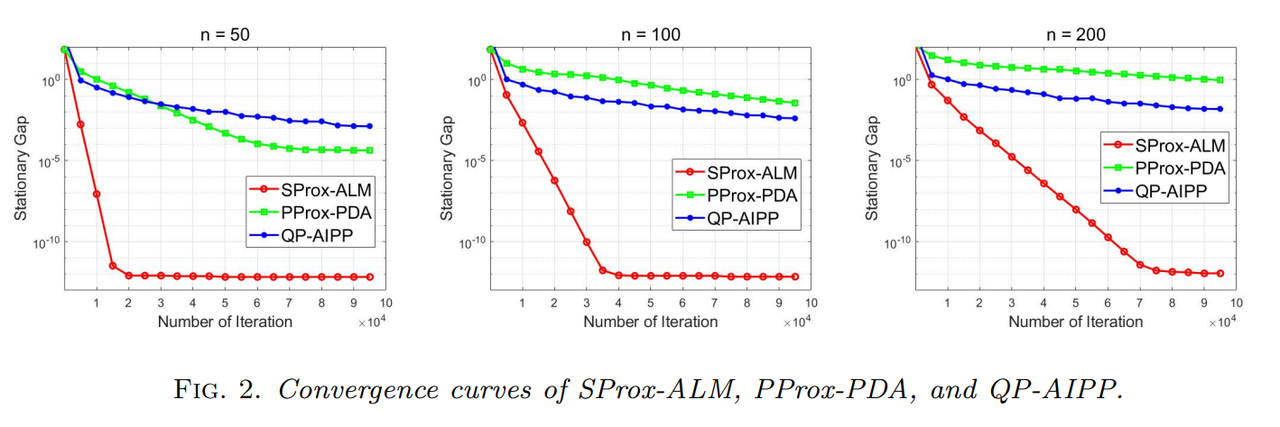
接下来将本文算法与其他方法进行比较. 在先前参数选择的基础上，固定 $\beta =0.2$. 将本文算法(SProx-ALM)、Pprox-PDA 算法${}^{[4]}$（Perturbed Proximal Primal-dual Algorithm）和 QP-AIPP 算法${}^{[5]}$（Quadratic Penalty Accelerated Inexact Proximal Point Method）进行比较. 结果显示，本文算法在 QP 问题的求解上具有更快的收敛速度.

参考文献

1. Zhang, Jiawei, Wenqiang Pu and Zhi-Quan Tom Luo. “On the Iteration Complexity of Smoothed Proximal ALM for Nonconvex Optimization Problem with Convex Constraints.” (2022).
2. Zhang, Jiawei and Zhi-Quan Tom Luo. “A Global Dual Error Bound and Its Application to the Analysis of Linearly Constrained Nonconvex Optimization.” SIAM J. Optim. 32 (2022): 2319-2346.
3. Zhang, Jiawei and Zhi-Quan Tom Luo. “A Proximal Alternating Direction Method of Multiplier for Linearly Constrained Nonconvex Minimization.” SIAM J. Optim. 30 (2018): 2272-2302.
4. Hajinezhad, Davood and Mingyi Hong. “Perturbed proximal primal–dual algorithm for nonconvex nonsmooth optimization.” Mathematical Programming 176 (2019): 207 - 245.
5. Kong, Weiwei, Jefferson G. Melo and Renato D. C. Monteiro. “Complexity of a Quadratic Penalty Accelerated Inexact Proximal Point Method for Solving Linearly Constrained Nonconvex Composite Programs.” SIAM J. Optim. 29 (2018): 2566-2593.

这篇关于优化｜复杂度分析——用于凸约束非凸优化问题的光滑化近似点增广拉格朗日算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---