本文主要是介绍拉格朗日乘数法什么时候考虑端点?解得的点是什么?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题提出
2013年的真题有一道题是用拉格朗日乘数法只能求出来一个点,当时很费解,因此查阅相关资料后,对这部分的知识做一个小总结。
无条件极值和条件极值
首先,在求无条件极值的时候,我们求的是曲面上的极值点。
例如:

这个A点就是无条件极值点。
而条件极值则是在原来曲面的基础上,由约束条件截得的曲线上的极值点。
例如:
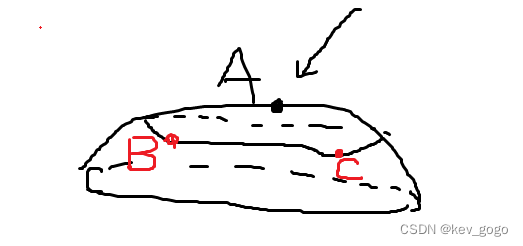
这里B点和C点就是条件极值点。
求最值
情况1:求边界上的最值时,直接用拉格朗日乘数法即可。
情况2:求区域内的最值时,用极值的充要条件求驻点即可。
情况3:求区域上的最值时(包含边界):1. 求驻点 2. 拉格朗日乘数法。
拉格朗日乘数法求的是什么?
拉格朗日乘数法实际上是将求条件极值的必要条件转化为了求无条件极值的必要条件。
用人话说就是求的是这个在约束条件下的曲线的驻点。
一般来说,驻点求完直接就是比较大小即可,但是2013年的这道题,求完只有一个点,因此引入端点问题。
什么时候需要考虑端点
看一元的情况下:
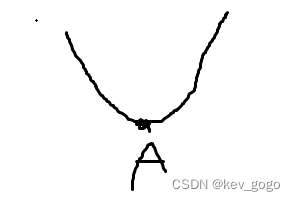
正常情况下,求得得驻点就是可能得极值点,这点A就是极小值,也是最小值。
然而:
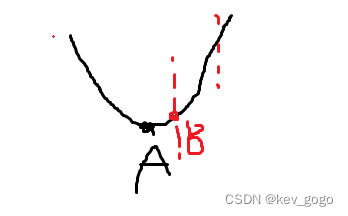
当我们划定一个范围后,最小值就变成B了,显然,这个点不是驻点。
而拉格朗日乘数法其实只能够求出来驻点,可能就是有遗漏了。
在二元的情况下:
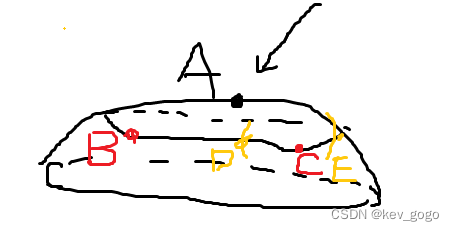
我规定了这个范围后,C当然也是极值点,那么和一元一样,这里我们除了驻点就还需要考虑端点的情况了,也就是D点和E点。
总结一下
当多元函数是光滑封闭曲线的时候不用考虑端点;
当多元函数被直线段或者曲线段(有时也会是平面(2016年数二真题))截得时需要考虑端点。
这篇关于拉格朗日乘数法什么时候考虑端点?解得的点是什么?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!