乘数专题
SVM中的拉格朗日乘数法和KKT条件的深入解析
在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法,对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值;如果含有不等式约束,可以应用KKT条件去求取。当然,这两个方法求得的结果只是必要条件,只有当是凸函数的情况下,才能保证是充分必要条件。KKT条件是拉格朗日乘子法的泛化。之前学习的时候,只知道直接应用两个方法,但是
乘数而上,创邻科技入选2024数商典型应用场景“乘数榜”
4月18日,由浙江省科学技术协会指导的2024未来数商大会在杭州成功举办。本次大会以“场景突破 乘数而上”为主题,国际国内数商共聚未来科技城学术交流中心,聚焦数据要素市场的制度创新、数据治理、场景应用与生态构建等话题展开研讨。 大会现场揭晓了2024数商典型应用场景“乘数榜”(下称“乘数榜”),并发布《2024数商产业场景调研报告》(下称“报告”)。创邻科技凭借着在数字金融领域的优秀表现和创新成
拉格朗日乘数法什么时候考虑端点?解得的点是什么?
问题提出 2013年的真题有一道题是用拉格朗日乘数法只能求出来一个点,当时很费解,因此查阅相关资料后,对这部分的知识做一个小总结。 无条件极值和条件极值 首先,在求无条件极值的时候,我们求的是曲面上的极值点。 例如: 这个A点就是无条件极值点。 而条件极值则是在原来曲面的基础上,由约束条件截得的曲线上的极值点。 例如: 这里B点和C点就是条件极值点。 求最值 情况1:求边界上的最值
【NOI2012】骑行川藏(拉格朗日乘数法)
传送门 l i m i t s : φ ( v 1 , v 2 , … , v n ) = ∑ k i ( v i − v i ′ ) 2 s i = E m i n i m i z e { f ( v 1 , v 2 , … , v n ) = ∑ s i v i } L ( v 1 , v 2 , … , v n ) = f + λ φ limits:\varphi(v_1,v_2,\do
保研数学问题复习-大数定理 中心极限定理 拉格朗日乘数法线代
离散 微积分 三个中值定理的区别、联系和物理意义(罗尔、拉格朗日、柯西) 线代 矩阵二次型 对于二次型,我们讨论的主要问题是:寻求可逆的线性变换,使二次型只含平方项(标准形)。如果标准形的系数只在1,-1,0三个数中取值,称为规范形。 用配方法化二次型成标准形 正定二次型 对称矩阵A为正定的充分必要条件是:A的各阶主子式都为正 在试验不变的条件下,重复试验多次,随机事件的
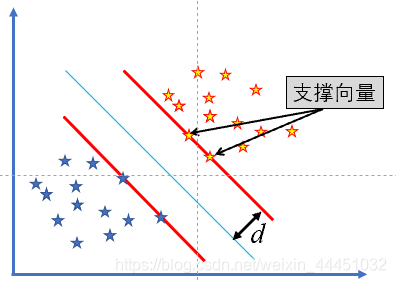
支持向量机SVM——最大间隔分离超平面的计算、拉格朗日乘数法求解不等式约束的优化问题
支持向量机SVM——最大间隔分离超平面的计算 如何定义两个集合的最优分隔超平面呢? 找到集合"边界"上的若干点,以这些点为基础计算超平面的方向,以二维坐标平面为例子 w T x + b = 0 w^Tx+b=0 wTx+b=0,当系数 w T w^T wT确定的时候,这个超平面的方向也就随之确定,以两个结果边界上的点的平均作为超平面的"截距"。 SVM线性分类问题 假设给定一个特征空
【观察】杉数科技:释放智能决策“乘数效应”,驱动智能制造高质量增长
毫无疑问,中国制造业在时代背景与国家政策的双重驱动下,正加速向数智化转型,而以数据驱动的智能决策也正成为制造业资源优化配置的“利器”,通过端到端的数据深度感知与决策优化,显然能够将工业和制造业的数据价值发挥到最大化。 确实如此,在Gartner对制造业运营数字化调查中,到2025年,70%在关键财务指标上优于竞争对手的上市公司也将以数据和分析为中心。同时IDC也预计,到2025年,超过60%的中
最小二乘和回归线、拉格朗日乘数、二元泰勒多项式、带约束变量的偏导数
33.最小二乘和回归线、拉格朗日乘数、二元泰勒多项式、带约束变量的偏导数 33. 最小二乘和回归线、拉格朗日乘数、二元泰勒多项式、带约束变量的偏导数33.1 最小二乘和回归线33.2 拉格朗日乘数(寻找受约束函数的极值)33.3 带两个约束条件的拉格朗日乘数33.4 二元泰勒多项式(为二元函数提供所有阶的多项式逼近)33.5 线性估计的误差公式33.6 带约束变量的偏导数 33.
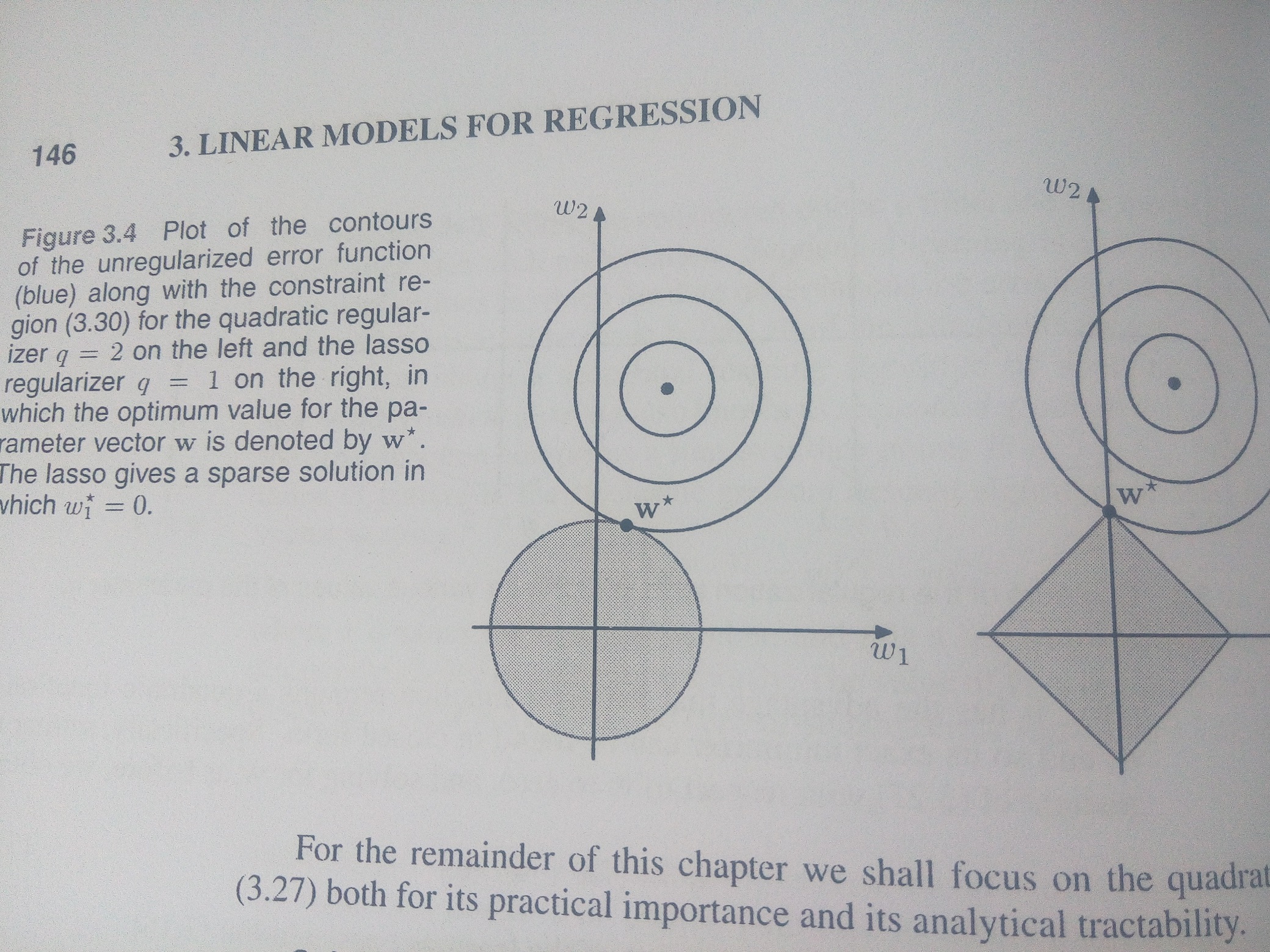
约束下的最优求解:拉格朗日乘数法和KKT条件
机器学习面对各种各样的求解极值或者最值问题 ,现在对常见的求解极值或者最值问题思路做一下理论上的梳理。 最值问题 简单了解最值问题 求最值是非常常见的问题,比如如何选择交通路线,最快地到达某地;如何用手头的钱买到分量最重的水果等等。 我们可以把需求定义为一个目标函数: f(x) f(x) 最值问题也就可以表示为 min[f(x)] min [ f(x) ] 对于一个