本文主要是介绍最小二乘和回归线、拉格朗日乘数、二元泰勒多项式、带约束变量的偏导数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
33.最小二乘和回归线、拉格朗日乘数、二元泰勒多项式、带约束变量的偏导数
- 33. 最小二乘和回归线、拉格朗日乘数、二元泰勒多项式、带约束变量的偏导数
- 33.1 最小二乘和回归线
- 33.2 拉格朗日乘数(寻找受约束函数的极值)
- 33.3 带两个约束条件的拉格朗日乘数
- 33.4 二元泰勒多项式(为二元函数提供所有阶的多项式逼近)
- 33.5 线性估计的误差公式
- 33.6 带约束变量的偏导数
33. 最小二乘和回归线、拉格朗日乘数、二元泰勒多项式、带约束变量的偏导数
33.1 最小二乘和回归线

33.2 拉格朗日乘数(寻找受约束函数的极值)
有时我们需要找到一个函数的极值,这个函数的定义域被限定在平面的某个特定子集内,例如,一个圆形区域,一个封闭的三角形区域,或者沿着一条曲线。

例1:




例2:





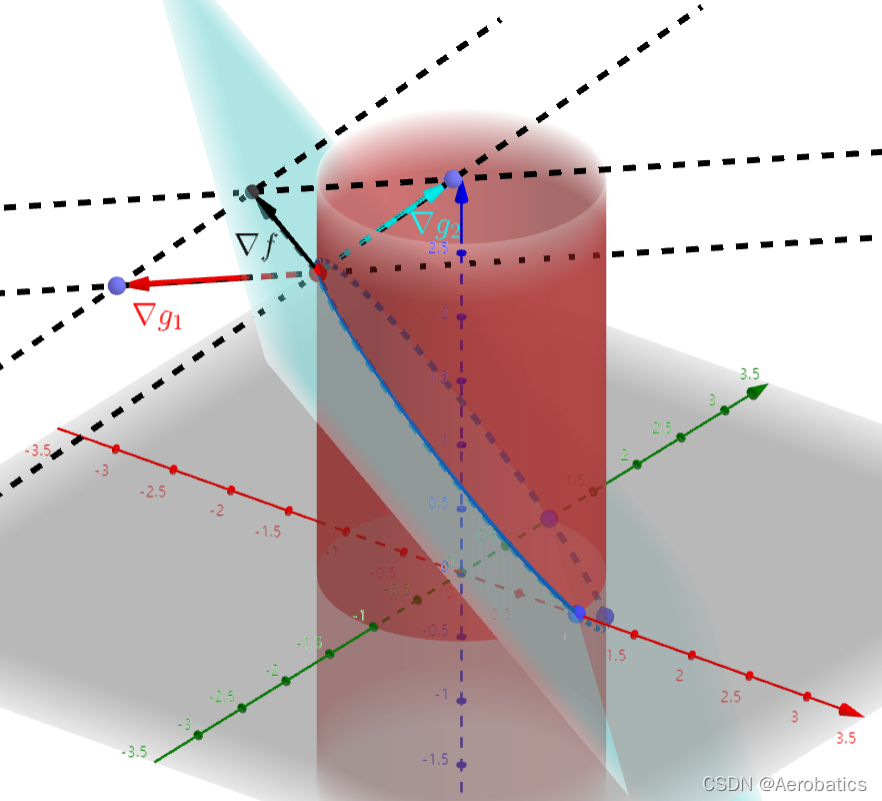
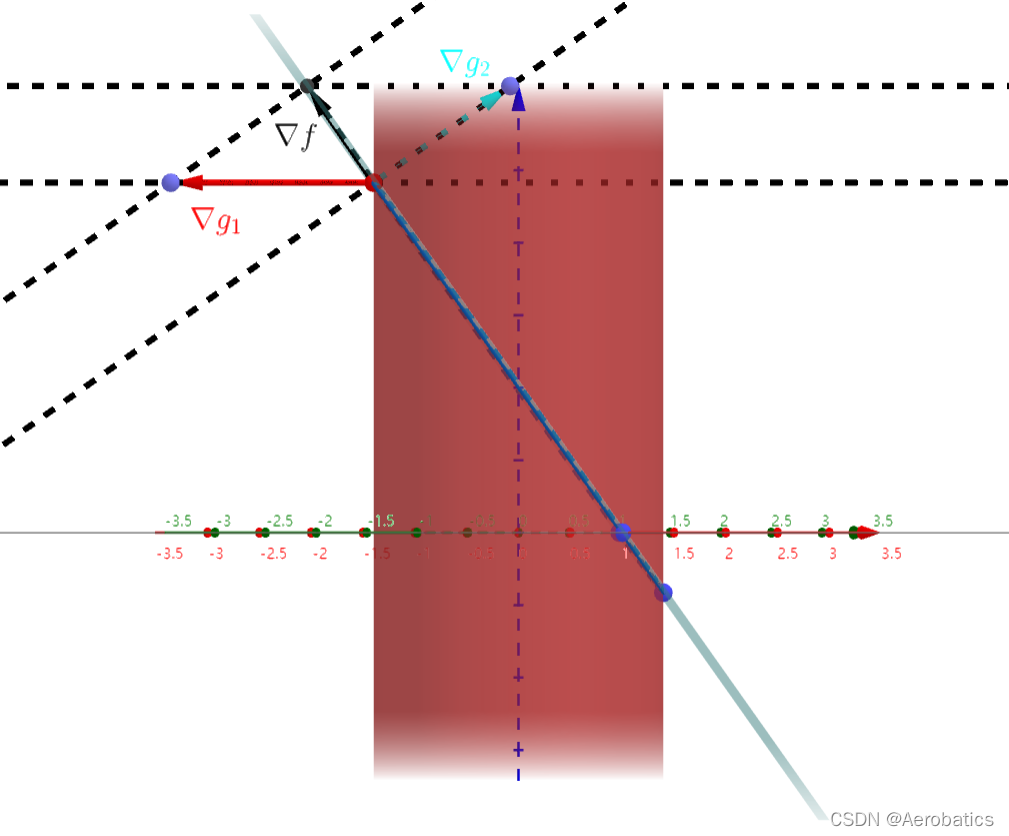
33.3 带两个约束条件的拉格朗日乘数
许多问题要求我们找到可导函数 f ( x , y , z ) f(x,y,z) f(x,y,z) 的极值,这个可导函数受两个约束条件:
g 1 ( x , y , z ) = 0 、 g 2 ( x , y , z ) = 0 g_1(x,y,z)=0、g_2(x,y,z)=0 g1(x,y,z)=0、g2(x,y,z)=0


例子:

33.4 二元泰勒多项式(为二元函数提供所有阶的多项式逼近)
二阶导数判别法的推导


33.5 线性估计的误差公式

例子:

33.6 带约束变量的偏导数
决定哪些变量是自变量,哪些变量是因变量
例子:

当函数 w = f ( x , y , z ) w=f(x,y,z) w=f(x,y,z) 中的变量被另一个方程约束时,如何找到 ∂ w ∂ x \frac{\partial w}{\partial x} ∂x∂w

例1:

例2:

这篇关于最小二乘和回归线、拉格朗日乘数、二元泰勒多项式、带约束变量的偏导数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


