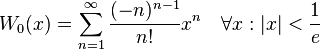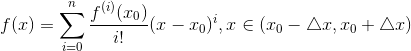泰勒专题
漫步数学分析三十六——泰勒定理
我们讨论一般函数 f:A⊂Rn→Rm f:A\subset R^n\to R^m的泰勒公式,为此我们首先讨论高阶导数。对于 f:Rn→R f:R^n\to R,定义高阶偏导没有问题;我们仅仅迭代偏导的过程 ∂2f∂x1∂x2=∂∂x1(∂∂x2f) \frac{\partial^2f}{\partial x_1\partial x_2}=\frac{\partial}{\parti
用泰勒级数展开证明欧拉公式
原址 欧拉公式非常简明的证明,欧拉公式是宇宙给人类的礼物,非常感谢麻省理工Gilbert strang教授! 第一次写博客,不知道怎么上传pdf文档,见谅。
(泰勒展开式/欧拉公式)证明:e^x推导及e^(iπ) = -1展开过程
欧拉公式意义:欧拉公式是在复分析领域的公式,将三角函数与复数指数函数相关联,因其提出者莱昂哈德·欧拉而得名.1.将指数函数ex展开成幂级数形式。首先,假设有恒等式:e^x= a0 + a1x + a2x^2 + a3x^3 + a4x^4 + …+ anx^n(n趋向无穷大)两侧取导数:e^x = 0 + a1 + 2a2x + 3a3x^2 + 4a4x^3 + …+ nanx^(n-1
泰勒级数定义及相关展开式
泰勒级数、欧拉公式、三角函数 泰勒级数的定义: 若函数f(x)在点的某一临域内具有直到(n+1)阶导数,则在该邻域内f(x)的n阶泰勒公式为: 其中:,称为拉格朗日余项。 以上函数展开式称为泰勒级数。 泰勒级数在幂级数展开中的作用: 在泰勒公式中,取,得: 这个级数称为麦克劳林级数。函数f(x)的麦克劳林级数是x的幂级数,那么这种展开是唯一的,且必然与f(x)的麦克劳
泰勒创造力达到顶峰?(上)
hello,大家好!今天看一篇经济学人的一篇评论,说的是泰勒·斯威夫特当前的创造力。经济学人总是语不惊人死不休,看看它对这位音乐天才做了怎样的评价。 事先声明哈,本文就是一种英语学习类讲述,没带任何个人色彩,都是文章散发出的气息。 Has Taylor Swift peaked? 泰勒·斯威夫特已经达到顶峰了么?
泰勒创造力达到顶峰?(下)
上文说了一半,回顾看文: https://blog.csdn.net/weixin_41953346/article/details/138336524 继续看下文 “Like I lost my twin /Fuck it if I can't have him,"she sings in “Down Bad".
泰勒公式--char4
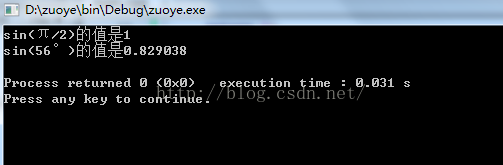
编程实现泰勒公式:求出sin(π/2)、sin(56°)、cos(87°)、cos(π/3) 一点说明:数学库(#include<Cmath>)中已经提供了sin和cos函数,一般解题中我们直接调用即可,而本题要求自定义函数实现,为区别起见,分别起名为mysin和mycos。 提示和要求:(1)要求自定义函数要写在main函数之后;(2)自定义函数中求解的效率问题必须考虑(用好迭代
浅谈泰勒公式与麦克劳林公式
一.预备知识: 1.高阶无穷小 2.高阶无穷小的运算 二.泰勒公式与麦克劳林公式 1.泰勒公式 2.麦克劳林公式 应用1:计算x->0时的极限 展开到几阶? 等价无穷小替换规则
UVa 113 / POJ 2109 Power of Cryptography (使用double处理大整数泰勒公式与误差分析)
113 - Power of Cryptography Time limit: 3.000 seconds http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=99&page=show_problem&problem=49 http://poj.org/problem?id=2109
泰勒法计算sin和cos值
#include <stdio.h> #define pie 3.14 double myabs(double n); double mysin(double x); double mycos(double x); main() { int choose; double result,jiaodu; while(1) { printf("************\n"
太乐了(泰勒展示求sin值)
/* *Copyright(c)2014,烟台大学计算机与控制工程学院 *All rights reserved. *文件名称:zuoye.cpp *作 者:隋文韬 *完成日期:2016年3月25日 *版 本 号:v1.0 * *问题描述:用sin泰勒展示编写程序,求出sin(π/2)和sin(56°)的值。 *输入描述:无输入值。
学习笔记:用c语言编写泰勒展开公式myexp()实现math.h.数学函数库中的exp()函数。并与exp()函数做比较。精度相同。
学习笔记:用c语言编写泰勒展开公式myexp()实现math.h.数学函数库中的exp()函数。并与exp()函数做比较。精度相同。 #include <stdio.h>#include <math.h>double myexp(double x){int i,k,m,t;int xm=(int)x; double sum;double e ;double ef;double z ;doub
数学笔记31——幂级数和泰勒级数
实际应用中,总是会出现一堆复杂的函数,这类函数往往令物理学家和数学家都十分头疼。为了解决这一窘境,泰勒想:会不会存在一种方法,把一切函数表达式都转化为多项式函数来近似呢?这样,处理问题不就变得简单了吗?经过泰勒夜以继日的奋斗,终于研究出了泰勒级数的理论。它将一切函数,不论表达式有多么多么的复杂,只有能保证n阶导数存在,就能将它的局部用多项式展开。泰勒级数在近似计算中有重要作用。实际上,利用多项
GBDT原理与泰勒展开
11.13 https://www.zhihu.com/question/41354392/answer/98658997 https://zhuanlan.zhihu.com/p/50176849
泰勒展开的理解,以及在使用泰勒公式进行估算时,在不同点展开的区别和意义是啥?
泰勒展开:用多项式函数(或称为幂级数)来拟合一个无限可导的复杂函数,使该复杂函数能以简单的方式计算。 泰勒展开面临一个问题,要在某一个点的位置展开,即上面提到的 。展开点的意义是什么?如何选择合适的展开点呢? 展开点的含义是什么呢? 泰勒级数展开是用一个多项式函数来拟合一个复杂函数,但只能拟合这个复杂函数的局部区域,超过这个区域的拟合误差会很大。该局部区域在什么位置呢?没错,就是在展开点
浅显易懂——泰勒展开式
第一次见到泰勒展开式的时候,我是崩溃的。泰勒公式长这样: 好奇泰勒是怎么想出来的,我想,得尽量还原公式发明的过程才能很好的理解它。 首先得问一个问题:泰勒当年为什么要发明这条公式? 因为当时数学界对简单函数的研究和应用已经趋于成熟,而复杂函数,比如:这种一看就头疼的函数,还有那种根本就找不到表达式的曲线。除了代入一个x可以得到它的y,就啥事都很难干了。所以泰勒同学就迎难而上!决定让这些式
图文证明 泰勒公式展开
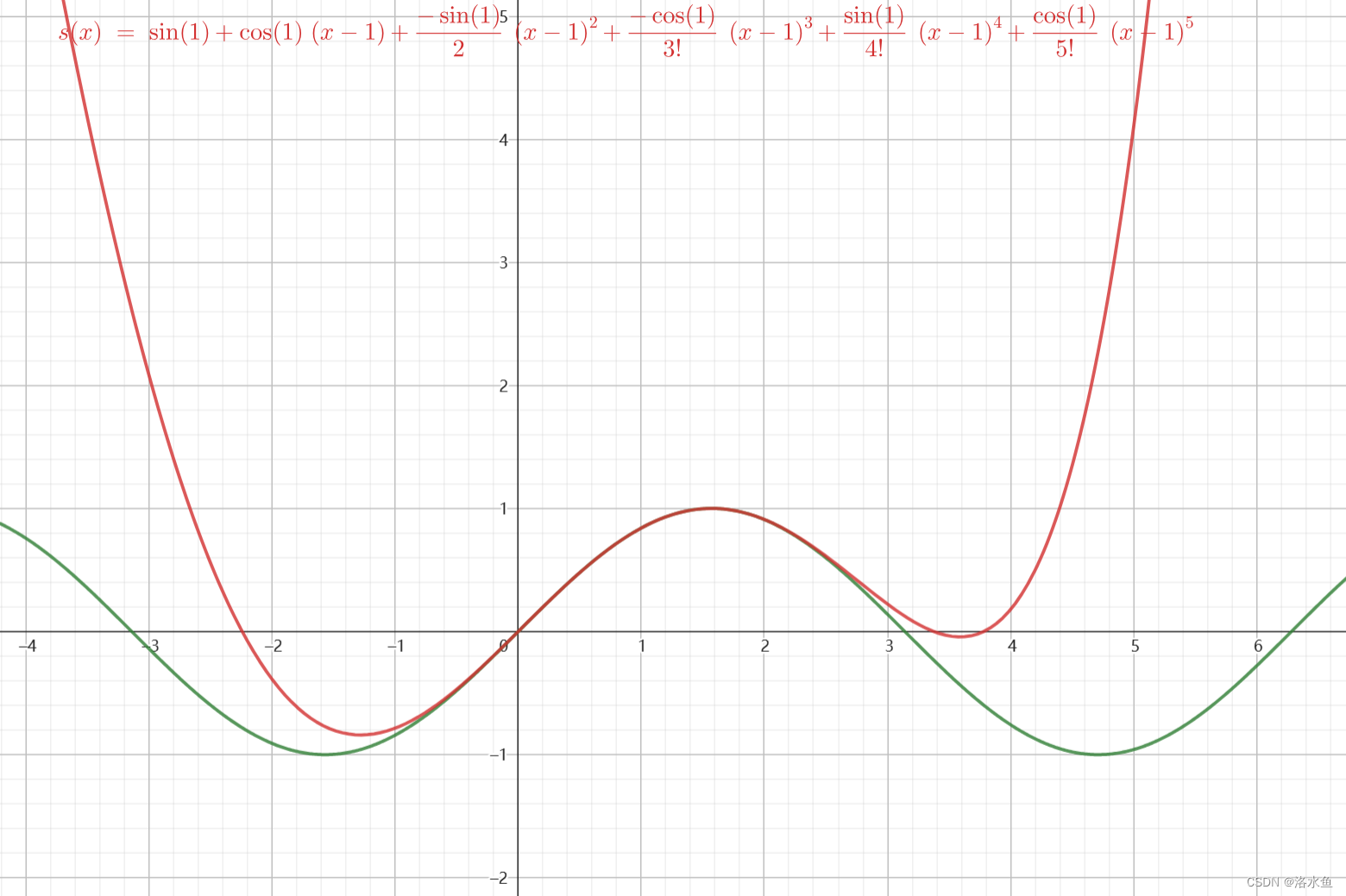
泰勒公式 泰勒公式简单来说就是,可以用一个N次多项式来表示出一个连续可导的函数 f(x) 是一个用函数在某点的信息描述其附近取值的公式 第一步 思考 这是一个sin(x)的图像 用函数在原点的信息描述其附近取值 用一阶导数贴合: 直接用切线来贴合就好 画一个点(0,sin(0)除的切线 可以由直线的两点式得 : y = f ( 0 ) + f ′ ( 0 ) ( x − 0 ) y =
高等数学:分母阶数未知,如何对分子进行泰勒展开?——对泰勒公式展开阶数问题的分析
分母阶数未知,如何对分子进行泰勒展开?——对泰勒公式展开阶数问题的分析 关于对泰勒公式的基本理解,阅读我的另一篇博客:如何理解泰勒展开公式?等价无穷小与泰勒公式的关系是什么? 题源:《1800题》P79 64题
xgboost兼具线性规模求解器和树学习算法,GBDT 方法只利用了一阶的导数信息,Xgboost 则是对损失函 数做了二阶的泰勒展开,并在目标函数之外加入了正 则项,整体求最优解,用于权衡目标函数的
Xgboost 是华盛顿大学陈天奇于 2016 年开发的 Boosting 库,兼具线性规模求解器和树学习算法[14]。 它是 GBDT 算法上的改进,更加高效。传统的 GBDT 方法只利用了一阶的导数信息,Xgboost 则是对损失函 数做了二阶的泰勒展开,并在目标函数之外加入了正 则项,整体求最优解,用于权衡目标函数的下降和模型 的复杂程度,避免过拟合,提高模型的求解效率,其步 骤如下: (
【转】利用泰勒公式推导梯度下降法
原作者: 红色石头 | 来自: AI有道 梯度下降 算法的公式非常简单,”沿着梯度的反方向(坡度最陡)“是我们日常经验得到的,其本质的原因到底是什么呢?为什么局部下降最快的方向就是梯度的负方向呢?也许很多朋友还不太清楚。没关系,接下来我将以通俗的语言来详细解释梯度下降算法公式的数学推导过程。 下山问题 假设我们位于黄山的某个山腰处,山势连绵不绝,不知道怎么下山。于是决定走
泰勒展开-一个点是如何蕴含整个世界
看过《三体》的童鞋应该对云天明讲的三个寓言很有印象,其中关于针眼画师的那个尤其精彩。 泰勒公式浅谈原理(转) 为什么可以从一个单独的点不断求导就可以画出整个函数的曲线?即“一点是如何蕴含整个世界”的。 https://blog.csdn.net/qq_38906523/article/details/79851654https://blog.csdn.net/SoHardToNamed/ar