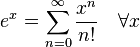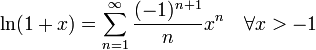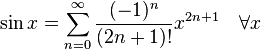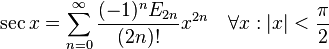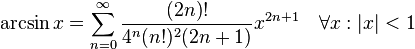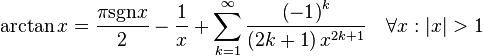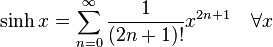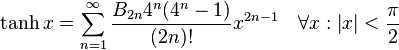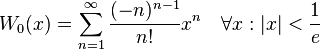泰勒级数定义及相关展开式

若函数f（x）在点的某一临域内具有直到（n+1）阶导数，则在该邻域内f（x）的n阶泰勒公式为：

其中：，称为拉格朗日余项。

以上函数展开式称为泰勒级数。

泰勒级数在幂级数展开中的作用：

在泰勒公式中，取，得：

这个级数称为麦克劳林级数。函数f（x）的麦克劳林级数是x的幂级数，那么这种展开是唯一的，且必然与f（x）的麦克劳林级数一致。

注意：如果f（x）的麦克劳林级数在点的某一临域内收敛，它不一定收敛于f（x）。因此，如果f（x）在处有各阶导数，则f（x）的麦克劳林级数虽然能做出来，但这个级数能否在某个区域内收敛，以及是否收敛于f（x）都需要进一步验证。

几个重要的泰勒级数。参数x 为复数时它们依然成立。

• 指数函数和自然对数:

• 几何级数:

• 二项式定理:

• 三角函数:

• 双曲函数:

• 朗伯W函数:

二项式展开中的C(α,n)是二项式系数。

tan(x)和tanh(x)展开式中的Bk是伯努利数。

sec(x)展开式中的Ek是欧拉数。