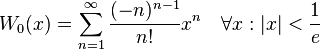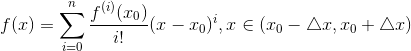在 Matlab 中，没有专门求傅氏级数的函数调用，但我们可编写一个函数来求 f (x)在 [-l,l]上的 Fourier 级数． 打开 Matlab 的 M 文件编辑窗口，输入如下命令行：  function [A,B,F]=fseries(f,x,n,a,b)  if nargin==3,a=-pi;b=pi;end  L=(b-a)/2;  if a+b~=0,f=subs(f,x,x+L

X=an*(n-1)!+an-1*(n-2)!+...+ai*(i-1)!+...+a2*1!+a1*0! 其中，a为整数，并且0<=ai<i(1<=i<=n)。这就是康托展开。康托展开可用代码实现。 康托展开的应用实例： {1,2,3,4,...,n}表示1,2,3,...,n的排列 如 {1,2,3} 按从小到大排列一共6个。123 132 213 231 312 321 。 　　代表的

欧拉公式意义：欧拉公式是在复分析领域的公式,将三角函数与复数指数函数相关联，因其提出者莱昂哈德·欧拉而得名.1.将指数函数ex展开成幂级数形式。首先，假设有恒等式：e^x= a0 + a1x + a2x^2 + a3x^3 + a4x^4 + …+ anx^n（n趋向无穷大）两侧取导数：e^x = 0 + a1 + 2a2x + 3a3x^2 + 4a4x^3 + …+ nanx^(n-1

泰勒级数、欧拉公式、三角函数 泰勒级数的定义： 若函数f（x）在点的某一临域内具有直到（n+1）阶导数，则在该邻域内f（x）的n阶泰勒公式为： 其中：，称为拉格朗日余项。 以上函数展开式称为泰勒级数。 泰勒级数在幂级数展开中的作用： 在泰勒公式中，取，得： 这个级数称为麦克劳林级数。函数f（x）的麦克劳林级数是x的幂级数，那么这种展开是唯一的，且必然与f（x）的麦克劳

康托展开式： X=an(n-1)!+(an-1)(n-2)!+…+ai(i-1)!+…+a2*1!+a1*0! （解决一些序列问题的算法）* 　　 其中，ai为当前未出现的元素中是排在第几个（从0开始）。这个公式可能看着让人头大，最好举个例子来说明一下。例如，有一个数组 s = ["A", "B", "C", "D"]，它的一个排列 s1 = ["D", "B", "A", "C"]，现在

第一次见到泰勒展开式的时候，我是崩溃的。泰勒公式长这样： 好奇泰勒是怎么想出来的，我想，得尽量还原公式发明的过程才能很好的理解它。 首先得问一个问题：泰勒当年为什么要发明这条公式？ 因为当时数学界对简单函数的研究和应用已经趋于成熟，而复杂函数，比如：这种一看就头疼的函数，还有那种根本就找不到表达式的曲线。除了代入一个x可以得到它的y，就啥事都很难干了。所以泰勒同学就迎难而上！决定让这些式

本文讲的是[译]如何在 iOS 上实现类似 Airbnb 中的可展开式菜单， 原文地址：How to implement expandable menu on iOS (like in Airbnb) 原文作者：Evgeny Matviyenko 译文出自：掘金翻译计划 本文永久链接：github.com/xitu/gold-m… 译者：RichardLeeH 校对者：iOSleep