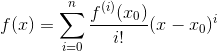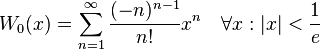浅显易懂——泰勒展开式

本文主要是介绍浅显易懂——泰勒展开式，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第一次见到泰勒展开式的时候，我是崩溃的。泰勒公式长这样：

好奇泰勒是怎么想出来的，我想，得尽量还原公式发明的过程才能很好的理解它。

首先得问一个问题：泰勒当年为什么要发明这条公式？

因为当时数学界对简单函数的研究和应用已经趋于成熟，而复杂函数，比如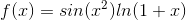：这种一看就头疼的函数，还有那种根本就找不到表达式的曲线。除了代入一个x可以得到它的y，就啥事都很难干了。所以泰勒同学就迎难而上！决定让这些式子统统现出原形，统统变简单。

让我们沿着泰勒同学（假装泰勒是这么想的）的思路来：

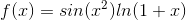
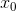
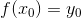
要让一个复杂函数变简单，能不能把它转换成别的表达式？比如函数，怎么看都看不出思路，怎么办呢？我们先不要一口吃掉它，可以先从它最小的部分算起，比如说一个点。可以得到：。暂时看不出有什么规律。

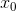
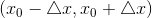
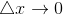
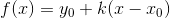
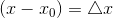
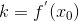
那就继续增大研究的对象，比如说的领域，。可以得到：，其中，。好像还是看不出什么规律？然鹅，聪明的泰勒早以看穿一切。

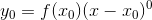
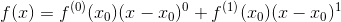
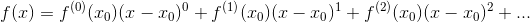
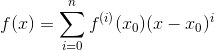
因为，所以原式可以化为：。所以泰勒想是不是这样：，即。嗯先假设是这样，然后泰勒同学决定验证一下。

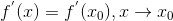
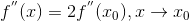
先求个导试试：。对了，泰勒同学很激动！继续求：，咦，不对了。那说明有了一些问题。仔细分析一下问题在哪呢？

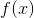
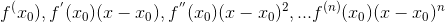
我们可以尝试把拆开来：，然后分析他们之间有什么共性。

让我们对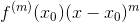进行求导看看：

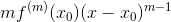
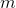
一阶导：，嗯多了个。

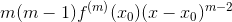
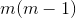
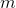
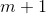
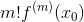
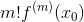
二阶导：，多了。好像有点规律了，

......

阶导：

阶导：0。是一个常数，所以对求导就是0了。

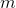
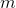
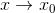
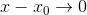
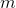
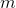
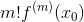
这里规律很明显了，阶导以后都是0！但是阶导以前呢？还是蛮复杂的，不过不用担心，因为，即，所以阶导以前也都是0，而阶导就是。perfect！

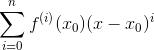
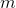
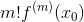
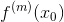
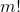
这样就很清晰了：对求阶导为。但是我们想要的值是，那就把给除掉！

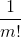
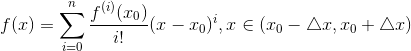
即乘于一个，所以，证明完毕。泰勒同学很开心！

这篇关于浅显易懂——泰勒展开式的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---