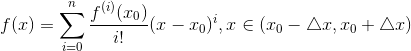Cantor展开式

本文主要是介绍Cantor展开式，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

X=an*(n-1)!+an-1*(n-2)!+...+ai*(i-1)!+...+a2*1!+a1*0! 其中，a为整数，并且0<=ai<i(1<=i<=n)。这就是康托展开。康托展开可用代码实现。

康托展开的应用实例：

{1,2,3,4,...,n}表示1,2,3,...,n的排列 如 {1,2,3} 按从小到大排列一共6个。123 132 213 231 312 321 。
　　代表的数字 1 2 3 4 5 6 也就是把10进制数与一个排列对应起来。
　　他们间的对应关系可由康托展开来找到。
　　如我想知道321是{1,2,3}中第几个大的排列可以这样考虑 ：
　　第一位是3，当第一位的数小于3时，那排列数小于321 如 123、 213 ，小于3的数有1、2 。所以有2*2!个。再看小于第二位2的：小于2的数只有一个就是1 ，所以有1*1!=1 所以小于321的{1,2,3}排列数有2*2!+1*1!=5个。所以321是第6个大的数。 2*2!+1*1!+1*0!就是康托展开。
　　再举个例子：1324是{1,2,3,4}排列数中第几个大的数：第一位是1小于1的数没有，是0个 0*3! 第二位是3小于3的数有1和2，但1已经在第一位了，所以只有一个数2 1*2! 。第三位是2小于2的数是1，但1在第一位，所以有0个数 0*1! ，所以比1324小的排列有0*3!+1*2!+0*1!=2个，1324是第三个大数。

 

#include <iostream>
#include <string>
using namespace std;const int SIZE    = 12;
const string END  = "-1";
int factory[SIZE] = { 0, 1, 2, 6, 24, 120,720, 5040, 40320, 362880, 3628800,39916800 }; int main(){int pos = 0;string val;while( true ){pos = 0;cin >> val;if( val == END ) break;const int size = val.length();for( int i = 0; i < val.length(); ++i ){int count = 0;for( int j = i + 1; j < val.length(); ++j ){if( val[i] > val[j] )count++;}pos += count * factory[size - i - 1];}cout << val << " is in the position of : " << pos + 1 << endl;}return 0;}

这篇关于Cantor展开式的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---