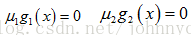kkt专题
SVM中的拉格朗日乘数法和KKT条件的深入解析
在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法,对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值;如果含有不等式约束,可以应用KKT条件去求取。当然,这两个方法求得的结果只是必要条件,只有当是凸函数的情况下,才能保证是充分必要条件。KKT条件是拉格朗日乘子法的泛化。之前学习的时候,只知道直接应用两个方法,但是
Lingo学习—— 拉格朗日乘子法 KKT条件
目录 一、初识拉格朗日乘子法和KKT条件 什么是拉格朗日乘子法? 二、最优化问题会碰到一下三种情况: (1)无约束条件 (2)等式约束条件 例题1.1:求椭球内接长方体 的最大体积。 例题1.2:(用LINGO求解)求原点到椭圆的最短距离。 (3)不等式约束条件 参考文章:(如侵权,请联系我删除) 一、
SVM中KKT条件介绍
KKT条件介绍 最近学习的时候用到了最优化理论,但是我没有多少这方面的理论基础。于是翻了很多大神的博客把容易理解的内容记载到这篇博客中。因此这是篇汇总博客,不算是全部原创,但是基础理论,应该也都差不多吧。因才疏学浅,有纰漏的地方恳请指出。 KKT条件是解决最优化问题的时用到的一种方法。我们这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最
手推支持向量机03-硬间隔SVM-模型求解(对偶问题之KKT条件)
目录 1.写在前面 2.KTT条件 3.求最终的w*,b*和最终的决策函数 1.写在前面 上面我们讲到了怎么对硬间隔SVM进行求解,我们我们先把带约束问题,转化为无约束问题,通过强对偶关系将minmax转为maxmin,对w,b求min,最终我们求出来最小值,然后关于λ求最大值。 我们最后圈出来的地方,可以变成min,只需要在后面加上符号。因为习
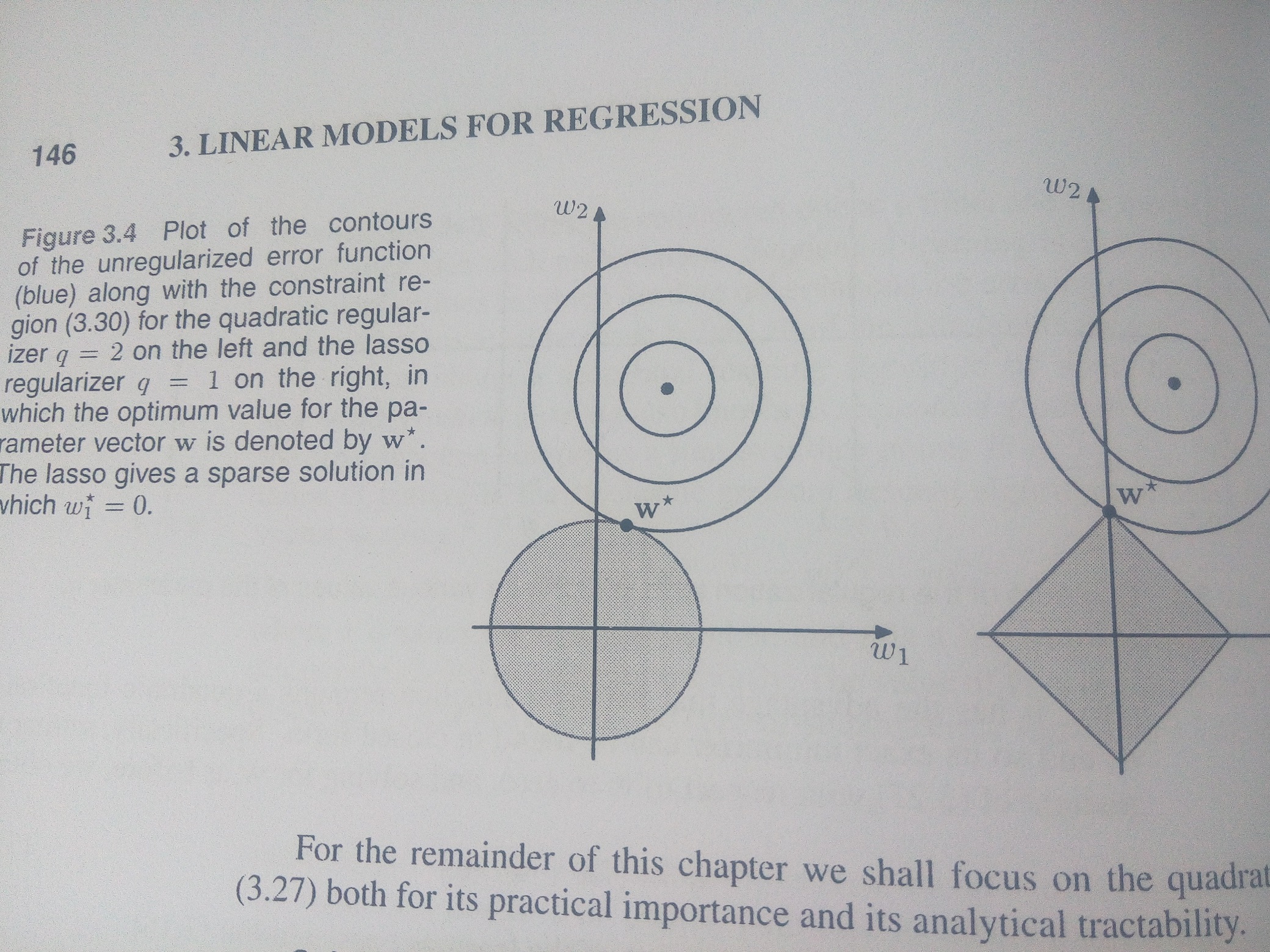
从L1,L2正则,到KKT条件下的拉格朗日乘法到拉格朗日对偶问题
转:相对清晰的一篇博客 从loss的l1,l2正则,追溯到模型复杂度衡量,追溯到不等式极值问题,以下两篇文章,可以进一步深入了解背后的数学原理 L1、L2正则化和过拟合 [从KKT条件下的拉格朗日乘法到拉格朗日对偶问题]
svm的对偶,kkt,拉格朗日乘子法
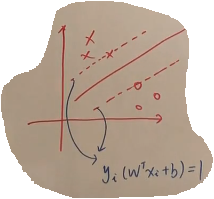
原文链接:https://blog.csdn.net/bit_666/article/details/79865225 1.SVM基础模型 给定训练集D={(x1,y1),(x2,y2)...(xn,yn)},yi∈{-1,1},例如下面图中的点,蓝线左上方的6个点对应1类,右下方的6个点对应-1类,基于数据分类的思想,如果我们想把两类数据分开,显然蓝线不是唯一的选择,我们有无数条直线可以选择
约束极值问题之拉格朗日乘子法、KKT条件与对偶理论
文章目录 1 等式约束极值问题1.1 拉格朗日乘子法(必要条件) 2 不等式约束极值问题2.1 约束作用2.2 不等式约束的几何解释2.3 下降方向2.4 可行方向2.5 Fritz John条件(最优解必要条件)2.6 Kuhn-Tucker条件(最优解必要条件 - 约束规格)2.7 最优解必要条件 3 对偶问题3.1 原始问题的等价问题3.2 原始问题的对偶问题3.3 原始问题与对偶问题
理解拉格朗日乘子法与KKT条件
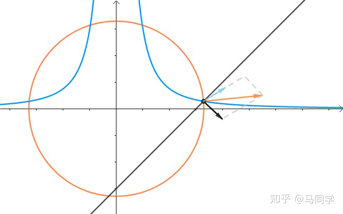
理解拉格朗日乘子法与KKT条件 拉格朗日乘子法 https://www.matongxue.com/madocs/939.html 看完小结: 对于曲线 z1=x2+y2 和曲线 z2=y*(x**2) 。z2=3时,在两曲线的相切点,两曲线的梯度向量平行 拉格朗日法与KKT条件 https://mp.weixin.qq.com/s/SnHGG7ZEZ9SJapPmWhhHpQ 注意图
人工智能_机器学习065_SVM支持向量机KKT条件_深度理解KKT条件下的损失函数求解过程_公式详细推导_---人工智能工作笔记0105
之前我们已经说了KKT条件,其实就是用来解决 如何实现对,不等式条件下的,目标函数的求解问题,之前我们说的拉格朗日乘数法,是用来对 等式条件下的目标函数进行求解. KKT条件是这样做的,添加了一个阿尔法平方对吧,这个阿尔法平方肯定是大于0的,那么 可以结合下面的文章去看,也就是说,如果我们要求: 函数在比如h(x)<=0的条件下的解,那么我们就可以添加一个阿尔法的平方,让这个阿尔
人工智能_机器学习061_KKT条件公式理解_原理深度解析_松弛变量_不等式约束---人工智能工作笔记0101
然后我们再来看,前面我们,拉格朗日乘子法,把带有条件的,问题,优化成了等式问题,从而, 构建拉格朗日乘子公式,进行实现了求解,但是在现实生活中,往往也有,很多不等式问题. 比如上面的这个,就是要求是h(x)<=0的情况下,函数f(x)的最小值. 可以看到,这个带有一个不等式的条件,那么这种的如何求呢 我们可以回去看看拉格朗日乘子法的公式,可以看到是一个等式条件,这个时候可以,引
约束优化之Lagrange乘子法KKT条件对偶问题最容易理解解读
1.无约束优化的常用方法 在讲带约束优化方法之前,我们先简单回顾一下常用的无约束优化方法。 1.梯度下降法 2.牛顿法/拟牛顿法 3.共轭梯度法 … 上面梯度系列的无约束条件下的最优化,基本解法是根据极值的必要条件一阶导数为0,通过泰勒展开等形式,构造不同数列不断逼近最优解。 2.带约束的优化 实际情况中,不带约束的场景比较少见,大部分都为带约束的优化问题。看一个大家都用的图: 上图中,
理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
转自(http://blog.csdn.net/xianlingmao/article/details/7919597) 在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法,对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值;如果含有不等式约束,可以应用KKT条件去求取。当然,这两个方法求得的结果只是必要条件,
机器学习之拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法,对于等式约束的优化问题,可以应用拉格朗日乘子法去求取最优值;如果含有不等式约束,可以应用KKT条件去求取。当然,这两个方法求得的结果只是必要条件,只有当是凸函数的情况下,才能保证是充分必要条件。KKT条件是拉格朗日乘子法的泛化。之前学习的时候,只知道直接应用两个方法,但是却
Lagrange与KKT的简易解释
本文将以梯度下降法的方式来解释Lagrange和KKT。 关键词:梯度下降法、等高线 基础定义 Lagrange 求解等式约束下的最优化问题 Lagrange函数: (1) 方程组的解是原问题的可能的最优解 KKT 求解不等式约束下的最优化问题 Lagrange函数: (2) 方程组,即KKT条件,的解是原问题的可能的最优解 解释 梯度的定义 , 等式约束 因
手推机器学习系列笔记——手推SVM(1)硬间隔、软间隔、约束优化问题、对偶性证明、KKT条件
笔记是听了b站大神的白板推导机器学习系列课,再结合李航老师的《统计学习方法》、周志华老师的西瓜书以及其他优秀博主的博客而成(浑然天成!!!): https://space.bilibili.com/97068901?from=search&seid=9183191776664110144(大神的白板推导机器学习系列课传送门) 对于大神的课,我只能说太强了,讲的特别特别好!下面让我们开始吧!
复盘:手推SVM支持向量机二分类超平面,求解目标函数原问题,kkt条件,对偶问题求q,核函数、hinge loss损失函数,硬间隔,软间隔,最后得到w和b
复盘:手推SVM支持向量机二分类超平面,求解目标函数原问题,kkt条件,对偶问题求q,核函数、hinge loss损失函数,硬间隔,软间隔,最后得到w和b 提示:系列被面试官问的问题,我自己当时不会,所以下来自己复盘一下,认真学习和总结,以应对未来更多的可能性 关于互联网大厂的笔试面试,都是需要细心准备的 (1)自己的科研经历,科研内容,学习的相关领域知识,要熟悉熟透了 (2)自己的实习经历
任意一点X0到超平面S的距离以及拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
转自: http://blog.csdn.net/xinzaichenmo/article/details/70161728 http://blog.csdn.net/xianlingmao/article/details/7919597 在求取有约束条件的优化问题时,拉格朗日乘子法(Lagrange Multiplier) 和KKT条
拉格朗日乘子法与KKT条件核心原理(小白都能看懂)
文章目录 问题背景等式约束条件下的最优化不等式约束条件下的最优化问题多条件约束下的最优化问题KKT条件 问题背景 假设有一座山,山上有一条路。我们只能走在这条路上,其他的地方无法到达。在此基础上,我想知道我始终在路上的情况下,可能达到的最高点及其高度。 拉格朗日乘子法和KKT条件解决的正是这么个问题。我们想知道在某个约束条件(山间小路)的限制下,所能达到的最值点(最大高度)。是
约束下的最优求解:拉格朗日乘数法和KKT条件
机器学习面对各种各样的求解极值或者最值问题 ,现在对常见的求解极值或者最值问题思路做一下理论上的梳理。 最值问题 简单了解最值问题 求最值是非常常见的问题,比如如何选择交通路线,最快地到达某地;如何用手头的钱买到分量最重的水果等等。 我们可以把需求定义为一个目标函数: f(x) f(x) 最值问题也就可以表示为 min[f(x)] min [ f(x) ] 对于一个
深入理解拉格朗日乘子法和KKT条件的原理及运用
深入理解拉格朗日乘子法和KKT条件的原理及运用 一、凸函数二、常见的三类最优化问题三、拉格朗日乘子法解决带等式约束的最优化问题(一)用实例理解拉格朗日乘子法的背后意义(二)、拉格朗日乘子法求解带等式约束的最优化问题 四、引入KKT条件求带不等式约束条件的最优化(一)实例理解带不等式约束条件的最优化(二)满足KKT条件下的利用拉格朗日函数求带不等式约束的最优化问题(三)原最优化问题转对偶问题
拉格朗日松弛法、KKT条件与线性规划的对偶
拉格朗日松弛 深度解析拉格朗日乘子法,让你成为高手 对于等式约束,实际上是存在一条等值线,最优解必须存在在这条解上。 其目的是判断约束 g ( x ) g(x) g(x)的梯度方向是否和等值线的梯度方向共线。 即: [ x 1 , x 2 , x 3 ] T = λ [ y 1 , y 2 , y 3 ] [x_1,x_2,x_3]^T=\lambda[y_1,y_2,y_3]