本文主要是介绍手推支持向量机03-硬间隔SVM-模型求解(对偶问题之KKT条件),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.写在前面
2.KTT条件
3.求最终的w*,b*和最终的决策函数
1.写在前面
上面我们讲到了怎么对硬间隔SVM进行求解,我们我们先把带约束问题,转化为无约束问题,通过强对偶关系将minmax转为maxmin,对w,b求min,最终我们求出来最小值,然后关于λ求最大值。

我们最后圈出来的地方,可以变成min,只需要在后面加上符号。因为习惯上用最小化表达,并且这个位置把约束也补全了。

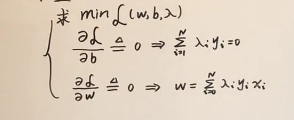
这篇博客我们重点看一下上面的优化函数怎么求解,这个函数是一个关于λ的min问题函数。
2.KTT条件
Karush-Kuhn-Tucker (KKT)条件是非线性规划(nonlinear programming)最佳解的必要条件。KKT条件将Lagrange乘数法(Lagrange multipliers)所处理涉及等式的约束优化问题推广至不等式。在实际应用上,KKT条件(方程组)一般不存在代数解,许多优化算法可供数值计算选用。原问题,对偶问题具有强对偶关系的充要条件就是他们满足KTT条件。maxmin和minmax默认条件下,一定是满足弱对偶关系,然后因为它是一个凸二次规划问题,约束是线性的,目标函数是二次的,所以满足强对偶关系(此处需要证明)。
我们这个问题整个的KTT条件是:

3.求最终的w*,b*和最终的决策函数
我们得到上面的条件,就可以求出最终的w*,b*和最终的决策函数超平面。注:第二个重要条件是互补松弛条件。

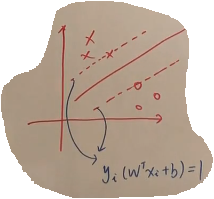
超平面就是f(x)去掉sign函数即可。w*实际上可以看做关于数据Xi的线性组合,λi大部分时候都是等于0的,只有对KKT第四个条件等于0的时候有意义(有限的点,有限的支持向量,下面两条虚线上点就叫support vector支持向量)。
这篇关于手推支持向量机03-硬间隔SVM-模型求解(对偶问题之KKT条件)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







