svm专题
SVM编程实现python
深入解析python版SVM源码系列--简化版SMO算法 SVM使用SMO算法来解决其中涉及到的二次规划问题。一个简单版本的SMO算法的实现如下: ''' 随机选择随机数,不等于J '''def selectJrand(i,m):j=i #we want to select any J not equal to iwhile (j==i):j = int(random
机器学习项目——基于机器学习(决策树 随机森林 朴素贝叶斯 SVM KNN XGBoost)的帕金森脑电特征识别研究(代码/报告材料)
完整的论文代码见文章末尾 以下为核心内容和部分结果 问题背景 帕金森病(Parkinson’s Disease, PD)是一种常见的神经退行性疾病,其主要特征是中枢神经系统的多巴胺能神经元逐渐丧失,导致患者出现运动障碍、震颤、僵硬等症状。然而,除运动症状外,帕金森病患者还常常伴有一系列非运动症状,其中睡眠障碍是最为显著的非运动症状之一。 脑电图(Electroencephalogram, E
《西瓜书》第六章 SVM支持向量机 笔记
文章目录 6.1 间隔与支持向量6.1.1 超平面6.1.2 支持向量6.1.3 间隔6.1.4 最大间隔 6.2 对偶问题6.2.1 凸二次规划6.2.2 对偶问题6.2.3 支持向量机的一个重要性质 6.3 核函数6.3.1 支持向量展开式6.3.2 核函数定理6.3.3 常用的核函数6.3.4 核函数特点 6.4 软间隔与正则化6.4.1 硬间隔6.4.2 软间隔6.4.3 替代损失6
深度学习速通系列:贝叶思和SVM
贝叶斯方法和支持向量机(SVM)是两种在机器学习领域中广泛使用的算法,它们各自有着独特的优势和应用场景。下面详细介绍这两种算法及其实际应用和使用案例。 贝叶斯方法 概述: 贝叶斯方法基于贝叶斯定理,通过结合先验知识和观测数据来更新对假设的信念。这种方法在处理不确定性和概率推断方面非常有效。 核心原理: 贝叶斯定理: P ( A ∣ B ) = ( P ( B ∣ A ) ⋅ P ( A
自然语言处理系列五十》文本分类算法》SVM支持向量机算法原理
注:此文章内容均节选自充电了么创始人,CEO兼CTO陈敬雷老师的新书《自然语言处理原理与实战》(人工智能科学与技术丛书)【陈敬雷编著】【清华大学出版社】 文章目录 自然语言处理系列五十SVM支持向量机》算法原理SVM支持向量机》代码实战 总结 自然语言处理系列五十 SVM支持向量机》算法原理 SVM支持向量机在文本分类的应用场景中,相比其他机器学习算法有更好的效果。下面介绍其
算法——支持向量机(support vector machines,SVM)
简介:个人学习分享,如有错误,欢迎批评指正 支持向量机(Support Vector Machine, SVM)是一种监督学习算法,广泛用于分类任务,也可以用于回归和异常检测等问题。SVM的核心思想是通过在特征空间中找到一个最优的分隔超平面,将不同类别的数据点分开,使得各类别之间的间隔最大化。 一、SVM的基本概念 1. 超平面 在二维空间中,超平面就是一条直线,而在高维空间中,超平面
Spark Mllib之线性SVM和逻辑回归
微信公众号:数据挖掘与分析学习 1.Mathematical formulation 许多标准机器学习方法可以被公式化为凸优化问题,即找到取决于具有d个条目的变量向量w(在代码中称为权重)的凸函数f的最小化的任务。形式上,我们可以将其写为优化问题,其中目标函数形式如下: 这里向量xi∈Rd是训练数据的样本,对于1≤i≤n,yi∈R是它们对应的我们想要预测的标签。如果L(w; x,y)可以
基于SVM的手势识别,SVM工具箱详解,SVM工具箱使用注意事项
目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 Libsvm工具箱详解 简介 参数说明 易错及常见问题 SVM应用实例,基于支持向量机SVM的手势识别 代码 结果分析 展望 摘要 基于支持向量机SVM的手势识别,SVM原理,SVM工具箱详解,SVM常见改进方法 支持向量机SVM的详细原理 SVM的定义 支持向量机(support vector machines, SVM)
深度学习速通系列:贝叶思SVM
贝叶斯(Bayesian)方法和支持向量机(SVM,Support Vector Machine)是两种不同的机器学习算法,它们在解决分类和回归问题时有着不同的原理和应用场景 贝叶斯方法: 贝叶斯方法基于贝叶斯定理,这是一种利用已知信息(先验概率)来预测未知事件(后验概率)的概率方法。它通常用于分类问题,特别是当数据集较小或存在类别不平衡时。贝叶斯方法可以处理不确定性,并且可以通过增加新的数据
C++开发人脸性别识别教程(6)——通过SVM实现性别识别
上一篇教程中我们介绍了如何使用OpenCv封装的FaceRecognizer类实现简单的人脸性别识别,这里我们为大家提供另外一种基本的性别识别手段——支持向量机(SVM)。 支持向量机在解决二分类问题方面有着强大的威力(当然也可以解决多分类问题),性别识别是典型的二分类模式识别问题,因此很适合用SVM进行处理,同时OpenCv又对SVM进行了很好的封装,调用非常方便,因此我们在这个性
《机器学习》 SVM支持向量机 推导、参数解析、可视化实现
目录 一、SVM支持向量机 1、什么是SVM 例如: 2、SVM的主要特点是: 二、SVM方程 1、超平面方程 2、标签问题 3、决策函数: 符号函数: 整合: 4、距离问题 1)点到直线距离 2)点到平面距离 3)点到超平面距离 简写: 改进:加上正确性 分类正确时: 两个衡量指标: 5、如何找到最优超平面 1)找到距离超平面最近点 2)最大化这个距离
sheng的学习笔记-AI-半监督SVM
AI目录:sheng的学习笔记-AI目录-CSDN博客 svm: sheng的学习笔记-AI-支持向量机(SVM)-CSDN博客 半监督学习: sheng的学习笔记-AI-半监督学习-CSDN博客 什么是半监督svm 半监督支持向量机(Semi-Supervised Support Vector Machine,简称S3VM)是支持向量机在半监督学习上的推广。 在不考虑未标记样本时,
sklearn光速入门实践[1]——实现一个简单的SVM分类器
python的sklearn库封装了许多常用的机器学习算法,而且入门简单,调用方便。下面我们用sklearn库和简单的几个点作为数据集,来实现一个简单的SVM分类器。 首先,准备好数据。我们把(2,0),(0,2),(0,0)这三个点当作类别1;(3,0),(0,3),(3,3)这三个点当作类别2,训练好SVM分类器之后,我们预测(-1,-1),(4,4)这两个点所属的类别。示意图如下: 1
吴恩达机器学习课后作业-06支持向量机(SVM)
SVM 线性可分SVM题目绘制决策边界改变C,观察决策边界代码 线性不可分SVM核函数代码 寻找最优C、gamma垃圾邮件过滤 线性可分SVM 题目 数据分布 绘制决策边界 import numpy as npimport matplotlib.pyplot as pltimport scipy.io as siofrom scipy.optimize i
小琳 AI 课堂:SVM支持向量机
哈喽,亲爱的小伙伴们!这里是小琳 AI 课堂😜 今天咱们要好好聊聊超级厉害的支持向量机(Support Vector Machine,SVM)👏 它在机器学习领域那可是一颗耀眼的明星✨ 🎯说到技术细节,SVM 属于有监督的学习算法,既能搞定分类问题,又能处理回归问题,简直牛到不行😎 它的核心呢,就是在特征空间里拼命寻找一个超级厉害的超平面,把不同类别的样本分得清清楚楚👀 要是遇到线性
基于python的自适应svm电影评价倾向性分析设计与实现
博主介绍: 大家好,本人精通Java、Python、C#、C、C++编程语言,同时也熟练掌握微信小程序、Php和Android等技术,能够为大家提供全方位的技术支持和交流。 我有丰富的成品Java、Python、C#毕设项目经验,能够为学生提供各类个性化的开题框架和实际运作方案。 我擅长在JavaWeb、SSH、SSM、SpringBoot+VUE、VUE+FastApi、Python+Djan
SVM(Support Vector Machine)分类器详解
1. 拉格朗日乘子(Lagrange multiplier)法求解条件极值 1.1 拉格朗日乘子的简单描述 简单的条件极值问题可以描述为:求函数 z = f ( x , y ) z=f(x,y) z=f(x,y)的最大值,且 x , y x,y x,y满足约束条件 φ ( x , y ) = M \varphi (x,y)=M φ(x,y)=M( M M M已知)。 拉格朗日乘子的求解步骤为:





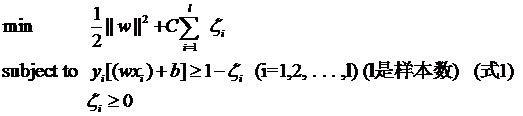
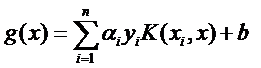

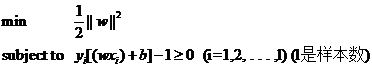
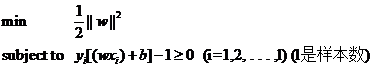









![sklearn光速入门实践[1]——实现一个简单的SVM分类器](https://i-blog.csdnimg.cn/blog_migrate/37b1cd9f70b70b7a88429c60af5e31b8.png)

