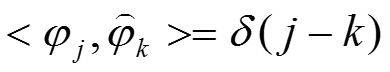对偶专题

【调度算法】对偶问题和影子价格

一、场景引入先看一个示例：场景：农场主和市场假设你是一个农场主，种植了玉米和小麦。你有一块地，同时有一定量的肥料和水资源。你需要决定如何分配这些资源来种植玉米和小麦，以最大化你的收益。原问题你的原问题是：如何分配你的土地、肥料和水，使得你种植的玉米和小麦的总收益最大化？在这个问题中，你会考虑：每种作物需要多少土地？每种作物需要多少肥料和水？每种作物在市场上能卖多少钱？

通俗范畴论11 对偶范畴与余积

对偶范畴与余积对偶的通俗意义对偶，我们并不陌生，例如唐朝杜甫的《绝句》：两个黄鹂鸣翠柳，一行白鹭上青天。窗含西岭千秋雪，门泊东吴万里船。 — 唐杜甫上面这首诗，是唐朝杜甫的《绝句》，我们可以发现，“两个”对应“一行”，“黄鹂”对应“白鹭”…，就说该诗中的上句，总是要求其下句的对应，这就是对偶。在范畴论中，对偶

CVPR2020丨DRN：用于单图像超分辨率的对偶回归网络

点击上方“AI公园”，选择“星标★”公众号重磅干货，第一时间送达论文：https://arxiv.org/pdf/2003.07018.pdf代码：https://github.com/guoyongcs/DRN 目前超分辨率算法存在两个明显的问题：从 LR 图像到 HR 图像通常是一个高度病态的反问题，存在无数可能的HR 图像通过降采样得到同一张 LR 图像。解空间过大，从而很难去找

SVM(二）从拉格朗日对偶问题到SVM

2.1 拉格朗日对偶（Lagrange duality）先抛开上面的二次规划问题，先来看看存在等式约束的极值问题求法，比如下面的最优化问题：目标函数是f(w)，下面是等式约束。通常解法是引入拉格朗日算子，这里使用来表示算子，得到拉格朗日公式为 L是等式约束的个数。然后分别对w和求偏导，使得偏导数等

机器学习：深入解析SVM的核心概念（问题与解答篇）【二、对偶问题】

对偶问题 ==**问题一：什么叫做凸二次优化问题？而且为什么符合凸二次优化问题？**==为什么约束条件也是凸的半空间（Half-Space）凸集（Convex Set）半空间是凸集的例子SVM 约束定义的半空间总结 ==**问题二：为什么使用拉格朗日乘子法？原理是什么？**==为什么使用拉格朗日乘子法拉格朗日乘子法的数学原理结合简单例子理解定义问题构建拉格朗日函数对拉格朗日函数求偏导数解方程

[机器学习必知必会]拉格朗日法及其对偶问题

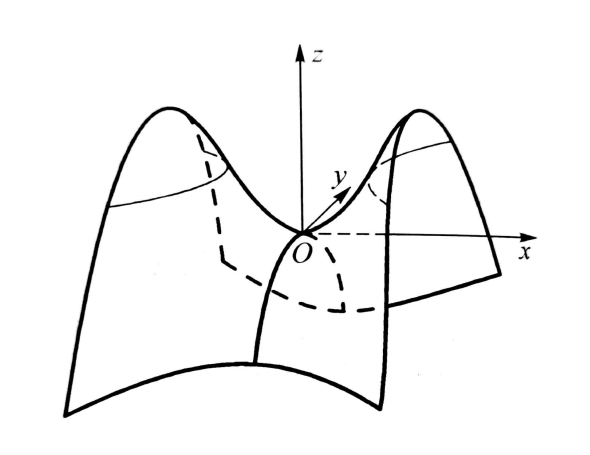
了解一些简单的数学概念首先看一个二元函数（再复杂一点的函数就很难直观地呈现出来）的三维图像和对应的等高线，其中函数表达式为 z = x 2 + y 2 z=x^2+y^2 z=x2+y2：从导数到偏导数对于一个一元函数而言，导数的定义想必大家都很清楚，具体的表达式为： f ′ ( x ) = lim ⁡ △ x → 0 f ( x + △ x ) − f ( x ) △ x =

感知机对偶形式完美解释

离散数学——（3）联结词及对应的真值指派，最小全功能联结词集，对偶式，范式，范式存在定理，小项

目录 1.联结词及对应的真值指派 2.最小全功能联结词集 3.对偶式 4.范式 1.析取范式 5.范式存在定理 6.小项 1.联结词及对应的真值指派 2.最小全功能联结词集 3.对偶式 4.范式 1.析取范式 5.范式存在定理 6.小项

手推支持向量机03-硬间隔SVM-模型求解（对偶问题之KKT条件）

目录 1.写在前面 2.KTT条件 3.求最终的w*，b*和最终的决策函数 1.写在前面上面我们讲到了怎么对硬间隔SVM进行求解，我们我们先把带约束问题，转化为无约束问题，通过强对偶关系将minmax转为maxmin，对w,b求min，最终我们求出来最小值，然后关于λ求最大值。我们最后圈出来的地方，可以变成min，只需要在后面加上符号。因为习

凸优化学习-（十九）深入分析对偶问题

凸优化学习学习笔记一、原问题最优值 p ∗ \text p^* p∗与与对偶问题最优值 d ∗ \text d^* d∗分析 1、背景知识对于一个普通优化问题： min ⁡ f 0 ( x ) ( P ) s.t. f i ( x ) ≤ 0 i = 1 ⋯ m h i ( x ) = 0 i = 1 ⋯ p \begin{aligned} \min&& f_0(x)&\\ (\t

机器学习----SVM（2）从原始问题到对偶问题的转换

SVM的水真是太深了，只能一点一点的解决了，今天这篇博客简单讲解SVM的目标函数从原始问题到对偶问题的转换。在这里再给大家一个大牛的博客链接：http://blog.pluskid.org/?p=685 1、转化对偶问题上篇博客中我们得到的目标函数：（1）我们在优化时喜欢求最小值，将上式转化正等价的求最小值如下：（2）对于（2）式，这是一个凸二次规划问题，我们可以

SVM使用对偶、核函数、软间隔的动机

使用对偶问题动机 SVM可以通过QP即二次规划求解，通过QP求解时问题的求解复杂度是与是与输入特征的维度相关的，在对原来的X进行使用核函数做升维度后，此时的维度会非常的大。例如使用二次多项式核函数时，映射后的维度为原始维度的平方倍数量级，如果使用高斯核函数则映射后的维度为无穷维。所以此时再使用QP解原始的SVM最小化问题效率会非常低下，这就引出了通过解SVM的对偶问题来解原始最优化问题，而原始S

从L1,L2正则，到KKT条件下的拉格朗日乘法到拉格朗日对偶问题

转：相对清晰的一篇博客从loss的l1,l2正则，追溯到模型复杂度衡量，追溯到不等式极值问题，以下两篇文章，可以进一步深入了解背后的数学原理 L1、L2正则化和过拟合 [从KKT条件下的拉格朗日乘法到拉格朗日对偶问题]

【数学】拉格朗日对偶，从0到完全理解

https://blog.csdn.net/frostime/article/details/90291392

svm的对偶，kkt，拉格朗日乘子法

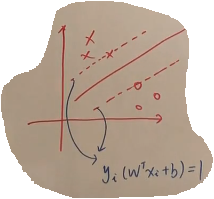
原文链接：https://blog.csdn.net/bit_666/article/details/79865225 1.SVM基础模型给定训练集D={(x1,y1),(x2,y2)...(xn,yn)},yi∈{-1,1}，例如下面图中的点，蓝线左上方的6个点对应1类，右下方的6个点对应-1类，基于数据分类的思想，如果我们想把两类数据分开，显然蓝线不是唯一的选择，我们有无数条直线可以选择

对偶问题的基本性质

写于：2024年1月3日晚修改于：原规划与对偶规划原规划对偶规划 max ⁡ z = C T X s.t. { A X ≤ b , 其中 X ( m ∗ 1 ) X ≥ 0 \begin{aligned} & \max \mathrm{z}=\mathbf{C}^T \mathbf{X} \\ & \text { s.t. }\left\{\begin{array}{l}\ma

BZOJ 1001 狼抓兔子（最大流-对偶图最短路）

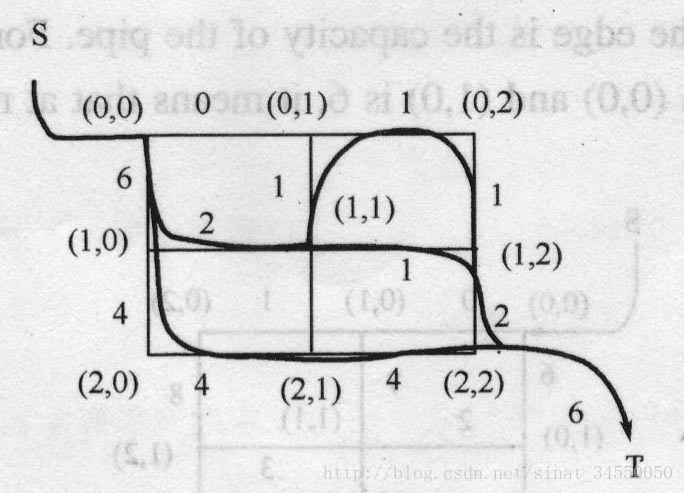
题目链接：http://61.187.179.132/JudgeOnline/problem.php?id=1001 题意：如下图。每条边的权值为容量。源点在左上角，汇点在右下角。求s到t的最大流。思路：（1）平面图：按照我的理解，平面图就是所有的边只在顶点处相交的图；（2）对偶图：我们将一个图其中的面看做点，一条边所分隔开的两个面之间连一条权值为这条边的权值的边。那么

拉格朗日对偶问题详解

参考: 1, http://www.cnblogs.com/90zeng/p/Lagrange_duality.html 2, https://blog.csdn.net/u011327333/article/details/51222605 3, https://en.wikipedia.org/wiki/Duality_(optimization)

Cogs 750. 栅格网络(对偶图)

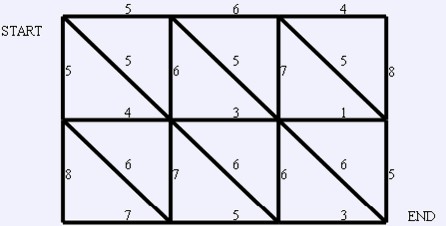
栅格网络流 ★★☆ 输入文件：flowa.in 输出文件：flowa.out 简单对比时间限制：1 s 内存限制：128 MB 【问题描述】 Bob 觉得一般图的最大流问题太难了，他不知道如何解决，于是他想尝试一个简单点的：栅格网络中的最大流问题，这个虽说简单了一点，但对 Bob 来说依旧太难，现在他有个麻烦需要你帮忙：给你一个 N*M 的栅格（如下所示），栅格中的边表示可以流水的管道

约束极值问题之拉格朗日乘子法、KKT条件与对偶理论

文章目录 1 等式约束极值问题1.1 拉格朗日乘子法（必要条件） 2 不等式约束极值问题2.1 约束作用2.2 不等式约束的几何解释2.3 下降方向2.4 可行方向2.5 Fritz John条件（最优解必要条件）2.6 Kuhn-Tucker条件（最优解必要条件 - 约束规格）2.7 最优解必要条件 3 对偶问题3.1 原始问题的等价问题3.2 原始问题的对偶问题3.3 原始问题与对偶问题

对偶问题笔记（1）

目录 1 从 Lagrange 函数引入对偶问题2. 强对偶性与 KKT 条件3. 对偶性的鞍点特征 1 从 Lagrange 函数引入对偶问题考虑如下优化问题 { min ⁡ f 0 ( x ) s . t f i ( x ) ≤ 0 , i = 1 , ⋯ , p , h j ( x ) = 0 , j = 1 , ⋯ , q , x ∈ Ω , \begin{align}

原始问题与对偶问题

原始问题与对偶问题（转）每一个线性规划问题，我们称之为原始问题，都有一个与之对应的线性规划问题我们称之为对偶问题。原始问题与对偶问题的解是对应的，得出一个问题的解，另一个问题的解也就得到了。并且原始问题与对偶问题在形式上存在很简单的对应关系： * 目标函数对原始问题是极大化,对对偶问题则是极小化 * 原始问题目标函数中的收益系数（优化函数中变量前面的系数）是对偶问题约束不等式中的右端常数,

信号分解：标架、对偶标架、紧标架

1.前言信号分解或信号变换的基本思路是将信号x(t)和一组函数（或向量）做內积，从而得到一组分解系数a n 。分解（或变换）的目的是研究原始信号中有哪些有哟用的信息，并讨论如何抽取这些有用的信息。我能能够理解，正交基具有很多优点（信息不冗余，对偶基是本身），实际应用中也是最广泛的，可惜的是，在实际工作中，发现并得到一组好的正交基往往是不容易的。正式正交基，或者更广泛地说，分解

约束优化之Lagrange乘子法KKT条件对偶问题最容易理解解读

1.无约束优化的常用方法在讲带约束优化方法之前，我们先简单回顾一下常用的无约束优化方法。 1.梯度下降法 2.牛顿法/拟牛顿法 3.共轭梯度法 … 上面梯度系列的无约束条件下的最优化，基本解法是根据极值的必要条件一阶导数为0，通过泰勒展开等形式，构造不同数列不断逼近最优解。 2.带约束的优化实际情况中，不带约束的场景比较少见，大部分都为带约束的优化问题。看一个大家都用的图：上图中，

$优化问题的拉格朗日Lagrange对偶法原理$

优化问题的拉格朗日Lagrange对偶法原理

首先我们定义一般形式的求解x的优化问题：表示优化的目标函数，上述为最小优化，实际上最大优化可以改写为的形式表示第i个不等式约束表示等式约束 1. Lagrange对偶问题上述优化问题的拉格朗日Lagrange对偶法求解，是将上述带约束的目标优化问题改写为如下无约束的Lagrange函数式子。上述Lagrange函数式子存在如下对偶函数，其是Lagrange函数关于取最小值，即

BZOJ 2007 浅谈对偶图优化网络流

世界真的很大网络流的东西果然水还是很深不光是建边非常玄学，这个优化还是有条件的有时题目会故意坑你，不要轻易相信题面给出的提示看题先: description YT市是一个规划良好的城市，城市被东西向和南北向的主干道划分为n×n个区域。简单起见，可以将YT市看作一个正方形，每一个区域也可看作一个正方形。从而，YT城市中包括(n+1)×(n+1)个交叉路口和2n×(n+1)条