本文主要是介绍Depth-First深度优先、Breadth-First广度优先、Iterative Deepening迭代深入、Uniform Cost代价一致搜索算法的规则及基于n叉树的时间复杂度空间复杂度比较,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Depth-First深度优先、Breadth-First广度优先、Iterative Deepening迭代深入、Uniform Cost代价一致搜索算法
分为两部分介绍:
- 四种算法的遍历规则
- 基于n叉树的时间复杂度与空间复杂度比较
四种算法的遍历规则
使用下图案例来比较四种算法的遍历规则:

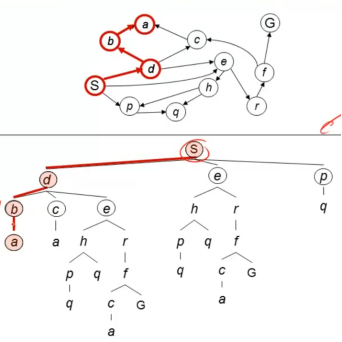
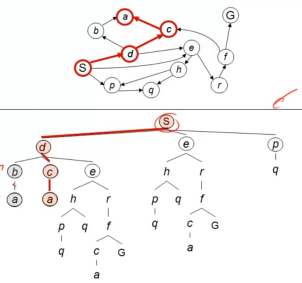
1. Depth-First Search 深度优先算法
策略:优先遍历最深节点
实现:存贮邻接点使用LIFO stack后进先出的栈
 |  |
|---|---|
 |  |
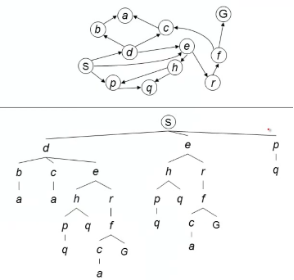
2. Breadth-First Search 广度优先算法
策略:优先遍历最浅的一层节点,从上自下,一层层遍历
实现:存贮邻接点使用FIFO queue先入先出数列
 |  |
|---|
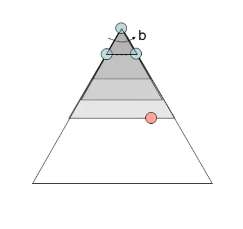
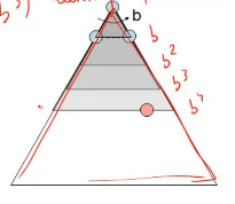
3. Iterative Deepening迭代加深算法
限制一个深度d1用深度优先算法遍历,如果没有目标
限制一个深度d2用深度优先算法遍历,如果没有目标
限制一个深度d3…
 |  |
|---|
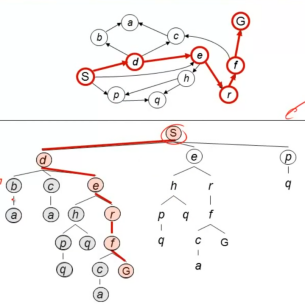
4. Uniform Cost Search代价一致算法
策略:确定邻接节点的集合,从中选取,优先添加花费最小的节点(注意图三优先选取邻接节点中最小的e,即使目标节点已经邻接表中,图四不同颜色表示邻接节点集合范围)
实现:存贮邻接点使用Priority queue优先级数列(优先级为:累计成本)
 |  |
|---|---|
 |  |
基于n叉树的时间复杂度与空间复杂度比较
用下图b叉树来比较四种算法的时间复杂度与空间复杂度(b是子节点个数,m是b叉树的层数,总的节点数: 1 + b + b 2 1+b+b^2 1+b+b2+… + b m +b^m +bm = O ( b m ) =O(b^m) =O(bm))

1. Depth-First Search 深度优先算法
时间复杂度:O( b m b^m bm),考虑最坏情况目标在树的右下角,所以需要遍历所有节点

空间复杂度:O(bm),空间复杂度也就是存贮邻接点的大小,LIFO stack后进先出的栈的容量,考虑最坏情况如图遍历到m层每一层需要存贮相邻的b个节点,故节点个数为bm

2. Breadth-First Search 广度优先算法
时间复杂度: O ( b s ) O(b^s) O(bs),引入新变量s,即达到目标的最浅层数,故时间复杂度为遍历目标节点前的所有节点 b s b^s bs
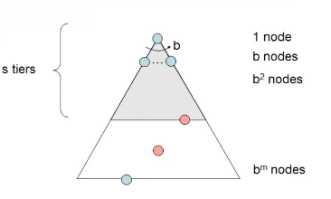
空间复杂度: O ( b s ) O(b^s) O(bs),邻接节点即每一层,考虑最坏情况在s层时,节点个数为 b s b^s bs
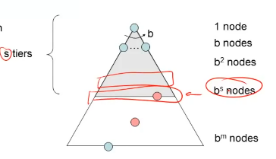
3. Iterative Deepening迭代加深算法
时间复杂度:O ( b s ) (b^s) (bs),同广度优先算法
空间复杂度: O ( b ∗ s ) O(b*s) O(b∗s),同深度优先算法,但最差情况由第m层变为找到目标的s层
同时汲取了深度优先算法的空间复杂度优势,及广度优先算法的时间shallow-solution较浅情况优势
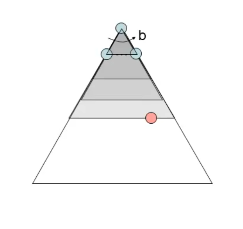
4. Uniform Cost Search代价一致算法
时间复杂度: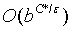 ,C是代价, C ∗ C* C∗是代价的最优值, ϵ \epsilon ϵ指每一步代价至少为,有效深度(effective depth)大约为层C*/ ϵ \epsilon ϵ
,C是代价, C ∗ C* C∗是代价的最优值, ϵ \epsilon ϵ指每一步代价至少为,有效深度(effective depth)大约为层C*/ ϵ \epsilon ϵ
空间复杂度: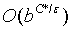
 | 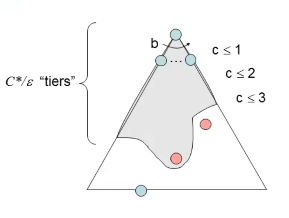 |
|---|
这篇关于Depth-First深度优先、Breadth-First广度优先、Iterative Deepening迭代深入、Uniform Cost代价一致搜索算法的规则及基于n叉树的时间复杂度空间复杂度比较的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






