322专题

代码随想录：322. 零钱兑换

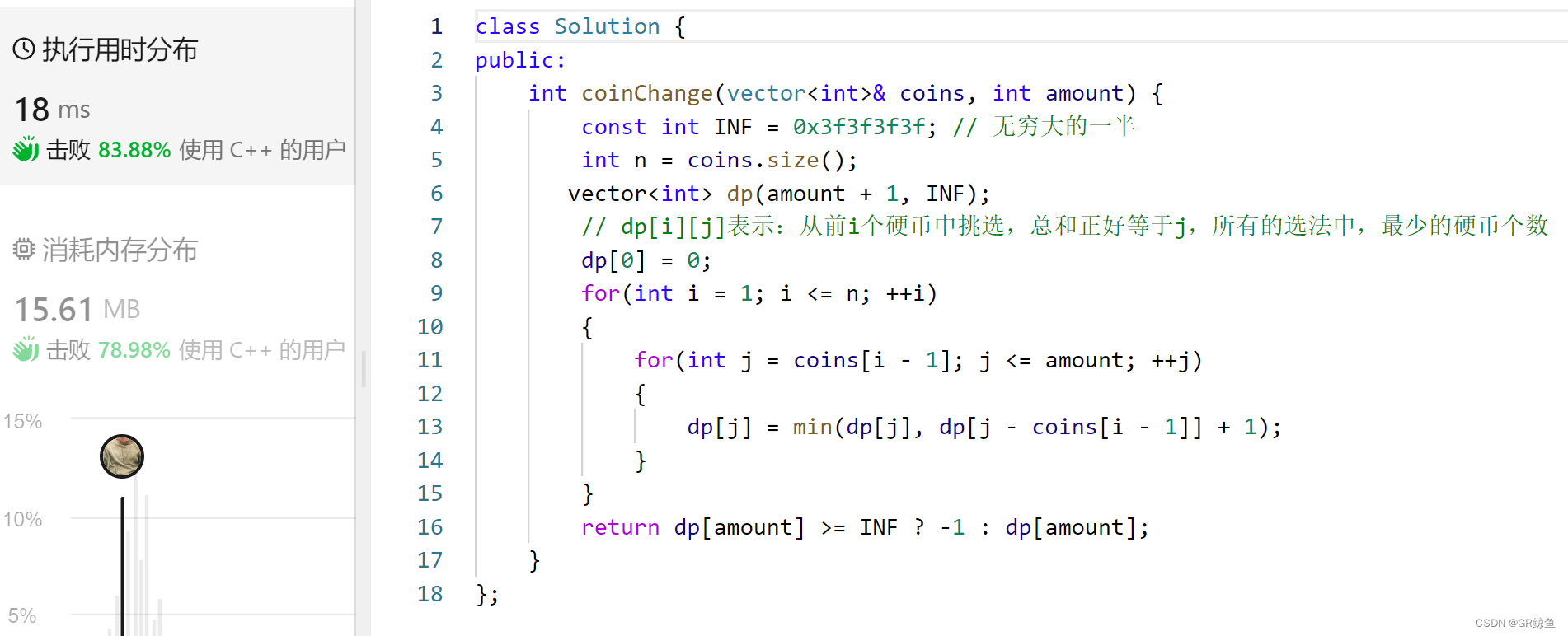
322. 零钱兑换 class Solution {public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(10005,INT_MAX);//由于后面要取最小值，所以初始大一些dp[0]=0;//总金额为0个数一定为0for(int i=0;i<coins.size();i++){for(int j=coins

代码随想录训练营 Day38打卡动态规划 part06 322. 零钱兑换 279. 完全平方数 139. 单词拆分

代码随想录训练营 Day38打卡动态规划 part06 一、力扣322. 零钱兑换给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。示例：输入：coins = [1, 2, 5], amount = 1

【代码随想录训练营第42期 Day38打卡 - 动态规划Part6 - LeetCode 322. 零钱兑换 279.完全平方数 139.单词拆分

目录一、做题心得二、题目与题解题目一：322. 零钱兑换题目链接题解：动态规划--完全背包题目二： 279.完全平方数题目链接题解：动态规划--完全背包题目三：139.单词拆分题目链接题解：动态规划--完全背包三、小结一、做题心得今天来到了代码随想录动态规划章节的Part6，依旧是完全背包问题的应用。相对于前边直接套用模板，今天

代码随想录算法训练营Day44|322.零钱兑换、279.完全平方数、139.单词拆分

零钱兑换 322. 零钱兑换 - 力扣（LeetCode）本题是完全背包问题 dp数组表示组成amount金额所需的最少硬币个数。考虑dp数组的推导公式，由于是计算最少硬币的个数，所以需要考虑dp[i-coins[j]+1和dp[i]的较小值。所以dp[i] = min(dp[i-coins[j]]+1,dp[i])，其中i为遍历过程中的amout值，coins[j]为硬币的面值。

【代码随想录算法训练Day44】LeetCode 322.零钱兑换、LeetCode 279.完全平方数、LeetCode139.单词拆分

Day44 动态规划第六天 LeetCode 322.零钱兑换 dp数组的含义：装满容量为j的背包需要的最少物品数为dp[j] 递推公式：dp[j]=min(dp[j-coins[i]]+1,dp[j]) 初始化：dp[0]=0,dp[j]=INT_MAX 遍历顺序：个数问题与遍历顺序无关，都可以 class Solution {public:int coinChange(vector<i

代码随想录算法训练营第44天（py）| 动态规划 | 322. 零钱兑换、279.完全平方数、139.单词拆分

322. 零钱兑换力扣链接给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。思路每种硬币数量无限，是多重背包问题。确定dp含义凑到总金额为i的最少硬币个数为dp[i]确定递推公式凑足总额为j -

【代码随想录】【算法训练营】【第44天】 [322]零钱兑换 [279]完全平方数 [139]单词拆分

前言思路及算法思维，指路代码随想录。题目来自 LeetCode。 day 44，周四，坚持不住了~ 题目详情 [322] 零钱兑换题目描述 322 零钱兑换解题思路前提：思路：重点：代码实现 C语言 [279] 完全平方数题目描述 279 完全平方数解题思路前提：思路：重点：代码实现 C语言 [139] 单词拆分

代码随想录算法训练营第四十三天| 377. 组合总和 Ⅳ、57. 爬楼梯（第八期模拟笔试）、322. 零钱兑换、279. 完全平方数

[LeetCode] 377. 组合总和 Ⅳ[LeetCode] 377. 组合总和 Ⅳ 文章解释 [LeetCode] 377. 组合总和 Ⅳ 视频解释题目：给你一个由不同整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。题目数据保证答案符合 32 位整数范围。示例 1：输入：nu

算法刷题 322. 零钱兑换

322. 零钱兑换给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。示例 1：输入：coins = [1, 2, 5], amount = 11 输出：3 解释：11 = 5 + 5 + 1 示例

【代码随想录】【算法训练营】【第30天】 [322]重新安排行程 [51]N皇后 [37]解数独

前言思路及算法思维，指路代码随想录。题目来自 LeetCode。 day 30，周四，好难，会不了一点~ 题目详情 [322] 重新安排行程题目描述 322 重新安排行程解题思路前提：…… 思路：回溯。重点：……。代码实现 C语言回溯 + 链表自实现超出时间限制！！ /*** Note: The returned array must be mall

代码随想录算法训练营第四十八天| km57. 爬楼梯、322. 零钱兑换、279.完全平方数

代码随想录算法训练营第四十八天 km57. 爬楼梯题目链接：km57. 爬楼梯确定dp数组以及下标的含义：j为背包的最大容量，dp[j]当容量为j有几种组合方式确定递推公式：dp[j]=dp[j]+dp[j-i]，不放当前数字组成目标值的种类+必须放当前数字组成目标值的种类（为了保证一定放这个值，就要把需要的容量腾出来）dp数组如何初始化：容量为0，有一种放法，dp[0] = 1;确

随想录Day48 57.爬楼梯进阶 322.零钱兑换 279.完全平方数

随想录Day48 57.爬楼梯进阶 322.零钱兑换 279.完全平方数 57.爬楼梯进阶题目链接假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢？注意：给定 n 是一个正整数。完全背包 # include <iostream># include <vector>using namespa

代码随想录｜Day42｜动态规划 part07｜● 70. 爬楼梯（进阶）● 322. 零钱兑换 ● 279.完全平方数

70. 爬楼梯（进阶） 322. 零钱兑换 class Solution: def climbStairs(self, n: int) -> int: if n <= 1: return n dp = [0] * (n + 1) dp[0] = 0 dp[1] = 1

第四十五天 | 322.零钱兑换

题目：322.零钱兑换尝试解答： 1.确定dp[j]含义：装满容量为j的背包所需要放的硬币个数为dp[j]; 2.动态转移方程：dp[j] = dp[j - coins[i]] + 1; 3.遍历顺序：本题应该为组合类题目，不考虑装入的顺序，只在乎硬币个数所以先物品后背包，背包容量从小到大。（错） 4.初始化：dp[0] = 1,其余均初始换为0 5.打印dp

力扣HOT100 - 322. 零钱兑换

解题思路：动态规划 class Solution {public int coinChange(int[] coins, int amount) {int[] dp = new int[amount + 1];Arrays.fill(dp, amount + 1);dp[0] = 0;for (int i = 1; i <= amount; i++) {for (int j = 0;

代码随想录算法训练营第四十五天|70. 爬楼梯（进阶版），322. 零钱兑换，279.完全平方数

目录 70. 爬楼梯（进阶版）思路代码 322. 零钱兑换思路代码 279.完全平方数思路代码 70. 爬楼梯（进阶版）题目链接：57. 爬楼梯（第八期模拟笔试）文档讲解：代码随想录思路完全背包问题，物品为每次可以爬的台阶数，背包容量为所需要爬的台阶数，求装满该背包有多少种方法，而且需要考虑顺序。代码 #include <iostream>#inclu

[算法导论] 322.零钱兑换(dp)

目录 0. 题目 1. 动态规划代码 1. 用币种更新 o(amount

代码随想录第45天 | 70. 爬楼梯（进阶）、 322. 零钱兑换、 279.完全平方数

一、前言：参考文献：代码随想录今天的主题是完全背包，要牢记完全背包和01背包的区别；一个是物品无限次使用，另一个是物品只能使用一次；二、爬楼梯（进阶） 1、思路：这一个题目首先要弄清楚谁是背包，谁是物品，我一开始就弄反了，结果就出错了，还有递推公式是怎么来的。继续动态规划五部曲：前提n为楼梯阶数，m为爬楼梯的能力，一次最多怕几阶层（1）dp数组： vector<i

代码随想录算法训练营第四十五天| 70. 爬楼梯（进阶），322. 零钱兑换，279.完全平方数

题目与题解 70. 爬楼梯（进阶）题目链接：70. 爬楼梯（进阶）代码随想录题解：70. 爬楼梯（进阶）解题思路：这道题要求每次可以爬1-m层的楼梯，最终爬到n，相当于完全背包问题中，有无限个重量为1-m的物品，每次可以取不同重量的物品，要求最后重量加起来等于n时有多少种排列。那这题就跟组合总和IV是一样的了，就是完全背包+排列，因此

代码随想录算法训练营第四十四天| LeetCode70. 爬楼梯（进阶）、322. 零钱兑换、279.完全平方数

一、LeetCode 70. 爬楼梯（进阶）题目链接/文章讲解/视频讲解：https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85%E7%89%88%E6%9C%AC.html 状态：已解决 1.思路这道题跟70.爬楼梯 - 力扣

每日OJ题_完全背包②_力扣322. 零钱兑换

目录力扣322. 零钱兑换问题解析解析代码优化代码（滚动数组）力扣322. 零钱兑换 322. 零钱兑换难度中等给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。示例

动态规划专练（ 322.零钱兑换）

322.零钱兑换给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。示例 1：输入：coins = [1, 2, 5], amount = 11输出：3 解释：11 = 5 + 5 + 1 示例

leetcode 322

leetcode 322 题目例子思路记忆化搜索，使用数组，记录val的最少硬币数量；递归加bfs; 代码实现 #include <vector>#include <climits> // For INT_MAX#include <algorithm> // For minclass Solution {public:int step = 0;std::vecto

【Leetcode 322】零钱兑换 —— 动态规划

322. 零钱兑换给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。示例 1：输入：coins = [1, 2, 5], amount = 11 输出：3 解释：11 = 5 + 5 + 1

【LeetCode热题100】322. 零钱兑换（动态规划）

一.题目要求给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的。二.题目难度中等三.输入样例示例 1：输入：coins = [1, 2, 5], amount = 11 输出：3 解释：11 =

代码随想录算法训练营三刷 day45 | 动态规划之 70. 爬楼梯（进阶） 322. 零钱兑换 279.完全平方数

三刷day45 70. 爬楼梯（进阶）1. 确定dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例来推导dp数组 322. 零钱兑换1. 确定dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组 279.完全平方数1. 确定dp数组（dp table）以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍