【Leetcode 322】零钱兑换 —

【Leetcode 322】零钱兑换 —— 动态规划

本文主要是介绍【Leetcode 322】零钱兑换 —— 动态规划，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

322. 零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11
输出：3
解释：11 = 5 + 5 + 1

示例 2：

输入：coins = [2], amount = 3
输出：-1

示例 3：

输入：coins = [1], amount = 0
输出：0

题目分析

经典动态规划问题，更多案例可见 Leetcode 动态规划详解

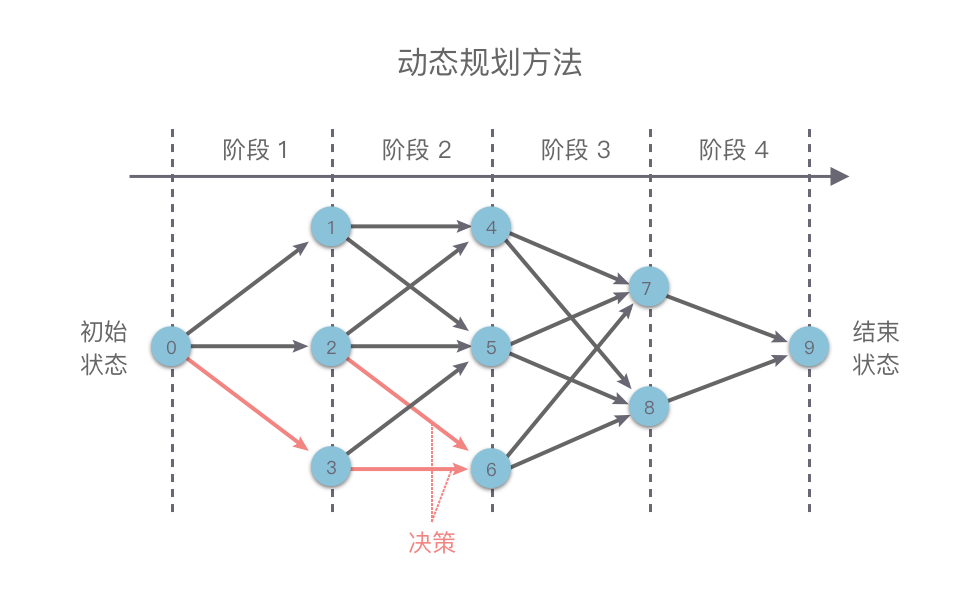
我们可以使用动态规划解决本题，解题思路：

状态定义：dp[i]为组成金额 i 所需最少的硬币数量
状态转移方程：枚举 j，需要从dp[i - coins[j] 转移过来，再算上枚举的这枚硬币数量 1 的贡献，由于要硬币数量最少，所以 dp(i) 为前面能转移过来的状态的最小值加上枚举的硬币数量 1

$dp[i] = min_{j=0..n-1}(dp[i - coins[j])$

初始状态dp[0] = coins[0]，最终答案为dp[amount]

coins = [1, 2, 3], amount = 6

动态规划一般用于求解具有重叠子问题和最优子结构的问题，例如最长公共子序列、背包问题、最短路径等。重叠子问题指的是在求解问题的过程中，多次用到相同的子问题，最优子结构指的是问题的最优解可以通过子问题的最优解来构造

public class Solution {public int coinChange(int[] coins, int amount) {int max = amount + 1;int[] dp = new int[amount + 1];Arrays.fill(dp, max);dp[0] = 0;for (int i = 1; i <= amount; i++) {for (int j = 0; j < coins.length; j++) {if (coins[j] <= i) {dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);}}}return dp[amount] > amount ? -1 : dp[amount];}
}