蒙特卡洛专题

应届生入职练手习题-蒙特卡洛算法(1.5H)

应届生入职练手习题 [编辑] 模拟射击，根据命中概率来求PI 要求：假设有一个半径为1000的圆形靶子（具体单位没有意义，不用写），我们随意对其进行射击，那么，统计所有落在圆形外接正方形中的弹着点，可以很容易得知：命中这个圆形靶子的概率是圆形的面积与外接方形面积的比目的：检验编程风格和实现效率要解这个题目就得有对蒙特卡洛算法的了解，原理如下在数值积分法中，利用求单位圆的1/4的面积

蒙特卡洛法之MATLAB实现

by WC 1.7.2016 蒙特卡洛法（随机取样法）也称为计算机随机模拟方法，它源于世界著名的赌城——Monte Carlo。它是基于对大量事件的统计结果来实现一些确定性问题的计算。使用蒙特卡洛法必须使用计算机

【算法】蒙特卡洛模拟

一、引言蒙特卡洛模拟算法是一种基于概率和统计理论的数值计算方法，通过随机抽样来近似复杂系统的概率问题。它以摩纳哥著名的赌场蒙特卡洛命名，象征着其基于随机性的特点。二、算法原理蒙特卡洛模拟算法的核心思想是利用随机抽样来估计一个函数的期望值或者某个概率分布的特性。它通过以下步骤进行：定义问题的随机变量和概率分布。随机生成大量的样本数据。对样本数据进行

蒙特卡洛模拟计算圆周率和积分

蒙特卡洛模拟计算圆周率 import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom matplotlib.patches import Circlen = 1000r = 1.0a,b = (0.0,0.0)xmin,xmax = a-r,a+rymin,ymax = b-r,b+rx = np.

深入探索蒙特卡洛树搜索（MCTS）：原理、应用与优化

深入探索蒙特卡洛树搜索（MCTS）：原理、应用与优化引言在人工智能与游戏开发领域，蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS）作为一种高效的启发式搜索算法，凭借其卓越的性能和广泛的应用前景，引起了业界的广泛关注。本文旨在深入探讨MCTS的基本原理、核心机制、应用领域以及优化策略，为读者提供一份详尽的技术指南。 MCTS基本原理定义与核心思想 MC

【数值计算方法】蒙特卡洛方法积分的Python实现

原文：https://www.cnblogs.com/aksoam/p/18378332 原理不做赘述,参见【数值计算方法】数值积分&微分-python实现 - FE-有限元鹰 - 博客园,直接上代码,只实现1d,2d积分,N维积分的蒙特卡洛方法也类似. 代码 from typing import Callable,Union,Listdef MonteCarloInt2d(f:Calla

lammps蒙特卡洛MC模拟案例

大家好，我是小马老师。本文介绍lammps和蒙特卡洛(MC)相结合的模拟方法。 MC是一种随机模拟方法，可以模拟一定区域内的随机原子交换过程。在lammps中，和MC相关的模拟命令有三个：fix gcmc、fix atom/swap、fix sgcmc。本文主要介绍fix sgcmc命令。sgcmc命令可应用到合金的模拟中，如短程有序模拟。 fix sgcmc语法格式： fix ID gro

▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch5 蒙特卡洛方法【model-based ——＞ model-free】

PPT 截取必要信息。课程网站做习题。总体 MOOC 过一遍 1、视频 + 学堂在线习题 2、过电子书是否遗漏【下载：本章 PDF GitHub 页面链接】【第二轮才整理的，忘光了。。。又看了一遍视频】 3、过 MOOC 习题看 PDF 迷迷糊糊，恍恍惚惚。学堂在线课程页面链接中国大学MOOC 课程页面链接 B 站视频链接 PPT和书籍下载网址：【Gi

使用Metropolis蒙特卡洛方法的原子模拟

文章目录 1.蒙特卡罗方法的目标2.热力学系综3.连续体系4.Metropolis算法1.Metropolis算法介绍2.Metropolis算法思路 5.原子体系的蒙特卡洛算法1.算法的基本思想2.算法的实现过程 1.蒙特卡罗方法的目标蒙特卡罗方法可以做什么？提供材料的热力学信息；评估整体的平均值（能量、压力等）。蒙特卡罗方法不能做什么？提供材料的动力学信息（例

MCT Self-Refine：创新集成蒙特卡洛树搜索（MCTS）提高复杂数学推理任务的性能，超GPT4，使用 LLaMa-3 8B 进行自我优化

📜 文献卡题目： Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine with LLaMa-3 8B作者: Di Zhang; Xiaoshui Huang; Dongzhan Zhou; Yuqiang Li; Wanli OuyangDOI: 10.48550/a

现代信号处理14_基于蒙特卡洛的信号处理（CSDN_20240616）

Monte Carlo/Simulation方法在统计上，样本数量是一个很重要的问题，在处理问题（如计算样本均值）的过程中，样本数量越多越好。但是在实际中，样本往往是稀缺的，获取数据就要付出代价。在贝叶斯理论中，情况又有所变化，X作为样本数据，其数量似乎不会影响问题的分析，因为我们产生的伪随机数是服从分布fθX 的，理论上只要能够产生这样的随机数，那么随机数的个数完全由我们自己决定。即

python 学习蒙特卡洛求π DAY9

import random import math import time s = eval(input("请输入取点总数：")) hits = 0.0 start = time.perf_counter() for i in range(s): x,y = random.random(),random.random() dist = math.sqrt

蒙特卡洛方法近似计算圆周率

一、原理图正方形区域内有1/4圆区域，向区域内随机大量掷点。根据概率论知识，落在每一点的概率相等，当n无限大时，落在1/4区域内的点占总点数量的比例即1/4圆占正方形面积的比例，圆周率PI=4（N1/N）[N1:落在1/4圆中点的数量，N:总点数]。二、c++试验 #include <iostream>#include <random>#include <cmath>#i

强化学习(四) 蒙特卡洛方法

如果算不出来，那就统计。 dp需要完备的环境模型，而蒙特卡洛方法不需要。后者只需要采样。或者说，经验。此外，蒙特卡洛方法不是自举的，不通过其它价值估计来更新自己的价值估计（与dp不同）。不满足马尔可夫性时仍可用。蒙特卡洛不是在线的，而是在一幕结束后才进行调整。蒙特卡洛方法做了一件什么事？求q派(s,a)。求出来相当于完成了策略评估，完成之后使用广义策略迭代来改进策略，跟dp一样。

蒙特卡洛法求解机械臂工作空间（以IRB4600型工业机械臂为例）

1. 概念工作空间是衡量机器人工作能力的一个重要的运动学指标，蒙特卡洛法是一种随机模拟方法，用于在计算机上估计某些统计量，对于要估计的统计量，通过模拟大量的随机抽样，并计算这些样本的随机值来估算这个统计量的值。蒙特卡洛法的优点在于，在处理许多复杂的问题时可以通过模拟来估计答案，而无需解决复杂的数学方程。 2. 蒙特卡洛法求解蒙特卡洛法求解机械臂工作空间流程是将各个关节在限位范围内离散后

【数学建模】自动化车床管理(蒙特卡洛模拟法)

1999年全国大学生数学建模竞赛题目A question1假设检验建立模型重新建立模型随机化求解自动化车床管理一道工序用自动化车床连续加工某种零件，由于刀具损坏等原因该工序会出现故障，其中刀具损坏故障占 95%, 其它故障仅占 5%。工序出现故障是完全随机的, 假定在生产任一零件时出现故障的机会均相同。工作人员通过检查零件来确定工序是否出现故障。现积累有 10

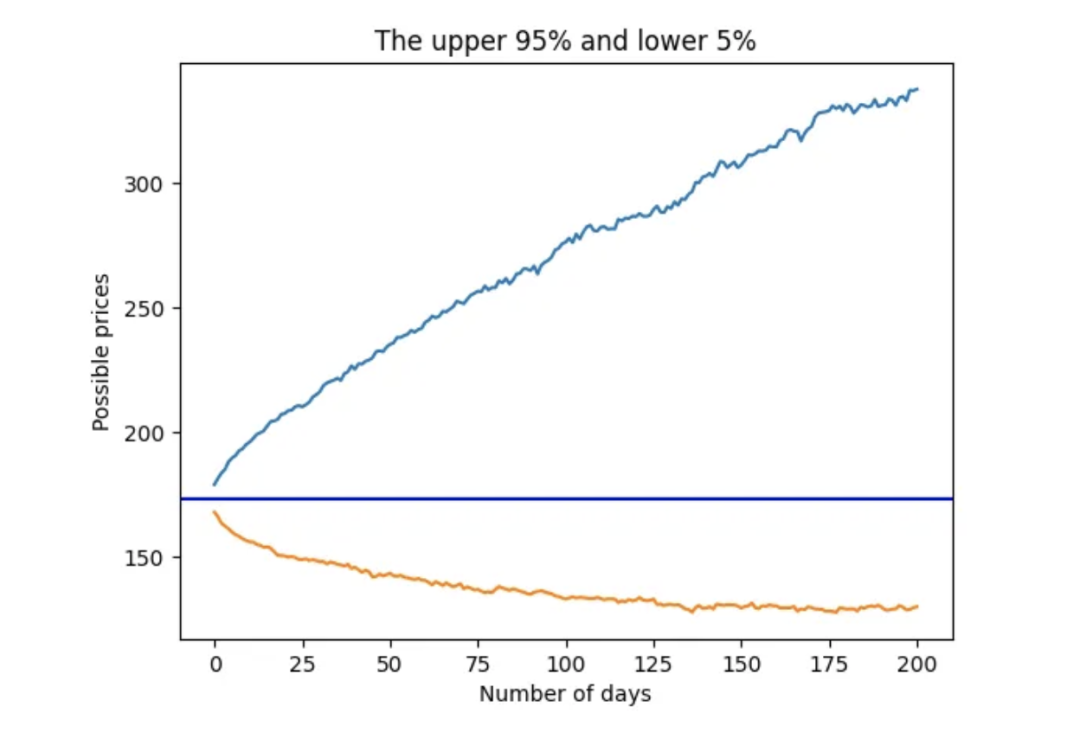
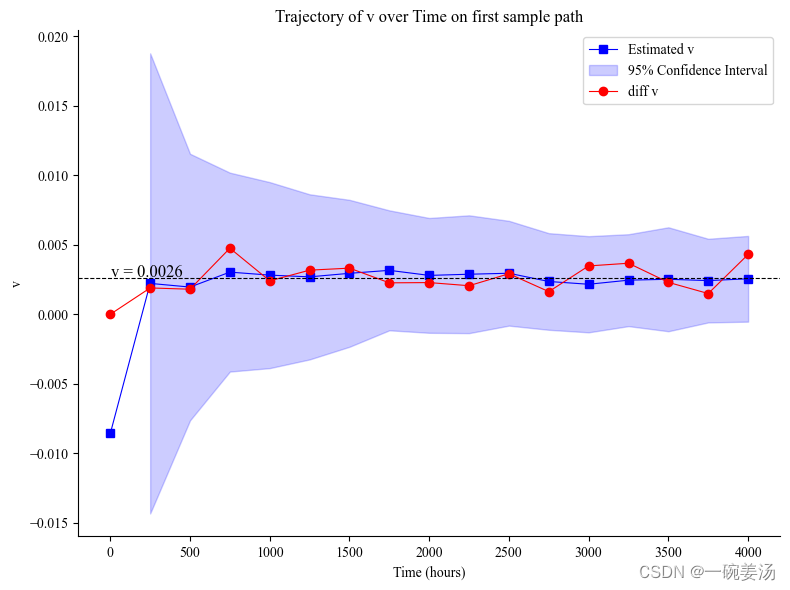
用于时间序列概率预测的蒙特卡洛模拟

大家好，蒙特卡洛模拟是一种广泛应用于各个领域的计算技术，它通过从概率分布中随机抽取大量样本，并对结果进行统计分析，从而模拟复杂系统的行为。这种技术具有很强的适用性，在金融建模、工程设计、物理模拟、运筹优化以及风险管理等领域都有广泛的应用。蒙特卡洛模拟这个名称源自于摩纳哥王国的蒙特卡洛城市，这里曾经是世界著名的赌博天堂。在20世纪40年代，著名科学家乌拉姆和冯·诺依曼参与了曼哈顿计划，他们需要解

蒙特卡洛求PI（抛点法）TypeScript实现

解决node先console.log不能用 pnpm install -D tslib @types/node tsconfig.json {"compilerOptions": {"target": "es2020","module": "commonjs","lib": ["es2020"],"sourceMap": true,"outDir": "./dist","rootDir":

蒙特卡洛电动汽车负荷预测

部分代码： P_load=load('load.txt'); P_load=P_load/100000; B=EV_load(958); %每个节点接入1250辆电动汽车接入位置8 14 29 for i=1:24 [Ploss,V]=IEEE33(B(i),P_load(i)); Ploss_after(i)=Ploss; V_after(i,:)=V; end for i=1:

粒子滤波（序贯蒙特卡洛）及其python实现

粒子滤波（序贯蒙特卡洛）及其python实现一、原理讲解二、实证分析参考视频：现代数字信号处理II_张颢授课教师：张颢 2020-2021学年（春）第二学期（第20集）一、原理讲解序贯的蒙特卡罗，这是一个什么问题呢？现在我们考虑这样的模型：这是一种所谓叫做状态空间模型也有人管这个东西叫隐马尔可夫模型，说的是一个意思。就是现在，我们有一条马尔可夫链，然后这里头

【物理应用】基于matlab非序贯蒙特卡洛法评估风电系统【含matlab源码 766期】

⛄一、获取代码方式获取代码方式1：完整代码已上传我的资源：【物理应用】基于matlab非序贯蒙特卡洛法评估风电系统【含matlab源码 766期】点击上面蓝色字体，直接付费下载，即可。获取代码方式2：付费专栏Matlab物理应用（初级版）备注：点击上面蓝色字体付费专栏Matlab物理应用（初级版），扫描上面二维码，付费29.9元订阅海神之光博客付费专栏Matlab物理应用（初级

【优化充电】基于matlab蒙特卡洛算法求解电动汽车充电优化问题【含Matlab源码 1164期】

⛄一、获取代码方式获取代码方式1：完整代码已上传我的资源：【优化充电】基于matlab蒙特卡洛算法求解电动汽车充电优化问题【含Matlab源码 1164期】点击上面蓝色字体，直接付费下载，即可。获取代码方式2：付费专栏Matlab优化求解（初级版）备注：点击上面蓝色字体付费专栏Matlab优化求解（初级版），扫描上面二维码，付费29.9元订阅海神之光博客付费专栏Matlab优化

蒙特卡洛方法【强化学习】

强化学习笔记主要基于b站西湖大学赵世钰老师的【强化学习的数学原理】课程，个人觉得赵老师的课件深入浅出，很适合入门. 第一章强化学习基本概念第二章贝尔曼方程第三章贝尔曼最优方程第四章值迭代和策略迭代第五章强化学习实践—GridWorld 第六章蒙特卡洛方法文章目录强化学习笔记一、 Motivating example二、 MC-Basic method三、

蒙特卡洛光线追踪蒙特卡洛积分基础知识三

蒙特卡洛光线追踪技术系列见蒙特卡洛光线追踪技术多维蒙特卡罗积分将前面的等式应用于多维积分是很简单的，除了选择多维采样点可能比一维情况更复杂。作为二维中的一个例子，假设我们想在原点中心的正方形 [-1，1]^2 上积分一些函数 f 。这可以记为单个二维变量x上的积分：在每个 xi 是二维点分布的二维密度P。我们可以转换成更明确的笛卡尔坐标，并且有一种形式，我们可能更舒服：

蒙特卡洛光线追踪（准）蒙特卡洛积分基础知识二

蒙特卡洛光线追踪技术系列见蒙特卡洛光线追踪技术估计方法：许多问题涉及独立随机变量xi的和，其中变量共享一个公共密度p。这些变量被称为独立同分布（iid）随机变量。当和除以变量数时，我们得到E(x)的估计：随着N的增加，这个估计的方差减小。我们希望N足够大，我们有信心估计“足够接近”。然而，在蒙特卡罗中并没有确定的东西；我们只是得到统计上的信心，我们的估计是好的。可以肯定的是，我

蒙特卡洛光线追踪简介和基础知识基础知识一

蒙特卡洛光线追踪技术系列见蒙特卡洛光线追踪技术蒙特卡洛光线追踪的介绍：真实感图像合成在娱乐（电影、特效和游戏）、设计、建筑等领域越来越重要。在所有这些领域中，一个共同的趋势是要求越来越复杂的模型具有更真实的图像。基于蒙特卡罗射线追踪的技术是唯一能够处理这种复杂性的方法。算法和计算能力的最新进展使得蒙特卡罗射线追踪成为大多数问题的自然选择。这与几年前（有限元）光能传递方法是大多数图形研究