本文主要是介绍现代信号处理14_基于蒙特卡洛的信号处理（CSDN_20240616），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
Monte Carlo/Simulation方法
在统计上，样本数量是一个很重要的问题，在处理问题（如计算样本均值）的过程中，样本数量越多越好。但是在实际中，样本往往是稀缺的，获取数据就要付出代价。在贝叶斯理论中，情况又有所变化，X作为样本数据，其数量似乎不会影响问题的分析，因为我们产生的伪随机数是服从分布fθX 的，理论上只要能够产生这样的随机数，那么随机数的个数完全由我们自己决定。即贝叶斯理论中，样本数量没有限制，但是我们得到的最终结果并不一定随着伪随机样本的增多而越来越好。因为伪随机数是根据模型fθX 产生的，样本数据X的数量直接决定模型的质量，如果模型不够好，最终的伪随机数也不会太好。
只有一个样本数据的Monte Carlo方法的例子
通过上面的分析，我们可以知道，原则上只要有一个样本就可以对未知参数进行估计了，下面用例子说明。
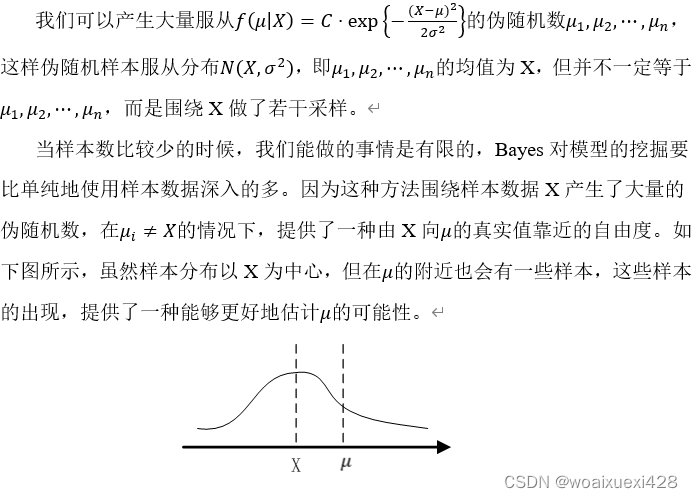
正是因为这种可能性，我们不再把数据看得那么死板，并在采样数据的基础上得到了新的随机性，这样的数据可以弥补采样数据的不足。采样数据无论有多少，都不能包含这个随机变量的全部信息，因此这种有贝叶斯方法引入的新的随机性有重要作用。
如果还有关于未知参数的先验分布，我们往往还能可以得到更好的结果。
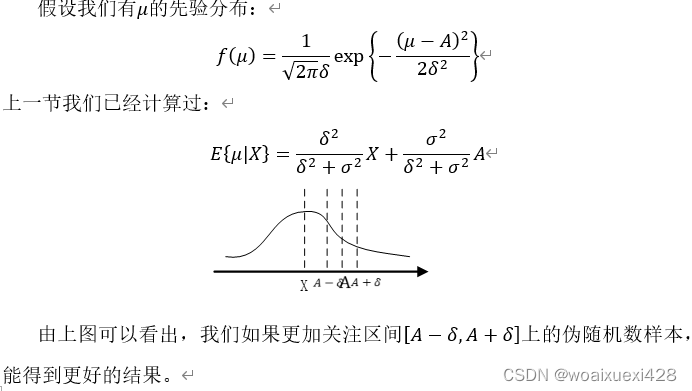
由上面的分析可以看出，我们对样本数据X的依赖性改变了：不再是拿到数据后就去做估计，而是用贝叶斯理论去分析，我们发现，无论这个样本是否准确，总会有一些伪随机数会延伸到真值附近。如果有先验知识，就可以更加接近真实值，而这种接近是不需要样本的帮助的。
构造伪随机数的方法1
构造[0,1]上均匀分布的随机数
计算F-1
构造服从高斯分布的伪随机数
中心极限定理
极方法（Polar Method）
构造服从瑞利分布的伪随机数
重要采样（Important Sampling）
通过重要采样方法，我们可以构造一些简单的σ2 的函数的随机数，对于一些比较复杂的函数，这种方法也有些无能无力。
我们使用Monte Carlo方法研究问题时，样本数据并没有直接使用，而是放在后验分布模型中，伪随机数是由我们自己决定的。当伪随机数无法直接产生时，可以使用重要采样，绕过难以产生的伪随机数，以相对容易的分布为桥梁，简介产生需要的伪随机数。
基于Markov链的Monte Carlo（Markov Chain Monte Carlo, MCMC）
Markov链
马氏链有很多状态，且它的状态在不断地转移，样本在每个状态上都会有所停留，停留时间有长有短（或者访问次数有多又少），最终的分布就体现了访问某个状态的次数在总的转移次数中的占比，这就是极限分布。
如果极限分布π 存在，（存在的条件：不可约、非周期、正常反），那么
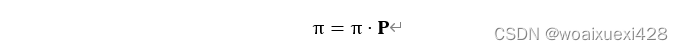
细致平衡（Detailed Balance）
Metropolis-Hastings算法
------------------------------------------------------------------------------------------------
因为文档中公式较多，不方便编辑，所以本文使用截图的方式展现。如需电子版文档，可以通过下面的链接进行下载。
链接
http://generatelink.xam.ink/change/makeurl/changeurl/11782
这篇关于现代信号处理14_基于蒙特卡洛的信号处理（CSDN_20240616）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
