粒子滤波（序贯蒙特卡洛）及其python实现

本文主要是介绍粒子滤波（序贯蒙特卡洛）及其python实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

参考视频：现代数字信号处理II_张颢 授课教师：张颢 2020-2021学年（春）第二学期（第20集）

一、原理讲解

序贯的蒙特卡罗，这是一个什么问题呢？现在我们考虑这样的模型：这是一种所谓叫做状态空间模型也有人管这个东西叫隐马尔可夫模型，说的是一个意思。
就是现在，我们有一条马尔可夫链，然后这里头的每一个状态都有一系列的取值。每一个状态针对的是某一时刻的情况，所以说它是带有时间信息的，同时我们也称之为叫做序贯的。
那么这个马尔可夫链有什么特点呢？就是它的这个所谓叫做状态呀，是直接观测不到的。
你能够拿到的，只有和状态有关的这些观测值，换句话讲我们知道的是 Y 1 : n = { Y 1 , . . . , Y n } Y_{1:n}=\{Y_1,...,Y_n\} Y1:n​={Y1​,...,Yn​}我们不知道的是 X 1 : n = { X 1 , . . . , X n } X_{1:n}=\{X_1,...,X_n\} X1:n​={X1​,...,Xn​}好我们需要做什么？我们需要由这个观测，去推算我们的状态。换句话说我们希望，用Y去估计X：$$Y_{1:n}\Rightarrow X_{1:n}$$这意味着我们所关注的也就是这么一个后验概率：$$P(X_{1:n}|Y_{1:n})\text{\hspace{1em}(1)}$$这个后验概率啊，它很有特点：这里面，它放在条件位置的是我们的观测量$Y_{1:n}$，而放在被推断对象位置的，是我们的状态量$X_{1:n}$，我们用已知的观测量去推断我们未知的状态量，这是我们要干的事情。现在我们来考察它这个后验分布，我们按照我们目前已经学到的知识，对他大概有两种处理：

一种处理是，我直接从它身上进行采样，就不管我用接受拒绝也好，还是MCMC也好，我可以直接对它进行采样，没问题吧？那么，这个采样啊，有毛病。大家知道这个毛病在哪吗？

注意！我如果采样的话我采样的是一个随机矢量，它的长度为n。那么如果我的n发生了变化，就好像我在这个时刻是n时刻，然后我到了n+1时刻的时候，我们的分布变成了这个样子：$$P(X_{1:n+1}|Y_{1:n+1})\text{\hspace{1em}(2)}$$那么我有没有可能，把已有的采样都用上，然后去得到我们新的采样？换句话讲，我是不是可以把它写成，前头我已经做过的一个采样，然后再加上n+1的第k个采样值，我能这么写吗？$$X_{1:n+1}^{(k)}=(X_{1:n}^{(k)},X_{n+1}^{(k)})$$通常是不行的。为什么不行？是因为我(1)、(2)这两个概率：一个是n个变量的联合概率分布，一个是n+1个变量的联合概率分布，这两个联合概率分布他们可能从本质上就是不同的。所以我是没有办法说把前面的样本，给它保留下来。因为我这个新的这个联合概率分布里面，从1到n这一部分样本它们的关联关系与我老的这个分布的这个关联关系多半是不一样的。所以我没有办法把老的这一部分的数据可以给保留下来，只去做新的，这件事我做不到。

无论是我用mcmc也好还是用接受拒绝也好，我直接去做采样，都没有办法实现我在时序上的
一个递推。换句话说这里头是没有递推的。因此我们需要来考虑另一条路，所谓的重要采样。

那么重要采样是这样的，我的目标分布是$p(x)$，然后我需要去做的，是所谓贝叶斯计算：$$p(x)\to {\int }_{-\infty }^{+\infty }p(x)f(x)dx=E_p[f(x)]\text{\hspace{1em}(3)}$$
也就是说，以$p(x)$作为分布的，$f(x)$的这么一个期望。然后我把这件事啊，给它转成了这么一个样子：$$\Rightarrow {\int }_{-\infty }^{+\infty }f(x)\frac{p(x)}{q(x)}q(x)dx\text{\hspace{1em}(4)}$$然后我试图来计算这个积分。我为什么试图计算这个积分呢？是因为，这个$q(x)$是一个比较容易采样的这么一个分布。也就是说，我可以采出来若干个样本 $x^{(1)},...,x^{(N)}\sim q(\cdot )$ 然后我就可以将这个积分看作是以 $q$ 作为分布的这么一个东西的积分：$${\int }_{-\infty }^{+\infty }f(x)\frac{p(x)}{q(x)}q(x)dx=E_q[f(x)\frac{p(x)}{q(x)}]\text{\hspace{1em}(5)}$$它就约等于：$$\approx \frac{1}{N}\sum _{k=1}^{N}f(x^{(k)})\frac{p(x^{(k)})}{q(x^{(k)})}\text{\hspace{1em}(6)}$$看看我是不是能够用这么一个蒙特卡罗的方法来逼近我们的期望啊。

好！我们的故事就从这儿开始。我们为什么说重要采样是有利于我们去找到时间上的递推关系的？这是有原因的。我们发现直接进行伪随机数的发生会导致时间上的递推关系很难做，因为我们已经做过的计算，没法给它保留下来。但是重要采样，后续你会看到，可以自然地做到这样的保留。

我们的分析就从（6）开始，我们把这个求和改写一下：$$\sum _{k=1}^{N}f(x^{(k)})\left[\frac{1}{N}\frac{p(x^{(k)})}{q(x^{(k)})}\right]\text{\hspace{1em}(7)}$$我们把$\frac{1}{N}$拿进来，然后我把这一部分设成$w_k$：
$$\frac{1}{N}\frac{p(x^{(k)})}{q(x^{(k)})}\to w^{(k)}\text{\hspace{1em}(8)}$$然后我就可以把它进而写成$w_k$的样子：$$\Rightarrow \sum _{k=1}^{N}f(x^{(k)})w^{(k)}\text{\hspace{1em}(9)}$$注意！这个$w_k$我们有一个说法，我们管它叫Weight，也有人管它叫粒子（Particle）。待会我们还会解释一下这个说法，这么一来我们的计算目标就写成了（8）这个样子。

然后呢，我们的分布实际上就变成了这么一个样子：$$p^{\ast }(x)=\sum _{k=1}^N\delta (x-x^{(k)})w^{(k)}\text{\hspace{1em}(10)}$$这是一个新的分布，大家注意看这个分布是一个什么样的形式？——它是一个离散分布：这个分布只在这些$x^{(k)}$上取值，然后每一个$x^{(k)}$上取值的概率相当于是这个$w_k$没问题吧。

只不过这个分布有一点毛病，什么毛病呢？我并不能确保这个$p^{\ast }(x)$它一定是一个分布，尽管（8）能看出来它一定是个非负的，但是他加起来不一定等于1，所以我们怎么办？那没问题！我们归一化就行了。
我们归一化就行了：$$\begin{gathered} {\int }_{-\infty }^{+\infty }{p}^{\ast }(x)dx=\sum _{k=1}^N{\int }_{-\infty }^{+\infty }\delta (x-x^{(k)})w^{(k)}dx \\ =\sum _{k=1}^N{w}^{(k)}=Z\text{\hspace{1em}(11)} \end{gathered}$$我们再让：$$p^{\ast }(x)=\frac{1}{Z}\sum _{k=1}^N\delta (x-x^{(k)})w^{(k)}\text{\hspace{1em}(12)}$$这样一来，$p^{\ast }(x)$就真的是一个分布了。我们进一步写成如下的形式：$$p^{\ast }(x)=\sum _{k=1}^N\delta (x-x^{(k)}){\hat{w}}^{(k)}\text{\hspace{1em}(13)}$$其中，${\hat{w}}^{(k)}=\frac{w^{(k)}}{Z}$，我们再把（9）写成这个形式：$$\sum _{k=1}^{N}f(x^{(k)})w^{(k)}=Z\cdot \sum _{k=1}^{N}f(x^{(k)}){\hat{w}}^{(k)}\text{\hspace{1em}(14)}$$这是我们对于重要采样的认识，但是我们还没有谈及问题的关键，下面我们准备来谈一谈，我们准备用重要采样来处理之前提到的隐马尔科夫模型。

此时我有这样的结果，我的目标分布就是我的这个后验分布：$$P(X_{1:n+1})=P(X_{1:n+1}|Y_{1:n+1})\text{\hspace{1em}(15)}$$然后呢，我准备重要采样，重要采样的关键是什么？重要采样关键是，当我计算任何一个 $f$ 的期望的时候，本质上都是在计算什么？我本质上都是在计算 $p^{\ast }$ 这么一个分布对于 $f$ 的期望： $$E_{p_{n+1}^{\ast }}[f(X_{1:n+1})]\to E_p[f(X_{1:n+1})]\text{\hspace{1em}(16)}$$我在这儿完成了一个什么转换呢？我从连续的积分，通过重要采样的样本总结出 $w$ 粒子，从而使得期望的计算转为了离散的求和。我们是在用离散分布近似我原先的这个分布。那么现在有意思的事儿要来了，就是我期望去获得一种时间上的递推： $$E_{p_n^{\ast }}[f(X_{1:n})]\to E_{p_{n+1}^{\ast }}[f(X_{1:n+1})]\text{\hspace{1em}(17)}$$又由于$p^{\ast }$是完全由 $\hat{w}$ 决定的。所以实际上是在做这么样一个递推：$${\hat{w}}_n\to {\hat{w}}_{n+1}$$因此我们现在之所以能够把这种时间上的递推关系在我们的重要采样上实现，它的本质就在于我们要把粒子 $\hat{w}$ 在不同时刻的，相互之间的演化关系搞清楚。

好下面我们就来搞清楚这个 $\hat{w}$ 究竟是什么情况，根据（8）我们实际上有：$${\hat{w}}_{n+1}\propto \frac{p(X_{1:n+1}|Y_{1:n+1})}{q(X_{1:n+1})}\propto \frac{p(X_{1:n+1},Y_{1:n+1})}{q(X_{1:n+1})}\text{\hspace{1em}(18)}$$${\hat{w}}_{n+1}$是归一化过的，我们之所以不写等号是因为它前头有一个因子，那个因字就不管它了，因为因子是个常数，第二步$\propto$是因为跟$Y$有关的采样数据的概率现在也是个常数。因此，对于 ${\hat{w}}_n$ 我们也有：$${\hat{w}}_n\propto \frac{p(X_{1:n},Y_{1:n+1})}{q(X_{1:n})}\text{\hspace{1em}(19)}$$有意思的事要来了。注意，原本我这里的q的选择，他都有各自的选取方式，我需要在每一个阶段选取一个q出来，然后把这一阶段的随机矢量都给采出来，采一个多维的随机矢量这件事本来就很难，那么我当然希望这个n维的随机矢量采出来以后这个结果可以直接帮助我n+1维的采样。但是之前说过因为两个阶段的分布结构可能是不一样的，所以还不能说随机矢量你只采n+1那一维，然后把剩下的1到n样本填充上去，这件事不符合随机采样的定义，所以，我们就没有办法在直接采样的基础上去形成递推。

但是我现在不在样本上，而是在这个分布上，注意这是两码事儿，一个是你这个随机样本，一个是随机样本所服从的分布。我目前只要找到两个分布计算的结果间的递推关系就可以了。我不需要具体到那个样本上，这样的话我这两个weight之间，就能形成递推，你看我怎么找到这个分布的递推关系。我们需要对隐马尔可夫有一定的认识：$$\begin{gathered} p(X_{1:n+1},Y_{1:n+1})=p(Y_{n+1}|X_{n+1},X_{1:n},Y_{1:n})p(X_{n+1}|X_{1:n},Y_{1:n})p(X_{1:n},Y_{1:n}) \\ =p(Y_{n+1}|X_{n+1})p(X_{n+1}|X_n)p(X_{1:n},Y_{1:n})\text{\hspace{1em}(20)} \end{gathered}$$

$$q(X_{1:n+1})=q(X_{n+1}|X_{1:n})q(X_{1:n})\text{\hspace{1em}(21)}$$

$$\begin{gathered} {\hat{w}}_{n+1}\propto \frac{p(Y_{n+1}|X_{n+1})p(X_{n+1}|X_n)p(X_{1:n},Y_{1:n})}{q(X_{n+1}|X_{1:n})q(X_{1:n})} \\ =\frac{p(Y_{n+1}|X_{n+1})p(X_{n+1}|X_n)}{q(X_{n+1}|X_{1:n})}{\hat{w}}_n\text{\hspace{1em}(22)} \end{gathered}$$这正是我们想要找的东西，这就是粒子随时间的演化规律，这就是粒子滤波（Particle Filter）

我们大家仔细看，在（22）这个演化当中，$X_{1:n}$和$Y_{n+1}$都是我知道的，我唯一不知道的是$X_{n+1}$，不知道我该怎么办？注意，我们是在做蒙特卡洛，所以我们是要以随机采样作为基础，你说这个$X_{n+1}$我不知道，我是不是可以把它采出来，我产生出它的伪随机数，我用哪个分布来产生？当然用 $q(X_{n+1}|X_{1:n})$ 了，你想想看这个 $q$ 是我比较明白的分布，所以我用 $q(X_{n+1}|X_{1:n})$ 来产生出 ${\hat{X}}_{n+1}$的样本。

注意，我们的focus不是在这些采样本身而是在这个粒子上，这个粒子不是那个样本本身，这个粒子是这些样本的分布值，这也是为什么我说从分布本身的角度去推演。

${\hat{X}}_{n+1}$采出来以后，我们就能形成这个粒子的随时间的推演，从而我们的贝叶斯积分随时间的演化也就应运而生。大家体会一下，这就是我们常说的 sequential 的蒙特卡洛。

我们summary一下啊，我们这个sequential的蒙特卡洛，两个要点：

1. 我们采用的是重要采用策略，我们为什么采用重要采样策略，解释过了再解释一遍，是因为如果我要直接去采随机样本，我很难在维度上进行迭代或者说进行演化。因为我n加一维的随机样本不能够把n维随机样本作为其中的n维先填充进来，只去采最后一维，这不行。这个与我们随机采样的基本定义是违背的，因此我就不能够直接采样。因为我们上节课所讲的三种方法里两种是跟直接采样有关，一个是接受拒绝，一个是MCMC，这两种，无论哪一种都不能用，因为他们都是直接采样，所以我们采用的是所谓重要采样。重要采样它不是直接采，我们一上来先对重要采样进行一个分析，我们分析的结果的核心实际上是我们把我们想要计算的这个积分，转化成了粒子进行加权求和，因此我们只要对粒子在不同时间上的迭代关系搞得很清楚就可以了，此其一。
2. 其二粒子在不同时间上的关系要想搞清楚的话，我们需要仔细的分析这个粒子的结构，而通过我们的分析我们发现，这个粒子结构里头包含有一系列的分布，这些分布反映的是我们隐马尔科夫模型或者说我们的状态空间模型的演化规律。那么在状态空间模型的演化规律得以有效利用的前提下我们发现，我们粒子里面所涉及到的这些分布，实际上是可以形成关于时间的递推，并且其中充分的用到了马尔可夫性，使得我们能够比较简单地将这两个因子$P(Y_{n+1}|X_{n+1})$、$P(X_{n+1}|X_n)$表达出来，而一旦这两个因子一表达出来，这个事儿就没问题了，剩下的我们发现它粒子之间的演化规律就来了。

前面这件事情我们，还可以做一点点解读，当然这种解读都不会是很全，都有一定的片面性但是能够帮助大家理解。这个粒子他如果要被强化，什么叫被强化，它如果变大意味着什么？它如果变大的话意味着在我n+1时刻，我的这个 $p^{\ast }$，以粒子作为权重的那个离散分布，某一个点的这个权重要得到加强，那么这个点的权重之所以得到加强的一部分原因就在于$P(Y_{n+1}|X_{n+1})$这个概率要大，这个概率大意味着我现有状态更好的支持了我的观测，这个状态你说我是不是应该更加的相信他是对的，因为我状态直接观测不到，我只有对他进行推断，那么假如他更好的支持我的观测，我是不是应该更加相信他是对的。因此这个状态，相关的粒子，我是不是就应该予以强调。那么他的权重就会有所增加，还是挺直观的。

这个滤波器就叫粒子滤波器，卡尔曼滤波器是粒子滤波的特例。我们上学期推卡曼滤波的时候用的是信息的策略，实际上我们推卡门滤波是可以从粒子滤波这个角度走，就是不外乎上面所有的分布我们全能写出来，因为这些东西都是高斯，如果全是高斯的话这个地儿我是能直接把它explicit算出来，算出来就是我们看到的kalman，没差别。所以它是粒子滤波的特例，而粒子滤波它适合处理非高斯，因为kalman滤波里面这个递推关系$X_{n+1}$是以$X_n$作为均值的某种高斯，然后$Y_n$与$X_n$之间这个递推也是个高斯的关系。那妥了，那前头这因子我可以算的一清二楚，因为如果是高斯的话他无外乎就是些二次型，那么我在那二次行车倒腾一下就ok了。但是如果不是高斯，因子这个地方有没有办法解析地写清楚，因此我们采用的方法是蒙特卡洛，就是我们去采样，这也是我们对付非高斯的一个核心思想，高斯的事情我们是可以解析算算明白的，我们在随机过程里也能让大家看到这个高斯的解析形式有多么好，但是非高斯你就算不了啊，你这些这些地方你都算不清楚，算不清楚无所谓！我们就sample一下。哦，什么是滤波？滤波的意思就是递推，递推就叫滤波，什么叫filter，就是已经知道$X_n$，向$X_{n+1}$做推断，这东西就叫滤波。

大家看看其实基本思想很清楚，粒子滤波是非常典型的非高斯处理，它充分的反映了非高斯的实质特性，如果是高斯我们就全算明白了，不是高斯，无所谓，sample就行。但是它粒子之间的滚动发展的这个关系，和高不高斯，没一毛钱联系。这个发展的关系完全来自于马尔可夫性。

2002-2003年左右这个粒子滤波，是一统天下的，在信号处理里面当时你要用卡尔曼滤波就显得很out，你如果不玩玩粒子滤波你就感觉根本没有懂什么叫做时间滤波，而且他这个词起的很好，你看他要叫weight的话他的话就显得很土，他叫粒子就显得非常高大上，感觉粒子物理都是都是这个呃玄妙的代名词，一开始我也听我说这东西是不是跟粒子物理有关系，后来我看明白以后，我才恍然大悟这绝对是个标题党，它跟粒子物理没有一分钱的关系，他就管这个玩意儿叫粒子，但是这就显得非常高大上。

二、实证分析

用到我的本科论文里，状态空间模型：$$X(t)=vt+\kappa B(vt)$$其中X(t)是我的退化观测数据，v是漂移项参数，B(·)是标准布朗运动，$\kappa$是扩散系数，一般看做一个常数，t是时间。粒子滤波算法的伪代码如下:

代码实现：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt# 全局字体设置
plt.rcParams['font.family'] = 'sans-serif'  # 指定字体家族
plt.rcParams['font.sans-serif'] = ['Times New Roman']  # 指定具体字体# 状态空间模型参数
kappa = 0.1  # 扩散系数
dt = 250  # 时间步长# 观测数据
X_obs = np.array([0, 0.4741, 0.9255, 2.1147, 2.7168, 3.511, 4.3415, 4.9076, 5.4782, 5.9925, 6.7224, 7.1303, 8.0006, 8.9193, 9.494, 9.8675, 10.9446])
t_obs = np.array([0, 250, 500, 750, 1000, 1250, 1500, 1750, 2000, 2250, 2500, 2750, 3000, 3250, 3500, 3750, 4000])# 粒子滤波参数
num_particles = 10000  # 粒子数量
num_timesteps = len(t_obs)  # 时间步数# 初始化粒子
v_particles = np.random.normal(0, 1, num_particles)# 存储估计结果和置信区间
v_estimates = []
v_lower_bounds = []
v_upper_bounds = []# 粒子滤波主循环
for t in range(num_timesteps):# 预测步骤v_particles += np.random.normal(0, kappa, num_particles)x_particles = v_particles * t_obs[t] + kappa * np.random.normal(0, np.sqrt(t_obs[t]), num_particles)# 更新步骤weights = np.exp(-0.5 * (x_particles - X_obs[t])**2)weights /= np.sum(weights)# 重采样resampled_indices = np.random.choice(num_particles, size=num_particles, p=weights)v_particles = v_particles[resampled_indices]# 估计参数vv_estimate = np.mean(v_particles)v_estimates.append(v_estimate)# 计算95%置信区间v_std = np.std(v_particles)v_lower_bound = v_estimate - 1.96 * v_stdv_upper_bound = v_estimate + 1.96 * v_stdv_lower_bounds.append(v_lower_bound)v_upper_bounds.append(v_upper_bound)# 绘制v随时间变化的轨迹图
plt.figure(figsize=(8, 6))
# 不展示边框
ax = plt.gca()
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)plt.plot(t_obs, v_estimates, 'b-', label='Estimated v', marker = 's',linewidth = 0.8)
plt.fill_between(t_obs[1:], v_lower_bounds[1:], v_upper_bounds[1:], color='b', alpha=0.2, label='95% Confidence Interval')
plt.plot(t_obs, [0]+list(np.diff(X_obs) / dt), marker='o', linestyle='-', color='red', label='diff v',linewidth = 0.8)
plt.xlabel('Time (hours)')
plt.ylabel('v')
plt.title('Trajectory of v over Time on first sample path')
plt.legend()
# plt.grid(True)# 绘制水平线
y_position = np.round(v_estimates[-1], 4)  # 在 y 轴位置 0.02 处绘制水平线
plt.axhline(y=y_position, color='black', linestyle='--', linewidth = 0.8)
plt.text(2, y_position + 0.0001, f'v = {y_position}', color='black', fontsize=12, va='baseline')plt.tight_layout()# 保存图像
# plt.savefig(plot_path)
plt.show()

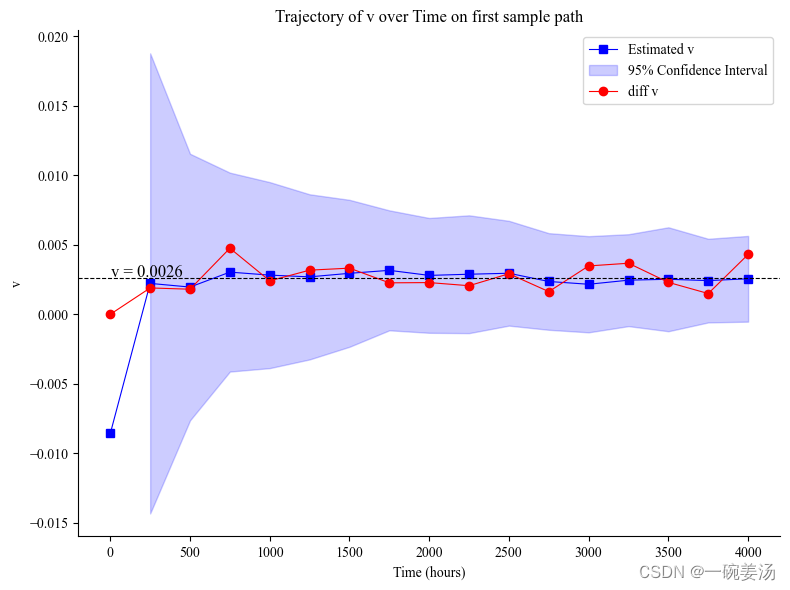
可以看出粒子滤波的估计方差正在逐渐缩小，并且相比于直接做差分，粒子滤波下的漂移项系数的估计值能够比较稳定，不会出现较大波动。

这篇关于粒子滤波（序贯蒙特卡洛）及其python实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---