本文主要是介绍蒙特卡洛光线追踪 (准)蒙特卡洛积分 基础知识二,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
蒙特卡洛光线追踪技术系列 见 蒙特卡洛光线追踪技术
估计方法:
许多问题涉及独立随机变量xi的和,其中变量共享一个公共密度p。这些变量被称为独立同分布(iid)随机变量。当和除以变量数时,我们得到E(x)的估计:
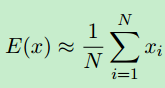
随着N的增加,这个估计的方差减小。我们希望N足够大,我们有信心估计“足够接近”。然而,在蒙特卡罗中并没有确定的东西;我们只是得到统计上的信心,我们的估计是好的。可以肯定的是,我们必须有n=∞。这种信心是用大数定律表示的:
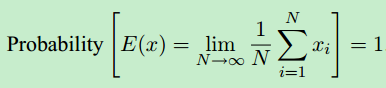
蒙特卡洛积分:
在这一节中,我们概述了定积分的基本蒙特卡罗解方法。然后这些技术直接应用于某些积分问题。本节的所有基本材料也包含在一些经典的蒙特卡罗文本中。这一部分的不同之处在于,它针对的是计算机图形学中出现的各种问题。对蒙特卡罗技术有兴趣的读者应该参考经典的蒙特卡罗文本之一[27,72,26,98]。
如前所述,给定一个函数f:S→R和一个随机变量x∼p,我们可以用和来近似f(x)的期望值:
 方程A
方程A
因为期望值可以表示为积分,所以积分也可以用和来近似。上面的方程的形式有点笨拙;我们通常希望近似于单个函数g的积分,而不是乘积fp。我们可以通过将g=fp替换为被积函数来解决这个问题:
 方程B
方程B
为了得到一个好的估计,我们需要尽可能多的样本,我们希望g/p有一个低方差(g和p应该有一个相似的形状)。智能地选择p称为重要抽样,因为如果p大,而g大,则在重要区域将有更多的样本。方程A也显示了蒙特卡罗积分的基本问题:收益递减。由于估计值的方差与1/N成正比,标准差与1/√N成正比。由于估计值中的误差与标准差的行为类似,我们需要将N乘以4才能将误差减半。
另一种减少方差的方法是将积分域S划分为几个较小的Si域,并将积分作为Si上的积分之和来计算。这叫做分层抽样。通常每个Si中只取一个样本(密度pi),在这种情况下,估计值的方差为:
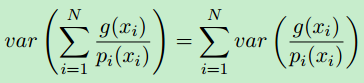
可以看出,如果所有层的测量值相等,分层抽样的方差永远不会高于非分层抽样的方差:
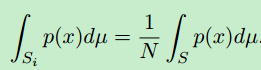
图形学中分层采样的最常见示例是像素采样的抖动。

![]()
由这个表,我们可以看出,通过分层采样,我们可以用比较少的采样个数让标准差得到较小的值。
作为区间(0,4)上积分I,设g(x)为x的蒙特卡罗解的一个例子:
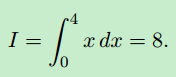
函数p的形状对N个样本估计的方差的巨大影响如上表所示。请注意,当p的形状与g的形状相似时,方差会减小。如果p=g/I,方差会降至零,但我们通常不知道,或者我们不必求助于蒙特卡罗。表所示的一个重要原则是,分层抽样往往远远优于重要抽样。虽然这种分层在I上的方差与样本数的立方成反比,但分层下的方差行为没有一般的结果。有些功能是分层不好的。一个例子是白噪声函数,其中所有区域的方差都是常数。另一方面,大多数函数将受益于分层抽样,因为每个子单元的方差通常小于整个域的方差。
总之要记住:分层抽样的效果会比较好。
准蒙特卡罗积分
尽管分布光线追踪通常被描述为方程B的应用,但许多研究者用更均匀分布(类星体)的样品(如[13,53])代替了ζi。这种方法可以被证明是正确的,通过分析减少误差的一些差异措施[99,97,53,67]而不是在方差方面。然而,通常使用随机样本的方差分析来制定采样策略,然后在实现中使用非随机、但均匀分布的样本。这种方法几乎可以肯定是正确的,但其理由和含义尚待解释。例如,当对[0,1]上的一维积分求值时,我们可以使用[0,1]上的一组N个均匀随机采样点(x1,x2,···,xN)来获得近似值:

有趣的是,我们可以用一组非随机点(y1,y2,···,yN)替换这些点(x1,x2,···,xN),近似仍然有效。如果这些点太规则,那么我们会产生混叠,但是这些点之间的相关性(例如,使用一维Poisson盘采样)不会使估计无效(仅使用Monte Carlo参数来证明近似值是正确的)。在某种意义上,这种准蒙特卡罗方法可以被认为是使用等分布点来估计 f 的高度。这与大多数数值分析文本中的传统数值积分求积方法(因为这些文本专注于一维问题)不符,但一旦你习惯了这个想法,你的直觉就不会变差。
Monte Carlo相对于QMC(准蒙特卡洛算法)在图形方面的相对优势仍然是一个悬而未决的问题。在某些条件下,QMC确实有更好的收敛性,但这些条件在图形中往往不成立。此外,在实践中很少有足够的样本用于渐近分析。为了使问题进一步复杂化,QMC有时会产生别名。然而,这种混叠有时在视觉上并不令人反感,因为它通常比传统蒙特卡罗方法产生的噪声要好。有关此主题的更多信息,请参阅Alexander Keller最近的工作。
这篇关于蒙特卡洛光线追踪 (准)蒙特卡洛积分 基础知识二的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







