积分专题

微积分-积分应用5.4（功）

术语“功”在日常语言中用来表示完成一项任务所需的总努力量。在物理学中，它有一个依赖于“力”概念的技术含义。直观上，你可以将力理解为对物体的推或拉——例如，一个书本在桌面上的水平推动，或者地球对球的向下拉力。一般来说，如果一个物体沿着一条直线运动，位置函数为 s ( t ) s(t) s(t)，那么物体上的力 F F F（与运动方向相同）由牛顿第二运动定律给出，等于物体的质量 m m m 与其

变速积分PID控制算法

变速积分PID控制算法变速积分PID控制算法：变速积分PID的基本思想：变速积分的PID积分项表达式：注：本文内容摘自《先进PID控制MATLAB仿真（第4版）》刘金琨编著，研读此书受益匪浅，感谢作者！变速积分PID控制算法：在普通的PID控制算法中，由于积分系数 k i k_i ki是常数，所以在整个控制过程中，积分增量不变。而系统对积分项的要求是，系统偏差大

梯形积分PID控制算法

梯形积分PID控制算法梯形积分PID控制算法: 注：本文内容摘自《先进PID控制MATLAB仿真（第4版）》刘金琨编著，研读此书受益匪浅，感谢作者！梯形积分PID控制算法: 在PID控制律中积分项的作用是消除余差，为了减小余差，应提高积分项的运算精度，为此，可将矩形积分改为梯形积分。梯形积分的计算公式： ∫ 0 t e ( t ) d t = ∑ i = 0 k e

抗积分饱和PID控制算法

抗积分饱和PID控制算法抗积分饱和PID控制算法:1.积分饱和现象：2.抗积分饱和算法：注：本文内容摘自《先进PID控制MATLAB仿真（第4版）》刘金琨编著，研读此书受益匪浅，感谢作者！抗积分饱和PID控制算法: 1.积分饱和现象：所谓积分饱和现象是指若系统存在一个方向偏差，PID控制器的输出由于积分作用的不断累加而加大，从而导致执行机构到达极限位置 X m

积分分离PID控制算法

积分分离PID控制算法积分分离PID控制：积分分离控制基本思路：积分分离控制算法表示：积分分离式PID控制算法程序流程图：注：本文内容摘自《先进PID控制MATLAB仿真（第4版）》刘金琨编著，研读此书受益匪浅，感谢作者！积分分离PID控制：在普通的PID控制中引入积分环节的目的，主要为了消除静差，提高控制精度。但在过程启动、结束或大幅度增减设定时，短时间内系统输出

c++求积分算法

//c++ 作业：用两重菜单显示积分函数和积分方法#include<iostream>#include<cmath>using namespace std;class Function{public:virtual double operator()(double x) const=0; };class Function1:public Function{publi

离散的点进行积分

1，可以直接用梯形公式 % 定义x和y坐标向量x = [0, 1, 2, 3, 4, 5]; % x的值y = [0, sin(1), sin(2), sin(3), sin(4), sin(5)]; % y的值，这里假设y是sin函数在x处的值% 使用trapz函数计算数值积分integral_value = trapz(x, y);% 显示结果disp(['The numerical

积分直方图(Integralnbsp;Histog…

原文地址：积分直方图(Integral Histogram) 作者：小罗积分直方图是有Fatih Porikli在CVPR-2005《Integral Histogram: A Fast Way to Extract Histograms in Cartesian Spaces》的论文中提到的。在介绍积分直方图之前，先介绍下积分图像，积分图像是P.Viola and

导数和积分的转换关系

纯积分的磁链观测器

纯积分的磁链观测器文章目录纯积分的磁链观测器1. 基本概念2. 计算转子角度的公式3. C语言实现4. 代码解释5. 实际应用中的注意事项6. 总结 1. 基本概念磁链（Flux Linkage）是指磁通量和绕组匝数的乘积，在电机控制中，通常讨论的是定子磁链或转子磁链。对于永磁同步电机（PMSM），磁链的动态方程通常可以表示为： λ s = ∫ ( V s − R

带衰减因子的积分磁链观测器

带衰减因子的积分磁链观测器文章目录带衰减因子的积分磁链观测器1. 背景问题2. 带衰减因子的积分器3. 理解公式4. 实现带衰减因子的积分器5. C语言代码实现6. 代码解释7. 带衰减因子的积分器的优点8. 实际应用中的考虑9. 总结带衰减因子的积分器（also known as a Low-pass Filtered Integrator）是在电机控制中对磁链观测器进

数学基础 -- 微积分之三角函数幂的积分

三角函数幂的积分处理 1. 积分形式 1.1 ∫ sin ⁡ m ( x ) cos ⁡ n ( x ) d x \int \sin^m(x) \cos^n(x) \, dx ∫sinm(x)cosn(x)dx 1.1.1 当 n n n 为奇数时分离奇数次幂如果 cos ⁡ n ( x ) \cos^n(x) cosn(x) 是奇数次幂，可以将其分解为 cos ⁡ n −

蒙特卡洛模拟计算圆周率和积分

蒙特卡洛模拟计算圆周率 import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom matplotlib.patches import Circlen = 1000r = 1.0a,b = (0.0,0.0)xmin,xmax = a-r,a+rymin,ymax = b-r,b+rx = np.

绿色积分引领：我店平台的可持续消费革命

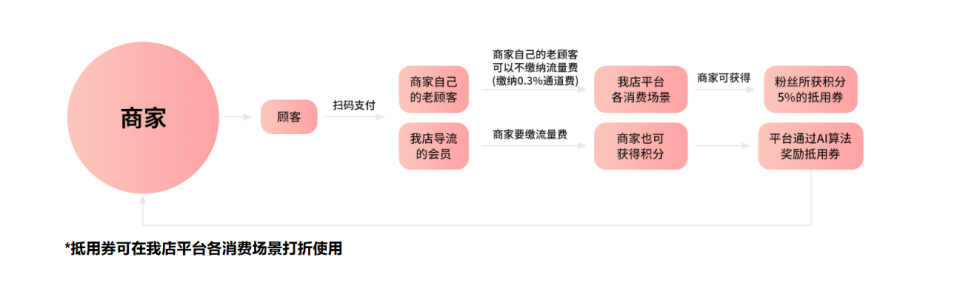
在当今数字化浪潮的推动下，“我店”凭借其创新的环保积分系统，在消费市场中脱颖而出，逐渐改变着市场的结构。本文将详细分析该平台的竞争优势、市场策略以及它如何利用创新手段塑造未来的消费趋势。一、环保积分：消费体验革新的关键自“我店”成立以来，它就致力于打造一个环保且可持续的积分系统，旨在连接消费者与商家。这种模式不仅激发了消费者的购买热情，还吸引了近500万用户注册，并与超过4万家商家

机器视觉中的图像积分图及其实现

https://blog.csdn.net/baimafujinji/article/details/50466224 计算机视觉中，人脸检测（Face Detection）是一项常见的任务。Paul Viola和Michael Jones在《Rapid object detection using a Boosted cascade ofsimple features》一文中提出的快速对

数学基础 -- 积分计算之换元法

换元积分法换元积分法是一种通过变量替换将复杂的积分问题转化为相对简单的积分问题的技巧。该方法的核心思想是通过选取合适的替换变量，将原积分的被积函数形式简化，进而方便计算。换元法的步骤选取替换变量：分析被积函数的形式，选择一个合适的替换变量 u = g ( x ) u = g(x) u=g(x)，使得原积分可以在新的变量下表达为一个较为简单的积分。求导并替换微分：计算所选变量的导

【数值计算方法】蒙特卡洛方法积分的Python实现

原文：https://www.cnblogs.com/aksoam/p/18378332 原理不做赘述,参见【数值计算方法】数值积分&微分-python实现 - FE-有限元鹰 - 博客园,直接上代码,只实现1d,2d积分,N维积分的蒙特卡洛方法也类似. 代码 from typing import Callable,Union,Listdef MonteCarloInt2d(f:Calla

重塑“我店”平台：绿色积分引领的数字消费新纪元

在数字化转型的洪流中，“我店”平台凭借其创新的绿色积分体系异军突起，成为市场中的璀璨新星。本文将深度剖析“我店”的运营模式、市场效应及其如何通过绿色积分机制开创消费新潮流。一、崛起之路与市场震撼力自2021年盛夏在上海启航以来，“我店”平台凭借其独到的商业洞察力和执行力，迅速在业界站稳脚跟。该平台不仅激发了消费者的购物潜能，还成功汇聚了近500万忠实用户，携手4万余家合作商家共创佳

数学基础 -- 定积分的基本思想、定义与性质

定积分的基本思想、定义与性质 1. 定积分的基本思想定积分的基本思想是通过对函数曲线下的面积进行求和，来表示函数在给定区间上的累积效应。具体来说，给定一个函数 f ( x ) f(x) f(x) 和一个区间 [ a , b ] [a, b] [a,b]，定积分可以看作是将该函数在区间 [ a , b ] [a, b] [a,b] 上分成很多小区间，然后求每个小区间上函数值与小区间长度的

数学基础 -- 定积分之估算积分

定积分的估算方法在定积分计算中，常用的估算方法包括矩形法、梯形法、辛普森法和蒙特卡洛方法。 1. 矩形法左矩形法将区间 [ 0 , 1 ] [0, 1] [0,1] 分为4个小区间，长度为 Δ x = 0.25 \Delta x = 0.25 Δx=0.25。左端点为 x 0 = 0 x_0 = 0 x0=0， f ( 0 ) = 0 2 = 0 f(0) = 0^2

基于simulink的PEM燃料电池控制系统建模与仿真,对比PID,积分分离以及滑模控制器

目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 4.1 PID控制器 4.2 积分分离PID控制器 4.3 滑模控制器 5.完整工程文件 1.课题概述基于simulink的PEM燃料电池控制系统建模与仿真,对比PID,积分分离以及滑模控制器。 2.系统仿真结果（完整程序运行后无水印）

超级会员卡积分收银系统源码带完整的安装代码包以及搭建部署教程

系统概述超级会员卡积分收银系统源码是一款专为商业运营打造的综合性软件解决方案。它集成了会员卡管理、积分管理、收银管理等多种功能，旨在为企业提供高效、便捷、准确的运营管理工具。该系统源码采用先进的技术架构，具有良好的稳定性和扩展性，能够适应不同规模和类型的企业需求。它不仅能够提升企业的管理效率，还能够增强客户的消费体验，为企业带来更多的商业价值。代码示例系统特色功能 1.会员卡

多租户积分系统功能清单

全额返现消费新模式，会员裂变模式，积分返利模式

在拆解了近千个商业案例，总结了上百种模式，今天这篇文章我们一起来看一下市面上常用的消费全返模式三种方式，每种方式都有其应用场景和优缺点。第一种，消费返积分这是一种社交电商的经典玩法，通常的形式呢是拼团产品返现，比如购买19块9的产品，一人发起，再找三个人一起拼团，成功以后，平台会将这19块9返给你。注意，返的不是钱，而是积分，积分可以在商城可以兑换商品，通过这个路径能够为商城引

练习题-18 计算两个积分

计算积分 I = ∫ R e − t 4 d t . I=\int_{\mathbb{R}} e^{-t^4} dt. I=∫Re−t4dt. 解：令 x = t 4 x=t^4 x=t4. 则 I = 2 ∫ 0 ∞ e − x ⋅ 1 4 ⋅ x − 3 / 4 d x = 1 2 Γ ( 1 4 ) I = 2\int_0^\infty e^{-x} \cdot \frac{1}{4}\

用微 / 积分思想妙解关于等比数列的和

同理，也是微积分思想：求 (\sum_{k=1}^n q^k) 的和：我们知道几何级数的求和公式： ∑ k = 0 n q k = 1 − q n + 1 1 − q (对于 q ≠ 1 ) \sum_{k=0}^n q^k = \frac{1-q^{n+1}}{1-q} \quad \text{(对于 } q \neq 1\text{)} k=0∑nqk=1−q1−qn+1(