本文主要是介绍MCT Self-Refine:创新集成蒙特卡洛树搜索 (MCTS)提高复杂数学推理任务的性能,超GPT4,使用 LLaMa-3 8B 进行自我优化,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
📜 文献卡
| 题目: Accessing GPT-4 level Mathematical Olympiad Solutions via Monte Carlo Tree Self-refine with LLaMa-3 8B |
|---|
| 作者: Di Zhang; Xiaoshui Huang; Dongzhan Zhou; Yuqiang Li; Wanli Ouyang |
| DOI: 10.48550/arXiv.2406.07394 |
| 摘要: This paper introduces the MCT Self-Refine (MCTSr) algorithm, an innovative integration of Large Language Models (LLMs) with Monte Carlo Tree Search (MCTS), designed to enhance performance in complex mathematical reasoning tasks. Addressing the challenges of accuracy and reliability in LLMs, particularly in strategic and mathematical reasoning, MCTSr leverages systematic exploration and heuristic self-refine mechanisms to improve decision-making frameworks within LLMs. The algorithm constructs a Monte Carlo search tree through iterative processes of Selection, self-refine, self-evaluation, and Backpropagation, utilizing an improved Upper Confidence Bound (UCB) formula to optimize the exploration-exploitation balance. Extensive experiments demonstrate MCTSr’s efficacy in solving Olympiad-level mathematical problems, significantly improving success rates across multiple datasets, including GSM8K, GSM Hard, MATH, and Olympiad-level benchmarks, including Math Odyssey, AIME, and OlympiadBench. The study advances the application of LLMs in complex reasoning tasks and sets a foundation for future AI integration, enhancing decision-making accuracy and reliability in LLM-driven applications. |
| GitHub: 托洛茨基1997/MathBlackBox (github.com) |
⚙️ 内容
本文介绍了一种名为MCTSelf-Refine(MCTSr)的新算法,它将大型语言模型(LLMs)与蒙特卡罗树搜索(MCTS)相结合,旨在提高复杂数学推理任务的表现。该算法通过选择、自我修正、自我评估和反向传播等迭代过程构建一个蒙特卡罗搜索树,并利用改进后的上置信界公式优化探索和开发之间的平衡。实验结果表明,MCTSr在解决奥林匹克级别的数学问题方面非常有效,显著提高了多个数据集的成功率,包括GSM8K、GSM Hard、MATH以及Math Odyssey、AIME和Olympiad-Bench等奥林匹克级别基准测试。这项研究为未来AI集成的应用奠定了基础,增强了基于LLM决策制定的准确性和可靠性。
💡 创新点
- MCT Self-Refine (MCTSr)算法:这是一种创新的集成方式,将LLMs与MCTS相结合,特别设计用于处理复杂的数学推理任务。
- 动态探索与精炼:通过迭代的选择、自我精炼、自我评估和反向传播过程构建蒙特卡洛搜索树,并使用改进的上置信界(UCB)公式来优化探索与利用的平衡。
- 应用范围广泛:实验证明,MCTSr能显著提升在多个数据集上的解题成功率,包括GSM8K、GSM Hard、MATH以及奥林匹克级别的Math Odyssey、AIME和Olympiad-Bench等基准测试。
🧩 不足
尽管MCTSr在数学任务上显示了优势,但其研究仍处于初步阶段,且其潜在应用领域,如黑盒优化和大语言模型的自我驱动校准,需要进一步探索。此外,MCTSr的组件高度可扩展,需要持续开发以识别和比较更广泛的组件算法,以提高实用性和有效性。
🔁 实验卡
💧 数据
实验使用的数据来自多个数据集,包括GSM8K、GSM Hard、MATH,以及奥林匹克数学水平的Math Odyssey、AIME和Olympiad-Bench。这些数据集涵盖了不同难度的数学问题,用以全面测试MCTSr算法的性能。
👩🏻💻 方法
本文提出了一种名为MCTSr(Multi-Criteria Tree Search with Refinement)的对话系统优化算法。该算法主要由初始化、选择、自适应优化、自我评估、反向传播以及UCB更新六个阶段组成。在每个阶段中,算法通过不同的策略和技术来不断优化回答的质量,并探索新的可能性。
首先,在初始化阶段,算法使用一个简单的模型生成的答案和一个“我不知道”的占位符答案来建立根节点,以减少过拟合的风险。然后,在选择阶段,算法利用价值函数Q对未完全展开的所有答案进行排名,并根据贪婪策略选择最高价值的节点进行进一步的探索和细化。接着,在自适应优化阶段,算法使用多轮对话反馈引导模型对选定的回答进行优化,从而产生更优的回答a’。在自我评估阶段,算法对优化后的回答进行评分,计算其奖励值和Q值,并引入严格的评分标准和抑制完美分数等约束条件,以确保评分的可靠性和公平性。在反向传播阶段,算法将优化后回答的价值信息向前传递到父节点和其他相关节点,如果任何子节点的Q值发生变化,则更新父节点的Q值。最后,在UCB更新阶段,算法使用UCB公式更新所有节点的UCB值,以便在下一个选择阶段中识别出候选节点并进行进一步扩展或选择。
总结:
- MCTS与LLMs集成:通过集成MCTS到LLMs中,利用MCTS的四阶段流程(选择、扩展、模拟和反向传播)来逐步构建决策树,并通过LLMs提供问题解答。
- 动态剪枝策略:采用改进的UCB公式动态调整探索与利用的平衡,提高了搜索效率和精确度。
- 自我精炼与自我奖励评估:MCTSr引入了机制,允许模型通过迭代过程自我精炼其响应,并通过自我奖励机制评价,这是之前方法所缺乏的。
方法改进:
与传统的基于深度强化学习的对话系统优化算法相比,MCTSr具有以下优点:
- 多目标优化:MCTSr考虑了多个评价指标,如准确性、流畅度、多样性等,使得对话系统的回答更加全面和优质。
- 自我评估机制:MCTSr引入了自我评估机制,通过对回答进行评分并计算奖励值和Q值,可以有效降低过拟合风险,提高回答质量。
- 反向传播技术:MCTSr采用了反向传播技术,将优化后回答的价值信息向前传递到父节点和其他相关节点,可以更好地维护树结构的信息。
🔬 实验
本文主要介绍了MCT Sr算法在解决数学问题方面的应用,并进行了多组对比实验来验证其效果。具体来说,文章包括以下四个部分:
第一部分是MCT Sr算法的原理和实现细节,主要包括自评价、回溯更新和选择策略等三个步骤。
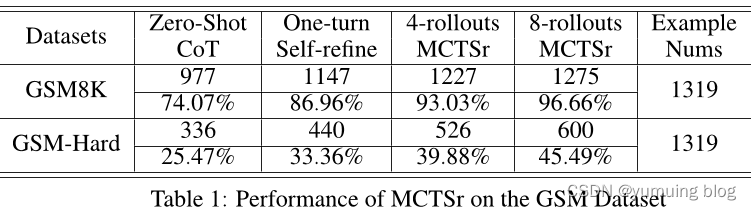
第二部分是对MCT Sr算法的效果进行了评估,通过与GPT-4、Claude 3和Gemini 1.5-Pro等当前最新的封闭源模型进行比较,在多个数据集上测试了算法的表现。其中,实验结果表明随着rollout数的增加,算法的成功率也显著提高,尤其是在较简单的GSM8K数据集中表现更好。然而,在更复杂的GSM-Hard数据集中,算法的性能存在一定的局限性。
第三部分是在MATH数据集上的实验,通过对不同难度级别的问题进行测试,进一步验证了MCT Sr算法的有效性。结果显示,随着rollout数的增加,算法在各个难度级别上的成功率都有所提高,特别是在最困难的第五级中,算法仍然能够取得相对较高的成功率。
第四部分是在奥林匹克竞赛级别的数据集上的实验,包括AIME、GAIC Math Odyssey和OlympiadBench等数据集。结果显示,随着rollout数的增加,算法在这些数据集上的成功率也有明显提高,特别是在GAIC Math Odyssey数据集上,算法的性能得到了更好的展示。
📜 结论
MCTSr算法成功增强了LLMs解决复杂数学问题的能力,为未来AI技术的融合以提高决策和推理准确性奠定了基础。然而,其在更广泛场景下的应用,比如黑盒优化,仍有待进一步研究。
总的来说,本文对MCT Sr算法在解决数学问题方面的应用进行了全面的评估和分析,证明了该算法的有效性和实用性。

🤔 总结卡
文章优点
该研究提出了一种新的算法——MCT Self-Refine(MCTSr),将蒙特卡罗树搜索(MCTS)与大型语言模型相结合,以提高数学问题解决的能力。实验结果表明,在多个数据集上显著提高了解决问题的成功率,并在奥林匹克级别的数学挑战中表现出色。此外,该研究为未来进一步探索MCTSr在更广泛场景中的应用提供了基础。
方法创新点
该研究通过结合MCTS和LLMs的优点,解决了LLMs在精确性和可靠性方面的问题。同时,他们还开发了动态剪枝模块来优化决策过程,使问题求解更加高效和准确。这种方法的创新在于它成功地将两个不同的领域进行了整合,从而提高了LMMs在复杂推理任务上的性能。
未来展望
尽管MCT Sr已经证明了其在数学问题解决方面的潜力,但其在其他领域的应用仍需进一步探索,如黑盒优化和自我驱动的对齐。未来的研究将继续优化算法组件并测试它们在各种问题和环境下的表现,以实现更广泛的实用性和有效性。此外,这项研究为进一步整合AI技术以增强决策和推理准确性奠定了基础。
这篇关于MCT Self-Refine:创新集成蒙特卡洛树搜索 (MCTS)提高复杂数学推理任务的性能,超GPT4,使用 LLaMa-3 8B 进行自我优化的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




