本文主要是介绍蒙特卡洛光线追踪 蒙特卡洛积分 基础知识三,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
蒙特卡洛光线追踪技术系列 见 蒙特卡洛光线追踪技术
多维蒙特卡罗积分
将前面的等式应用于多维积分是很简单的,除了选择多维采样点可能比一维情况更复杂。作为二维中的一个例子,假设我们想在原点中心的正方形 [-1,1]^2 上积分一些函数 f 。这可以记为单个二维变量x上的积分:
![]()
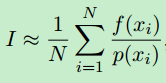
在每个 xi 是二维点分布的二维密度P。我们可以转换成更明确的笛卡尔坐标,并且有一种形式,我们可能更舒服:
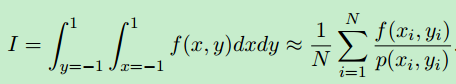
这与上面的形式没有什么不同,除了我们看到席的显式成分是(xi,yi)。
如果我们的积分超过半径R,没有什么变化,除了采样点必须按照圆盘上的密度分布。这就是蒙特卡罗积分相对容易的原因:一旦选择了样本点,公式的应用总是一样的。
翻译了这么多,我们现在把之前的部分再解释记录一下,为了确保真正理解蒙特卡洛积分的原理。
首先,假设有一个正方形,简单起见我们先说第一种情况:正方形上每个点出现的概率都是一样的,总概率为1。但是每个点的值不一定一样。现在我们要求这个正方形所有点的平均值(可以理解为一个正方形区域的平均海拔)。
 (图片来自网络,侵删)
(图片来自网络,侵删)
则我们随机从正方形图上抽取一些点,然后取平均,抽取的点数越多,平均值越接近于平均海拔。
现在有意思的要来了:正方形上每个点出现的概率不一定一样,但是总概率的和为1。比如,中间出现的概率第一些,两边出现的概率高一些,大概是盆地形状(区分开每个点出现的概率和该点的值,是不一样的)。、
现在我们要想求该区域的值,就应该采用重要性抽样,即出现概率低的地方采样少一点,出现概率高的地方采样多一点。
所以如果正方形上每个点出现概率不一样的话,我们就不能仅仅只依靠这个采样函数了:

因为最后面的式子只给出了要采样的点的值,但是没有告诉概率因素。
这篇关于蒙特卡洛光线追踪 蒙特卡洛积分 基础知识三的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






