本文主要是介绍用于时间序列概率预测的蒙特卡洛模拟,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
大家好,蒙特卡洛模拟是一种广泛应用于各个领域的计算技术,它通过从概率分布中随机抽取大量样本,并对结果进行统计分析,从而模拟复杂系统的行为。这种技术具有很强的适用性,在金融建模、工程设计、物理模拟、运筹优化以及风险管理等领域都有广泛的应用。
蒙特卡洛模拟这个名称源自于摩纳哥王国的蒙特卡洛城市,这里曾经是世界著名的赌博天堂。在20世纪40年代,著名科学家乌拉姆和冯·诺依曼参与了曼哈顿计划,他们需要解决与核反应堆中子行为相关的复杂数学问题。他们受到了赌场中掷骰子的启发,设想用随机数来模拟中子在反应堆中的扩散过程,并将这种基于随机抽样的计算方法命名为"蒙特卡洛模拟"(Monte Carlo simulation)。
蒙特卡洛模拟的核心思想是通过大量重复随机试验,从而近似求解分析解难以获得的复杂问题。它克服了传统数值计算方法的局限性,能够处理非线性、高维、随机等复杂情况。随着计算机性能的飞速发展,蒙特卡洛模拟的应用范围也在不断扩展。
在金融领域,蒙特卡洛模拟被广泛用于定价衍生品、管理投资组合风险、预测市场波动等。在工程设计中,它可以模拟材料力学性能、流体动力学等复杂物理过程。在物理学研究中,从粒子物理到天体物理,都可以借助蒙特卡洛模拟进行探索。此外,蒙特卡洛模拟还在机器学习、计算生物学、运筹优化等领域发挥着重要作用。
蒙特卡洛模拟的过程基本上是这样的:首先需要定义要模拟的系统或过程,包括方程和参数;其次根据拟合的概率分布生成随机样本;进而针对每一组随机样本,运行模型模拟系统的行为;最后分析结果以了解系统行为。
本文将介绍使用它来模拟未来证券价格的两种分布:高斯分布和学生 t 分布。这两种分布通常被量化分析人员用于证券市场数据。
在此加载苹果公司从2020年到2024年每日证券价格的数据:
import yfinance as yf
orig = yf.download(["AAPL"], start="2020-01-01", end="2024-12-31")
orig = orig[('Adj Close')]
orig.tail()
[*********************100%%**********************] 1 of 1 completed
Date
2024-03-08 170.729996
2024-03-11 172.750000
2024-03-12 173.229996
2024-03-13 171.130005
2024-03-14 173.000000
Name: Adj Close, dtype: float64
可以通过价格序列来计算简单的日收益率,并将其呈现为柱状图。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
returns = orig.pct_change()
last_price = orig[-1]
returns.hist(bins=100)
苹果证券日收益柱状图
1.标准正态分布拟合收益率
证券的历史波动率通常是通过计算每日收益率的标准差来进行,假设未来的波动率与历史波动率相似。而直方图则呈现了以0.0为中心的正态分布的形状。为简单起见,将该分布假定为均值为0,标准差为0的高斯分布。接下来计算出标准差(也称为日波动率),预计明天的日收益率将会是高斯分布中的一个随机值。
daily_volatility = returns.std()
rtn = np.random.normal(0, daily_volatility)
第二天的价格是今天的价格乘以 (1+return %):
price = last_price * (1 + rtn)
以上是证券价格和收益的基本财务公式。使用蒙特卡洛模拟预测明天的价格,可以随机抽取另一个收益率,从而推算后天的价格,可以得出未来 200 天可能的价格走势之一。当然,这只是一种可能的价格路径。重复这个过程得出另一条价格路径,重复过程 1,000 次,得出 1,000 条价格路径。
import warnings
warnings.simplefilter(action='ignore', category=pd.errors.PerformanceWarning)num_simulations = 1000
num_days = 200
simulation_df = pd.DataFrame()
for x in range(num_simulations):count = 0 # The first price pointprice_series = []rtn = np.random.normal(0, daily_volatility)price = last_price * (1 + rtn)price_series.append(price)# Create each price pathfor g in range(num_days):rtn = np.random.normal(0, daily_volatility)price = price_series[g] * (1 + rtn)price_series.append(price)# Save all the possible price pathssimulation_df[x] = price_series
fig = plt.figure()
plt.plot(simulation_df)
plt.xlabel('Number of days')
plt.ylabel('Possible prices')
plt.axhline(y = last_price, color = 'b', linestyle = '-')
plt.show()
分析结果如下:价格起始于179.66美元,大部分价格路径相互交叠,模拟价格范围为100美元至500美元。
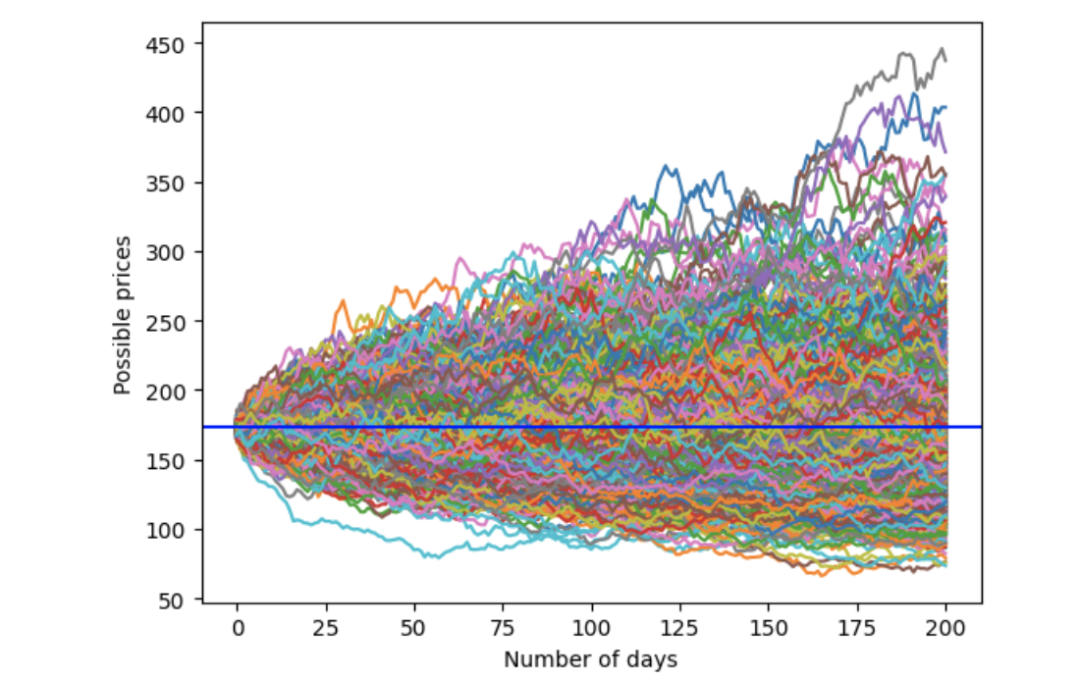
使用高斯分布的蒙特卡洛模拟
假设我们想知道90%情况下(5%到95%)出现的"正常"价格范围,可以使用量化方法得到上限和下限,从而评估超出这些极端价格。
upper = simulation_df.quantile(.95, axis=1)
lower = simulation_df.quantile(.05, axis=1)
stock_range = pd.concat([upper, lower], axis=1)fig = plt.figure()
plt.plot(stock_range)
plt.xlabel('Number of days')
plt.ylabel('Possible prices')
plt.axhline(y = last_price, color = 'b', linestyle = '-')
plt.show()
使用高斯分布的 95 百分位数和 5 百分位数
2.学生t分布拟合收益率
证券价格回报偶尔会出现极端事件,位于分布两端。标准正态分布预计 95% 的收益率发生在两个标准差之内,5% 的收益率发生在两个标准差之外。如果极端事件发生的频率超过 5%,分布看起来就会 "变胖"。这就是统计学家所说的肥尾,定量分析人员通常使用学生 t 分布来模拟证券收益率。
学生 t 分布有三个参数:自由度参数、标度和位置。
-
自由度:自由度参数表示用于估计群体参数的样本中独立观测值的数量。自由度越大,t 分布的形状越接近标准正态分布。在 t 分布中,自由度范围是大于 0 的任何正实数。
-
标度:标度参数代表分布的扩散性或变异性,通常是采样群体的标准差。
-
位置:位置参数表示分布的位置或中心,即采样群体的平均值。当自由度较小时,t 分布的尾部较重,类似于胖尾分布。
用学生 t 分布来拟合实际证券收益率:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import treturns = orig.pct_change()# Number of samples per simulation
num_samples = 100# distribution fitting
returns = returns[1::] # Drop the first element, which is "NA"
params = t.fit(returns[1::]) # fit with a student-t# Generate random numbers from Student's t-distribution
results = t.rvs(df=params[0], loc=params[1], scale=params[2], size=1000)
# Generate random numbers from Student's t-distribution
results = t.rvs(df=params[0], loc=params[1], scale=params[2], size=1000)
print('degree of freedom = ', params[0])
print('loc = ', params[1])
print('scale = ', params[2])
参数如下:
-
自由度 = 3.735
-
位置 = 0.001
-
标度 = 0.014
使用这些参数来预测 Student-t 分布,然后用 Student-t 分布绘制实际证券收益分布图。
returns.hist(bins=100,density=True, alpha=0.6, color='b', label='Actual returns distribution')# Plot histogram of results
plt.hist(results, bins=100, density=True, alpha=0.6, color='g', label='Simulated Student/t distribution')plt.xlabel('Value')
plt.ylabel('Density')
plt.title('Actual returns vs. Projections with a Student\'s t-distribution')
plt.legend(loc='center left')
plt.grid(True)
plt.show()
实际回报与预测相当接近:
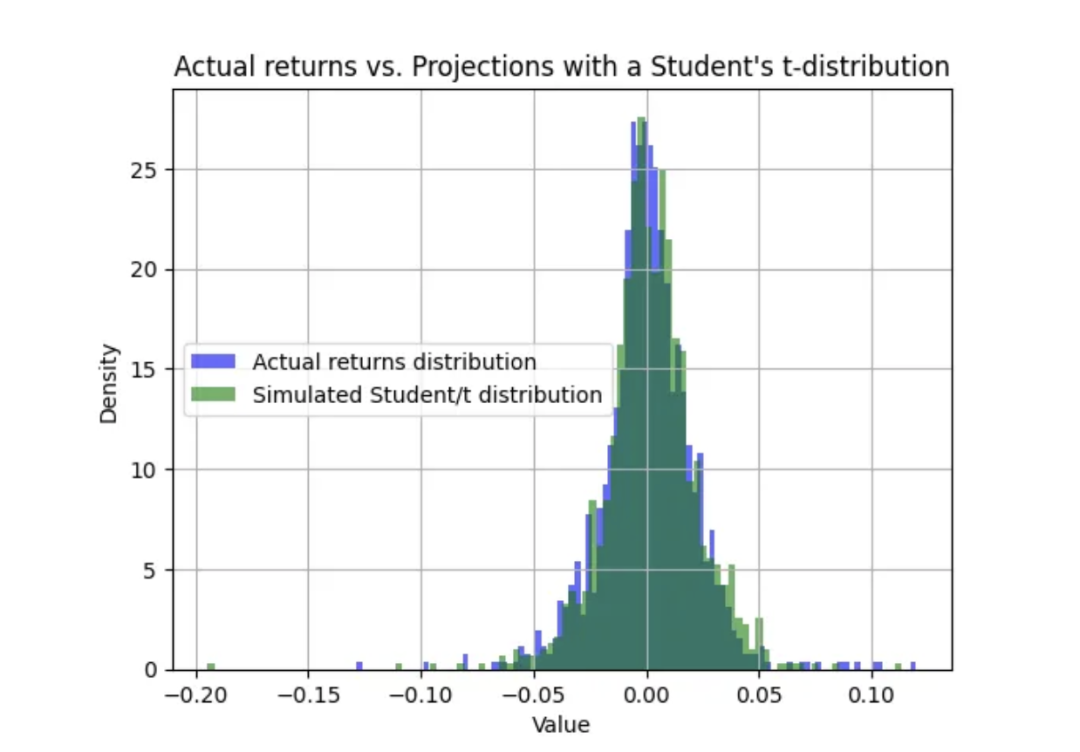
实际收益与学生 t 分布预测对比
与之前一样,模拟未来 200 天的价格走势。
import warnings
warnings.simplefilter(action='ignore', category=pd.errors.PerformanceWarning)num_simulations = 1000
num_days = 200
simulation_student_t = pd.DataFrame()
for x in range(num_simulations):count = 0# The first price pointprice_series = []rtn = t.rvs(df=params[0], loc=params[1], scale=params[2], size=1)[0]price = last_price * (1 + rtn)price_series.append(price)# Create each price pathfor g in range(num_days):rtn = t.rvs(df=params[0], loc=params[1], scale=params[2], size=1)[0]price = price_series[g] * (1 + rtn)price_series.append(price)# Save all the possible price pathssimulation_student_t[x] = price_series
fig = plt.figure()
plt.plot(simulation_student_t)
plt.xlabel('Number of days')
plt.ylabel('Possible prices')
plt.axhline(y = last_price, color = 'b', linestyle = '-')
plt.show()
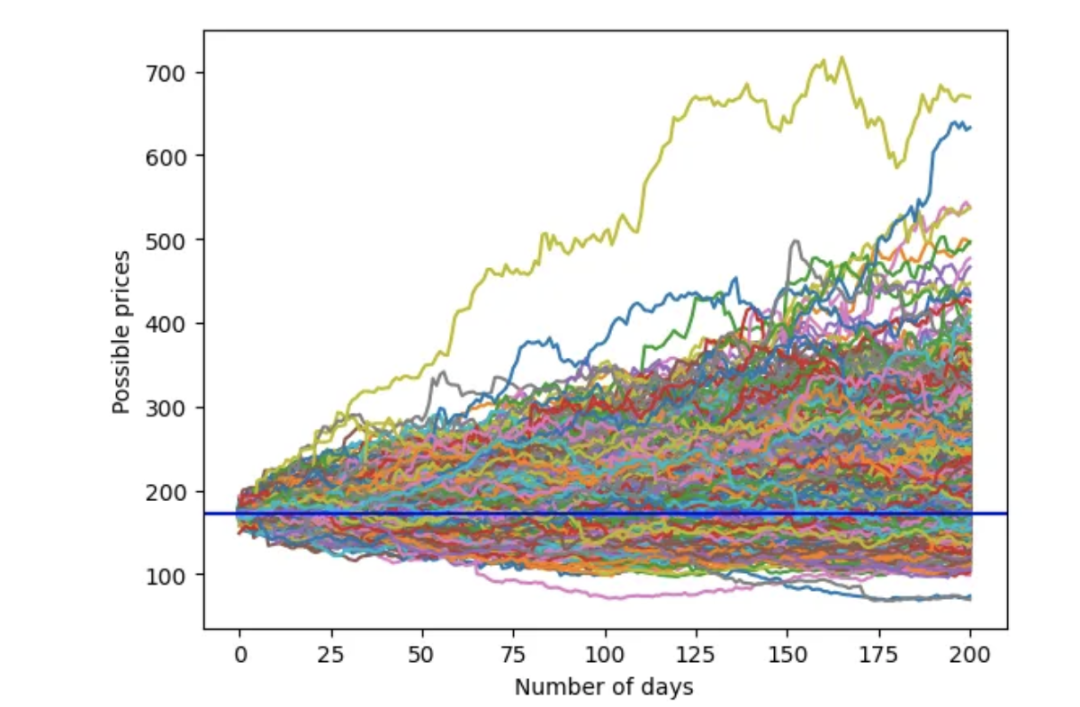
学生 t 分布的蒙特卡洛模拟
可以绘制出学生 t 的蒙特卡洛模拟置信区间上下限(95%、5%):
upper = simulation_student_t.quantile(.95, axis=1)
lower = simulation_student_t.quantile(.05, axis=1)
stock_range = pd.concat([upper, lower], axis=1)fig = plt.figure()
plt.plot(stock_range)
plt.xlabel('Number of days')
plt.ylabel('Possible prices')
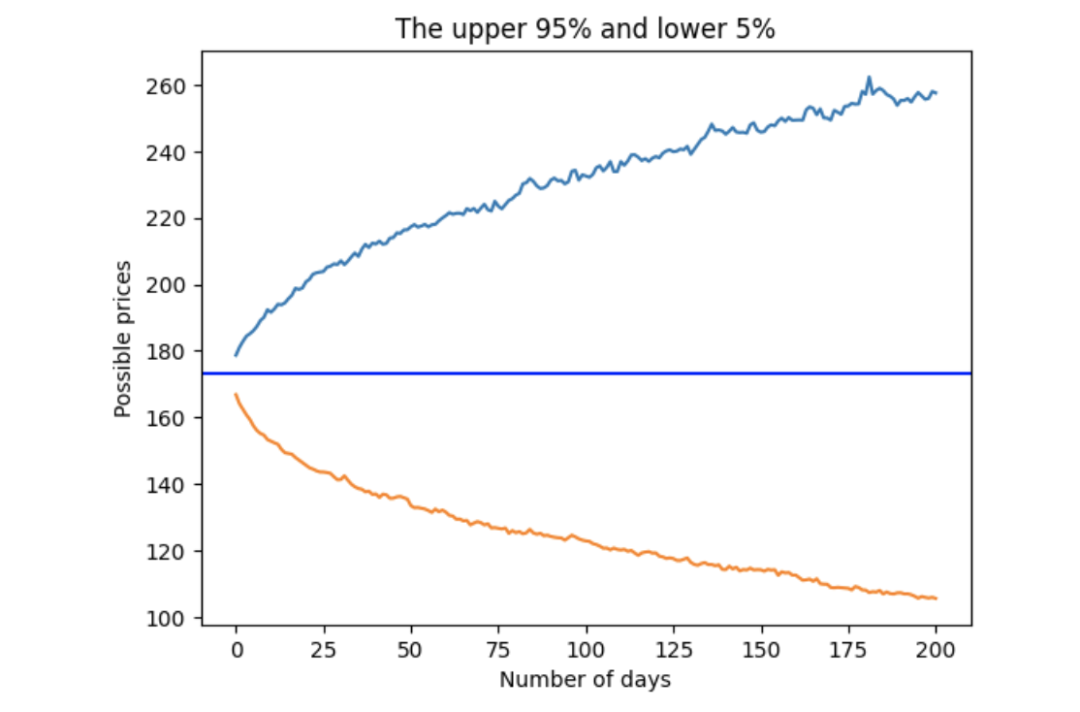
plt.title('The upper 95% and lower 5%')
plt.axhline(y = last_price, color = 'b', linestyle = '-')
plt.show()
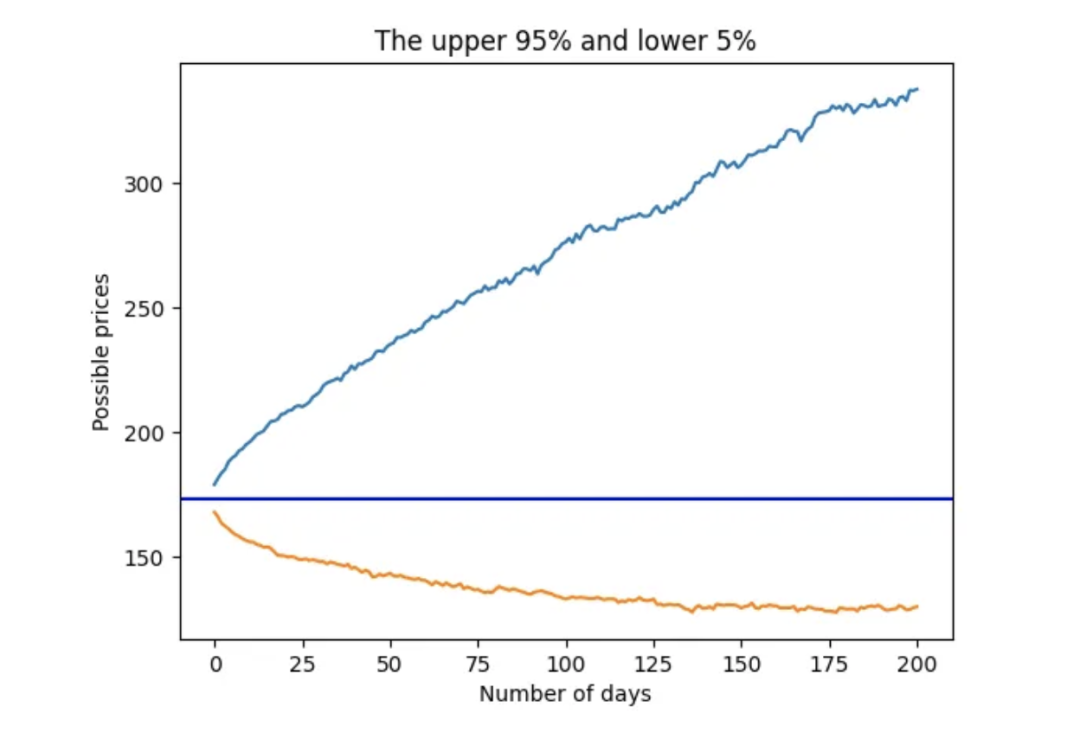
使用学生 t 分布的 95 百分位数和 5 百分位数
这篇关于用于时间序列概率预测的蒙特卡洛模拟的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





