省选专题

2024省选复习计划

NOIP 时间：2024.11.30 距离 NOIP 还有 101 天省选时间：2025.4.1（预计时间）距离省选还有 223 天阶段一：数据结构练习标签说明：（^）我没学过的，（-min）用的比较少，以后再学的。动态规划基础dp P5662 [CSP-J2019] 纪念品 P1156 垃圾陷阱 P5020 [NOIP2018 提高组] 货币系统区间dp P188

2021统一省选 A卷 day1解析

题面，就参照洛谷的吧。卡牌游戏矩阵游戏图函数重点看思维过程。卡牌游戏爆搜的话，过前两个点没问题。枚举要翻牌的数量m，然后从n张中翻m张，直接统计最大最小值。考虑到卡牌是按照正面数值由小到大排序的，设c[]数组，将a[]和b[]存入c[]，然后由小到大排序。枚举最小值minn为c[i]，最大值maxn为c[j]，这两个值是不可更改的，现在转为判定性问题，注意minn和maxn不

Day1 省选衔接题思路总结

Day1 省选题思路取数可反悔的贪心。我们开一个双向链表记录此时每个数的前/后一个数是什么。一个简单但不一定正确的贪心策略即为：每次都取走当前值最大的且可取的数，并更新列表。考虑如何使这个贪心思路正确。设 p r e x pre_x prex 表示 x x x 的前一个元素， n x t x nxt_x nxtx 表示 x x x 的后一个元素， w ( x ) w(

省选模拟赛20200229（by Ark） T3 买买买（动态点分治）

题解 ٩(๑>◡<๑)۶人生第一道动态点分治٩(๑>◡<๑)۶ 一开始我点分治都不怎么会，更别说动态点分治了然后开始肝题解和std，肝了我两天，终于搞懂了然后写了一上午+下午，调了一晚上，终于A掉了如果不知道动态点分治，请看这里其实这道题思路并不难想点分树+线段树只是修改边的时候会比较麻烦考虑一条边改变权值会对哪些点产生影响，其

jzoj5765 【省选模拟8.5】相互再归的鹅妈妈（集合划分，斯特林反演）

mk<=5e6，m<=5e4 m k <= 5 e 6 ， m <= 5 e 4 mk<=5e6，m<=5e4 解法先考虑可以有相同怎么做：枚举一个第一个脱离限制的位置，然后用一个脱离限制的数来安排使得异或和为0，其他数可以任意取（要分是否脱离限制确定方案数）。这样可以计算出g(n)表示n个可以相同的数，异或和为0的答案。斯特林反演式子： [n=1]=∑m的集合划分A

2020省选A卷组合数问题

求 ∑ k = 0 n f ( k ) x k ( n k ) \sum_{k=0}^{n} f(k) x^{k} \binom{n}{k} k=0∑nf(k)xk(kn) n ≤ 1000 \ n \le 1000 n≤1000， m ≤ 1000 \ m \le 1000 m≤1000 求杨辉三角，枚举即可。 m = 0 \ m=0 m=0 根据二项式定理，即 a

省选 2017 杂题汇总

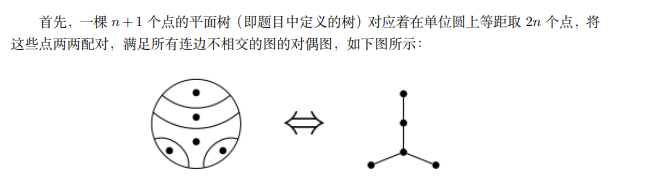
[ZJOI2017]仙人掌发现可以把一个仙人掌看做所有环组成的图，如果不是环而是单个边，我们可以手动给它填一条边变成环考虑一棵树怎么做？就是在树上选若干条互不相交的链的方案数，考虑树形 d p dp dp f i f_{i} fi 表示到 i 的子树的方案数， g i g_i gi 表示一个点有 i 条边相连，两两配对或者单身的方案数 g i = g i − 1 + ( i − 1

省选 2018 杂题汇总

由于这些省太强了，6道做完不现实，于是就选了一些简单的做 [SDOI2018]战略游戏答案为两条路径的必经的割点，正好是两点在圆方树上的圆点个数然后每次询问建立虚树查询一下即可 [SDOI2018]荣誉称号题意：将所有二叉树上含有 k+1 个点的路径的 ∑ a i \sum a_i ∑ai 变成 m 的倍数的最小代价发现一个点与它的 k+1 级祖先同余，也就是说我们只需要考虑 k+1

省选模拟 19/10/15

T1 开始是这么写的，修改父亲的时候，改 E [ A [ i ] ] E[A[i]] E[A[i]]，然后改 A [ i ] A[i] A[i] 一圈的 C [ i ] C[i] C[i] 然后这样最坏是 O ( n ) O(n) O(n) 的令 G [ i ] = B [ i ] − E [ i ] ∗ D [ i ] + E [ i ] G[i]=B[i]-E[i]*D[i]+E[

【省选模拟】Fac （生成函数）（组合意义）（拉格朗日反演）（倍增）（多项式全家桶）

传送门没有题解是真的秀，连蒙带猜搞了一天结果今天早上才写完，不过还好有 3 个神仙学长助力不知道题解是怎么想到的，所以只好直接说结论了经观察发现可以先求出 ( i k i − 1 ) 1 i \binom{ik}{i-1}\frac{1}{i} (i−1ik)i1，这个在 k = 2 k=2 k=2 的时候是卡特兰数也就是二叉树的个数考虑将其扩展为 k k k 叉树，即证

【省选模拟】20/03/21 （「USACO 2020.1 Platinum」）

C a v e P a i n t i n g s Cave Paintings CavePaintings 考虑一层与上面一层的连边，最后会连成一个森林，一个点选了它的子树必须都选，于是做一遍树形 d p dp dp 就可以了，建边可以用并查集模拟 C o d e Code Code N o n − D e c r e a s i n g S u b s e q u e n c e

【省选模拟】complex（启发式分裂）

3.14 3.14 3.14题解：如果一个大区间不合法那么必存在一种颜色使得它在这个区间的出现次数 < b [ l e n ] <b[len] <b[len]，注意到 l e n len len 缩短 b [ l e n ] b[len] b[len] 将增大，于是我们选出的子区间必定不包含这种颜色这种颜色会将区间分成若干段，但是没必要分裂完，我们找到左右第一个不满足的颜色往下分，复杂

【省选模拟】Comet OJ - Contest #16 小 C 的奇妙序列（DP）（组合意义）（拆分数）

传送门先说一下 k = 2 k=2 k=2怎么做，要求 E ( a i 2 ) = E ( ∑ ( a i + a j ) 2 ) = 2 ∑ E ( a i 2 ) + 2 ( ∑ a i ) 2 E(a_i^2)=E(\sum (a_i+a_j)^2)=2\sum E(a_i^2)+2(\sum a_i)^2 E(ai2)=E(∑(ai+aj)2)=2∑E(ai2)+2(∑a

【省选模拟】20/06/08

A A A 考虑容斥，1表示钦定选，0 的位置表示 0/1 均合法，这样的好处是可以只考虑 1 的限制并且最后我们只需对超集容斥就可以得到答案发现钦定一些 1 选的意义就是在原图上选若干条不相交的链，复杂度和拆分数有关预处理一个集合有多少条链，那么就是一个子集卷积并且发现只用求出最后一项，所以可以 O ( 2 n ) O(2^n) O(2n) 暴力容斥回去复杂度 O ( n 2

【省选模拟】20/06/05

A A A l d x ldx ldx 大神的 60 60 60 分做法：用二元组 ( a , b ) (a,b) (a,b) 记录最小段数和最小代价来 d p dp dp，记 d p i dp_i dpi 表示以 i i i 结尾的最小值考虑如何为一个区间选择一个最优的匹配点，暴力枚举 d p j dp_j dpj，考虑将某一个区间从 j j j 挪到 i i i

【省选模拟】20/06/03

Pro Sol 考场疯狂 r u s h rush rush 两份 5 k 5k 5k 的代码，死掉了。。。 A A A：直接小常数 n 3 n^3 n3 d p dp dp 可以拿 70 考虑可反悔贪心，一个不是最优的策略是每次将这一位加 2，将下一位加 1 考虑反悔，用最快的策略将当前位填满，并且只需要考虑反悔 i − 1 i-1 i−1 的决策对于 ( i − 1 ,

【省选模拟】20/06/02

A A A 发现只需要压黑白开头存不存在为偶数的，若存在，其他偶数边随便选不选这条边的选发是唯一的， d p dp dp 即可， C o d e Code Code B B B 补集转换一下，枚举两个不交的集合，考虑他们向外的连边，强制指向这个集合对于选定的集合，要统计其联通的方案数，容斥 d p dp dp 即可， C o d e Code Code C C C 性质：最后选

【省选模拟】20/05/31

Sol A A A 考虑每个位置有个被最早染黑的时间，求的就是这些时间的第 k k k 大 m i n m a x minmax minmax 容斥一下，就是求 ∑ T ≠ ∅ ( ∣ T ∣ − 1 k − 1 ) ( − 1 ) ∣ T ∣ − k ( n + 1 2 ) ( n + 1 2 ) − c o e f ( T ) \sum_{T\neq \empty}\binom{

【省选模拟】20/05/29

A A A 从父亲继承线性基，每一位保留深度最大的点， C o d e Code Code B B B 考虑二分这个 k k k，我们暴力建出图，用 h a s h hash hash 来判重和连边，合法当且仅当没有环，考虑怎么输出方案，首先可以在 d a g dag dag 贪心出每个点向后的最长链，只需要考虑起点，发现需要支持比较两个串的字典序，选好起点之后在 d a g d

【省选模拟】20/05/26

A A A 考虑限制为 [ l , r ] [l,r] [l,r] 中没有值出现两次， m a x i ∈ [ l , r ] a i = l e n max_{i\in [l,r]} a_i=len maxi∈[l,r]ai=len， m i n i ∈ [ l , r ] a i = 1 min_{i\in [l,r]}a_i=1 mini∈[l,r]ai=1，对每个右端点统计，

【2022省选模拟】喜欢最最痛——数据结构、凸包、二分

我找不到原题链接题目描述题解答案可以分为两部分：树上的原边、额外边。假设我们要用 i i i 条额外边，那么一定是选当前可选的最短的 i i i 条边，所以选的额外边的权值和一定是关于 i i i 单增的下凸包。对于树上的原边，如果不加额外边那么代价一定是 2 ∗ 边权和 2*边权和 2∗边权和。加一条额外边时，正好可以让树上少走一条简单路径，我们要最小化代价，即

JZOJ6675. 【2020.05.30省选模拟】交通网络

Description n < = 5 e 5 n<=5e5 n<=5e5 Solution O(n^4) 直接放弃思考矩阵树即可过 n < = 80 n<=80 n<=80，获得23分。 O(n^2) 考虑先枚举一些特殊边，将n个点分成m个联通块，再用prufer序列计算这个完全图的方案数： n m − 2 ∏ i = 1 m s i n^{m-2}\prod_{i=1}^ms

[省选联考 2020 B 卷] 卡牌游戏

目录题目描述输入输出样例输入数据 1 输出数据 1 输入数据 2 输出数据 2 提示分析 Code 题目描述轩轩某天想到了一个卡牌游戏，游戏规则如下：初始时轩轩的手中有自左向右排成一排的 nn 张卡牌，每张卡牌上有一个整数分值。接下来，轩轩每次可以选取卡牌序列最左边的连续若干张卡牌（至少 22 张），将它们替换为一张新卡牌。新卡牌将插入到序列的最

#（树形动规）洛谷P3174 [HAOI2009]毛毛虫（省选/NOi-）

题目描述对于一棵树，我们可以将某条链和与该链相连的边抽出来，看上去就象成一个毛毛虫，点数越多，毛毛虫就越大。例如下图左边的树（图 1 ）抽出一部分就变成了右边的一个毛毛虫了（图 2 ）。输入格式在文本文件 worm.in 中第一行两个整数 N ， M ，分别表示树中结点个数和树的边数。接下来 M 行，每行两个整数 a, b 表示点 a 和点 b 有边连接（ a, b ≤ N ）。

JZOJ 5833. 【省选模拟8.20】Endless Fantasy

中二少年cenbo幻想自己统治着Euphoric Field。由此他开始了Endless Fantasy。 Euphoric Field有n座城市，m个民族。这些城市之间由n-1条道路连接形成了以城市1为根的有根树。每个城市都是某一民族的聚居地，cenbo知道第i个城市的民族是A_i，人数是B_i。为了维护稳定，cenbo需要知道某个区域内人数最多的民族。他向你提出n个询问，其中第i个询