#（树形动规）洛谷P3174 [HAOI2009]毛毛虫（省选/NOi-）

本文主要是介绍#（树形动规）洛谷P3174 [HAOI2009]毛毛虫（省选/NOi-），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

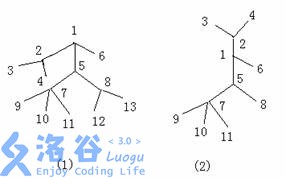
对于一棵树，我们可以将某条链和与该链相连的边抽出来，看上去就象成一个毛毛虫，点数越多，毛毛虫就越大。例如下图左边的树（图 1 ）抽出一部分就变成了右边的一个毛毛虫了（图 2 ）。

输入格式

在文本文件 worm.in 中第一行两个整数 N ， M ，分别表示树中结点个数和树的边数。

接下来 M 行，每行两个整数 a, b 表示点 a 和点 b 有边连接（ a, b ≤ N ）。你可以假定没有一对相同的 (a, b) 会出现一次以上。

输出格式

在文本文件 worm.out 中写入一个整数 , 表示最大的毛毛虫的大小。

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

40% 的数据， N ≤ 50000

100% 的数据， N ≤ 300000

问题分析：

等价于给你一棵树，找出树上的一条链，满足该链长度和该链上子链的数目之和最大！

设f[i][j]表示从i节点到j节点的最大子链数目，对于任意节点f[i][i]=c[i],c数组存储i节点的度

对于节点i和它的儿子：f[i][ai]=c[i]+c[ai]-1;

对于节点i,j链上的任意点k,f[i][j]=f[i][k]+f[k][j]-sz[k];

树形DP？我太菜了不会怎么办qwq

~~先推一波式子~~

令点权 $\sum a[i]∑a[i] （?）$

然后我们发现，每条在该链中的边被多算了一次，设

因为答案求的是点，所以还要再

所以~~真正的~~答案就是 $\sum a[i]-(s-1)+1∑a[i]−(s−1)+1$

emm....好像还是有点麻烦，~~再化化式子~~

$\sum a[i]-(s-1)+1 == \sum a[i]-s+2 == \sum(a[i]-1)+2∑a[i]−(s−1)+1==∑a[i]−s+2==∑(a[i]−1)+2$

根据这个式子，我们把点权全部 $\sum(a[i]-1)∑(a[i]−1) 就是选定的链的长度$

然后~~愉快的~~跑两遍

代码：

#include<bits/stdc++.h>
struct E{int u,nxt;}e[600001];
int p[300001],a[300001],num,mx;
inline void add(int x,int y){e[++num]=(E){y,p[x]},p[x]=num;}
inline void dfs(int fa,int s,int dis){
if(dis>mx) mx=dis,num=s;
for(int i=p[s];i;i=e[i].nxt) if(e[i].u!=fa) dfs(s,e[i].u,dis+a[s]);
}
int main(){
int n,m,x,y;
scanf("%d%d",&n,&m),memset(a,-1,sizeof(a));
for(int i=1;i<n;i++) scanf("%d%d",&x,&y),add(x,y),add(y,x),a[x]++,a[y]++;
dfs(0,1,a[1]),mx=0,dfs(0,num,a[num]),printf("%d",mx+2);
return 0;
}