本文主要是介绍【省选模拟】20/05/31,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Sol
A A A
-
考虑每个位置有个被最早染黑的时间,求的就是这些时间的第 k k k 大
m i n m a x minmax minmax 容斥一下,就是求
∑ T ≠ ∅ ( ∣ T ∣ − 1 k − 1 ) ( − 1 ) ∣ T ∣ − k ( n + 1 2 ) ( n + 1 2 ) − c o e f ( T ) \sum_{T\neq \empty}\binom{|T|-1}{k-1}(-1)^{|T|-k}\frac{\binom{n+1}{2}}{\binom{n+1}{2}-coef(T)} T=∅∑(k−1∣T∣−1)(−1)∣T∣−k(2n+1)−coef(T)(2n+1)
其中 c o e f coef coef 是不包含集合 T T T 的区间个数,考虑 d p i , j , k dp_{i,j,k} dpi,j,k 表示当前选到 i i i, ∣ T ∣ = j |T|=j ∣T∣=j, c o e f ( T ) = k coef(T)=k coef(T)=k 的方案数,状态很少 O ( n 5 ) O(n^5) O(n5) 可以通过 -
考虑一个复杂度更好看但肯定跑不过 n 5 n^5 n5 的做法,我们先把转移写出来
d p i , j , k = ∑ l < i d p l , j − 1 , k − ( i − l 2 ) dp_{i,j,k}=\sum_{l<i}dp_{l,j-1,k-\binom{i-l}{2}} dpi,j,k=l<i∑dpl,j−1,k−(2i−l)
考虑写成这样的形式
F i , j = ∑ l < i F l , j − 1 ∗ x ( i − l 2 ) F_{i,j}=\sum_{l<i}F_{l,j-1}*x^{\binom{i-l}{2}} Fi,j=l<i∑Fl,j−1∗x(2i−l)
代入 ( n + 1 2 ) + 1 \binom{n+1}{2}+1 (2n+1)+1 个点值就可以插出原多项式,注意到我们强制在最后放一个 n + 1 n+1 n+1,那么只需要对 F n + 1 , 1... n + 1 F_{n+1,1...n+1} Fn+1,1...n+1 共 n + 1 n+1 n+1 个多项式进行 i d f t idft idft,复杂度 O ( n 3 log n ) O(n^3\log n) O(n3logn)
回到上面的转移,发现是个卷积的形式,即
F i , j = ∑ l = 0 i F l , j − 1 c o e f i − l F_{i,j}=\sum_{l=0}^iF_{l,j-1}coef_{i-l} Fi,j=l=0∑iFl,j−1coefi−l
由于代的是点值,所以 c o e f coef coef 可以预先算出来
我们将 c o e f , F j = 0 coef,F_{j=0} coef,Fj=0 d f t dft dft,点乘转移,复杂度 O ( n 2 ) O(n^2) O(n2)
考虑最后只需要知道 x n + 1 x^{n+1} xn+1 的系数,所以我们只需要对 F n + 1 , j = 1... n + 1 F_{n+1,j=1...n+1} Fn+1,j=1...n+1 暴力 O ( n ) O(n) O(n) i d f t idft idft 回去
所以可以在 O ( n 4 ) O(n^4) O(n4) 的时间解决这个问题
B B B
-
考虑如何暴力 D P DP DP,我的做法是记录 d p u , v dp_{u,v} dpu,v 表示 u u u 的子树,从 v v v 接上来一条还没有匹配的链( v = 0 v=0 v=0 表示 u u u向上的边断掉)
发现当 v ≠ 0 v\neq 0 v=0 时,会将每个子树的 d p dp dp 值乘上 ∏ t ≠ v d p t , 0 \prod_{t\neq v}dp_{t,0} ∏t=vdpt,0 然后合并上去(用线段树合并简单维护)
当 v = 0 v=0 v=0 时,先考虑子树中一个点和 u u u 拼接,可以在线段树中查询 ≥ \ge ≥ 某个值的 d p dp dp 和还有一个 ∏ t ≠ v d p t , 0 \prod_{t\neq v}dp_{t,0} ∏t=vdpt,0 的系数,考虑两个子树的拼接,假设 d p v , 0 = 0 dp_{v,0}=0 dpv,0=0 的 v v v 有 k k k 个 -
当 k > 2 k>2 k>2 时不存在这种情况
当 k = 2 k=2 k=2 时,两个都必须选才会有值,必定存在一个轻儿子,我们 d f s dfs dfs 那个轻儿子
当 k = 1 k=1 k=1 时,它必须选,若它是重儿子,我们 d f s dfs dfs 所有轻儿子,否则我们 d f s dfs dfs 除它以外的轻儿子,然后 d f s dfs dfs 它自己与重儿子拼接
当 k = 0 k=0 k=0 时, d f s dfs dfs 所有轻儿子并考虑与前面的拼接, d f s dfs dfs 完后将它的线段树合并上去
C C C
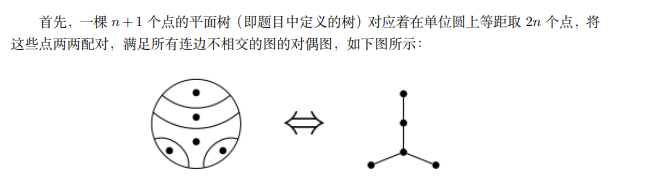
- 以下 n n n 是原问题的 n − 1 n-1 n−1,卡特兰数用 c a t i cat_i cati 表示,我们对 2 n 2n 2n 个置换统计不动点个数
- 容易发现,当 n n n 为偶数时,置换个数必须为偶数
当 n n n 为奇数时,对角线可能匹配,此时的不动点个数是 n ∗ c a t n − 1 2 n*cat_{\frac{n-1}{2}} n∗cat2n−1
设环的个数为 2 d 2d 2d,环的大小为 e e e,考虑求出 f d f_d fd 表示有 2 d 2d 2d 个环的方案数
我们枚举与 1 号相连的点 2 i 2i 2i,它们中间的连边方式为 c a t i − 1 cat_{i-1} cati−1,并且可以确定 i i i 个环的连边方式,于是有
f d = 2 ∑ i = 1 d f d − i c a t i − 1 , f 0 = 1 f ( x ) = 2 f ( x ) c a t ( x ) + 1 f_d=2\sum_{i=1}^df_{d-i}cat_{i-1},f_0=1\\ f(x)=2f(x)cat(x)+1 fd=2i=1∑dfd−icati−1,f0=1f(x)=2f(x)cat(x)+1
由 c a t ( x ) = c a t ( x ) 2 + 1 = 1 − 1 − 4 x 2 x cat(x)=cat(x)^2+1=\frac{1-\sqrt{1-4x}}{2x} cat(x)=cat(x)2+1=2x1−1−4x 可以得到 f ( x ) = ( 1 − 4 x ) − 1 2 f(x)=(1-4x)^{-\frac{1}{2}} f(x)=(1−4x)−21
将其泰勒展开可以知道 [ x i ] f = ( 2 ∗ i i ) [x^i]f=\binom{2*i}{i} [xi]f=(i2∗i),所以可以 O ( σ 0 ( n ) ) O(\sigma_0(n)) O(σ0(n)) 计算答案
这篇关于【省选模拟】20/05/31的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









