Day1 省选衔接题 思路总结

本文主要是介绍Day1 省选衔接题 思路总结，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Day1 省选题 思路

---

取数

可反悔的贪心。我们开一个双向链表记录此时每个数的前/后一个数是什么。一个简单但不一定正确的贪心策略即为：每次都取走当前值最大的且可取的数，并更新列表。考虑如何使这个贪心思路正确。

设 $pr{e}_x$ 表示 $x$ 的前一个元素，$nx{t}_x$ 表示 $x$ 的后一个元素，$w(x)$ 表示 $x$ 的值。则在取走 $x$ 后，显然 $pr{e}_x,nx{t}_x$ 在这之后都不能被选取。**但如果发现选择 $pr{e}_x,nx{t}_x$ 会比只选 $x$ 更优呢？**考虑这个贪心每轮都至少新挑出一个元素出来，那么在选择 $x$ 后放弃 $x$ 选择了 $pr{e}_x,nx{t}_x$，可以理解是将 $x$ 替换为后两者中的一个（反悔操作），并新选出了后两者中的另一个。而将 $x$ 替换为 $pr{e}_x,nx{t}_x$ 的收益为 $w(pr{e}_x)+w(nx{t}_t)-w(x)$，所以我们就可以将这个值也当作一个可选的点，继续进行贪心。

细节部分，在选择了 $x$ 后，可以将链表中的 $x$ 直接替换为 $pr{e}_x,nx{t}_x$ 两点综合起来。具体地，在计算完 $x$ 的贡献后，标记 $nx{t}_x,pr{e}_x$ 这两个单独的点分别标记为已选，然后就可以更新 $w(x)\leftarrow w(pr{e}_x)+w(nx{t}_t)-w(x)$。因为 $nx{t}_x,pr{e}_x$ 都不能再单独被选，所以按照正常的链表删除操作删除 $pr{e}_x,nx{t}_x$ 两个单独的点。

取数2

题意即为：从 $n$ 个集合中各选出一个数求和，求出前 $k$ 大的和。为了顺应大家的习惯，这里将 $n,k$ 的意义调换了。

显然最大的取法就是从每个集合中取一个最大值求和，我们设这个最优值为 $ans$。考虑其可能的后几个略小一些的状态。我们将每个集合按照最大值减次大值的差从小到大排序，每个集合内部按从大到小排序。假设当前状态 { i , j , w } \{i,j,w\} {i,j,w} 表示枚举到第 $i$ 个集合中的第 $j$ 个数，考虑将 $ans$ 中第 $i$ 个集合取的数更换为 $j$，更换后的答案为 $w$。令 $c(i,j)$ 表示集合 $i$ 中第 $j$ 大的值，最初始的状态即为 { 1 , 2 , a n s − c ( 1 , 1 ) + c ( 1 , 2 ) } \{1,2,ans-c(1,1)+c(1,2)\} {1,2,ans−c(1,1)+c(1,2)}。对于每个状态会有三个可能的分支：

• 如果 $j<si{z}_i$，则一种可能的选择即为放弃更换为 $j$，考虑更换为 $j+1$。新的状态为 { i , j + 1 , w − c ( i , j ) + c ( i + j ) } \{i,j+1,w-c(i,j)+c(i+j)\} {i,j+1,w−c(i,j)+c(i+j)}。
• 如果 $i$ 不是最后一个集合：
  • 一种可能的选择即为决定更换为 $j$，开始考虑 $i+1$ 集合的选择。新的状态为 { i + 1 , 2 , w − c ( i + 1 , 1 ) + c ( i + 1 , 2 ) } \{i+1,2,w-c(i+1,1)+c(i+1,2)\} {i+1,2,w−c(i+1,1)+c(i+1,2)}。
  • 另外，如果 $j=2$，则一种可能的选择即为放弃更换 $i$ 中的元素，直接考虑 $i+1$ 集合的选择。新的状态为 { i + 1 , 2 , w − c ( i , 2 ) + c ( i , 1 ) − c ( i + 1 , 1 ) + c ( i + 1 , 2 ) } \{i + 1,2,w - c(i,2) + c(i,1) - c(i+1,1) + c(i+1,2)\} {i+1,2,w−c(i,2)+c(i,1)−c(i+1,1)+c(i+1,2)}。

开一个优先队列记录这些状态，从中取 $k$​ 轮即为答案。

文件列表

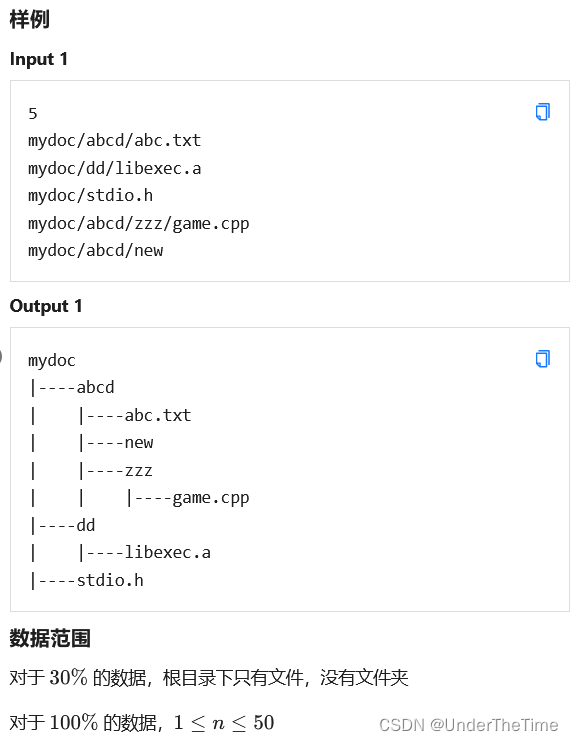
可以说是 C++ 语法题

直接按照题意模拟即可，注意文件（夹）名可能会重复。

巧置挡板

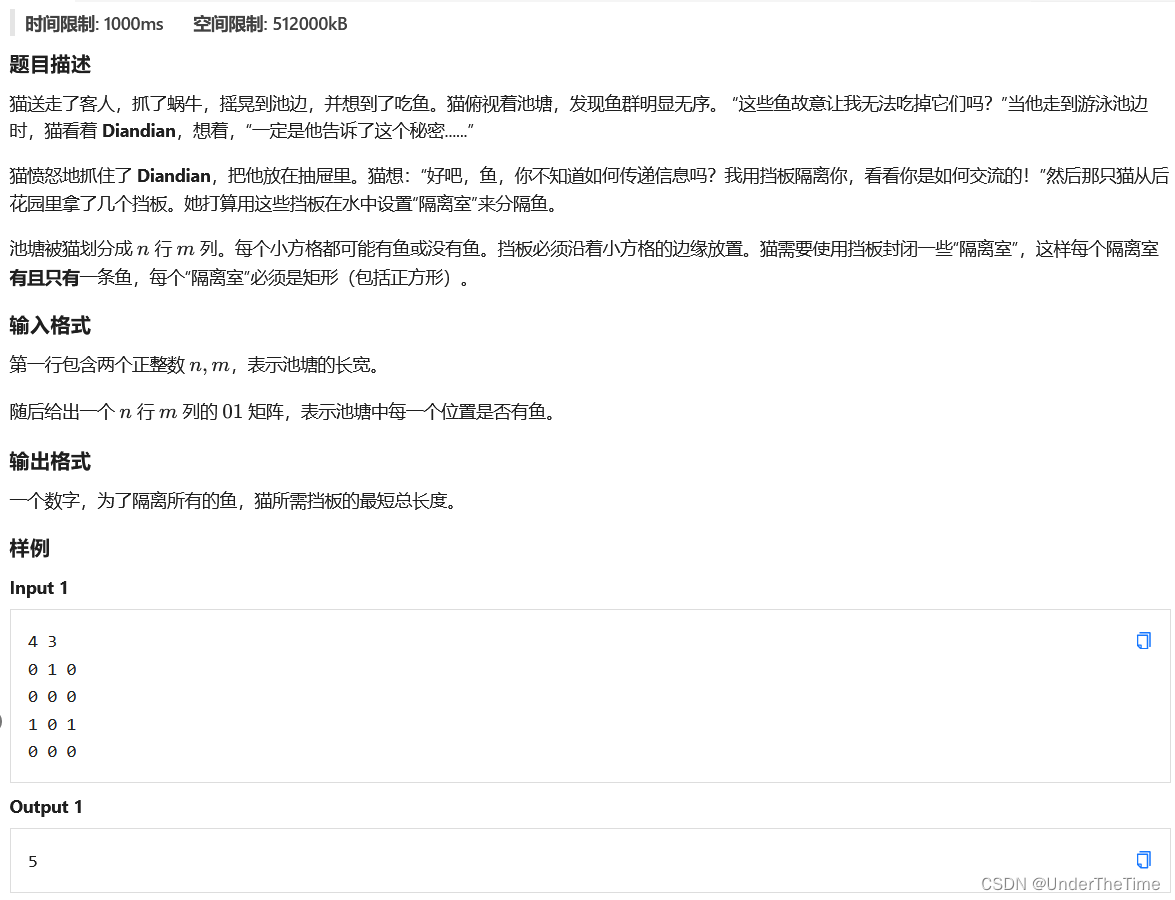
暴搜+剪枝。由于最终每一个矩形中都有且仅有一个 $1$，我们不妨在搜索的过程中，每次枚举所有包含某一个 $1$ 的矩形。状态可以这样设计，我们用一个长度为 $n$ 的序列来表示一条从右上到左下的单调分界线（序列中每一个元素表示该行分界线的位置），分界线左边为搜索过的区域，右边为未搜索的区域。这个状态的答案将表示完成右侧区域最少的边数。

为什么是单调的分界线？在任意一种分隔方案中，都一定存在一种矩形放置顺序，使得每次放置之后，分界线仍然是单调的。所以即使是仅考虑单调的分界线状态，也一定可以搜索到所有状态，这样可以简化状态降低复杂度。然而这样复杂度仍然较高。这里给出几种：剪枝的手段：

• 状态可以记忆化，哈希之后用 map 存储；
• 假设某一行有一个折角（分界线相比上一行发生左移），如果折角的右下方没有一个 $1$，则一定会出现空矩形，不合法；
• 枚举当前矩形时，$1$ 的个数超过 $1$ 后可以直接停止，不合法。

这篇关于Day1 省选衔接题 思路总结的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---