本文主要是介绍【省选模拟】20/06/05,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
A A A
-
l d x ldx ldx 大神的 60 60 60 分做法:
用二元组 ( a , b ) (a,b) (a,b) 记录最小段数和最小代价来 d p dp dp,记 d p i dp_i dpi 表示以 i i i 结尾的最小值
考虑如何为一个区间选择一个最优的匹配点,暴力枚举 d p j dp_j dpj,考虑将某一个区间从 j j j 挪到 i i i,这对应一个关于 i , j i,j i,j 的二元一次函数,用三元组 ( a , b , c ) (a,b,c) (a,b,c) 可以表示出这个系数
系数预处理是个二维平面修改,差分后求矩阵的前缀和,可以做到 O ( n 2 ) O(n^2) O(n2) -
这个 d p dp dp 看起来不能优化了,考虑一些性质,设贪心出来选出来的点为 p 1 , p 2 , … , p k p_1,p_2,\dots,p_k p1,p2,…,pk,那么 ( p 0 , p 1 ] , ( p 1 , p 2 ] , … , ( p k − 1 , p k ] (p_0,p_1],(p_1,p_2],\dots,(p_{k-1},p_k] (p0,p1],(p1,p2],…,(pk−1,pk] 的每个区间必然存在且仅存在一个点,显然大于一个点是不可能的,若存在一个区间没有点,那么必定存在一个区间满足 l i ∈ ( p t − 1 , p t ] , r i = p t l_i\in (p_{t-1},p_t],r_i=p_t li∈(pt−1,pt],ri=pt,不合法
-
同时注意到,一个区间的中点必定可以定位到两个点之间,且最优值只会取到两个端点的一个
前缀和简单询问每个区间的系数 c o e f l , r coef_{l,r} coefl,r,于是可以暴力 d p dp dp:
d p i = min d p j + c o e f j , i ( j ∈ ( p t − 1 , p t ] ) dp_{i}=\min dp_j+coef_{j,i}(j\in(p_{t-1},p_t]) dpi=mindpj+coefj,i(j∈(pt−1,pt]),又注意到对于 c o e f i , r , c o e f j , r ( i < j ) coef_{i,r},coef_{j,r}(i<j) coefi,r,coefj,r(i<j), i i i 的增量始终大于 j j j 的增量,可以分治解决
#include<bits/stdc++.h>
#define cs const
#define pb push_back
#define fi first
#define se second
using namespace std;
namespace IO{cs int Rlen=1<<22|1;inline char gc(){static char buf[Rlen],*p1,*p2;(p1==p2)&&(p2=(p1=buf)+fread(buf,1,Rlen,stdin));return p1==p2?EOF:*p1++;} int read(){int x=0; char c=gc(); bool f=false;while(!isdigit(c)) f=c=='-', c=gc();while(isdigit(c)) x=(((x<<2)+x)<<1)+(c^48), c=gc();return f?-x:x;}
} using namespace IO;
typedef long long ll;
cs ll INF = 1e18;
void ckmin(int &a, int b){ if(a > b) a = b; }
void ckmax(int &a, int b){ if(a < b) a = b; }
cs int N = 2e6 + 50;
struct my{ int l, r; };
bool cmp(cs my &a, cs my &b){ return a.l < b.l || (a.l == b.l && a.r > b.r); }
int n, m, Ans; my a[N], b[N];
int rp[N], A; ll Sm[N]; int ct[N];
ll dp[N]; int lm[N], mx[N];
ll calc(int l, int r){if(l==0) return (ll)r*ct[r]-Sm[r];if(r>A) return Sm[r]-Sm[l]-(ll)l*(ct[r]-ct[l]);int mid = (l+r)>>1; assert(l<=r);ll lv = Sm[mid]-Sm[l]-(ll)l*(ct[mid]-ct[l]);ll rv = (ll)r*(ct[r]-ct[mid])-(Sm[r]-Sm[mid]);return lv + rv;
}
void work(int L, int R, int l, int r){if(L>R) return; int mid = (L+R) >> 1;int trs = 0; ll mn = INF;for(int i = max(lm[mid],l); i <= r; i++){ll t = dp[i] + calc(i,mid);if(t < mn) mn = t, trs = i;} dp[mid] = mn;work(L,mid-1,l,trs); work(mid+1,R,trs,r);
}
int main(){#ifdef FSYolandafreopen("1.in","r",stdin);#endifscanf("%d",&n);for(int i=1; i<=n; i++)a[i].l=read()<<1, a[i].r=read()<<1, A=max(A,a[i].r);sort(a+1,a+n+1,cmp);for(int i=1; i<=n; i++){while(m && a[i].r <= b[m].r) --m;b[++m] = a[i];} for(int l=1,r=1;l<=m;l=r){while(r<=m&&b[r].l<=b[l].r) ++r;++Ans; rp[Ans] = b[l].r;} rp[Ans+1] = A+1; for(int i=1,x; i<=n; i++){x=(a[i].l+a[i].r)>>1;++ct[x]; Sm[x]+=x;} for(int i=1; i<=A+1; i++) Sm[i]+=Sm[i-1],ct[i]+=ct[i-1];for(int i=1; i<=rp[1]; i++) dp[i] = calc(0,i);for(int i=1; i<=n; i++) mx[a[i].r]=max(mx[a[i].r],a[i].l);for(int i=1,lp=0; i<=A+1; i++) lm[i]=lp, lp=max(lp,mx[i]);for(int i=1; i<=Ans; i++) work(rp[i]+1,rp[i+1],rp[i-1]+1,rp[i]);cout << Ans << " " << dp[A+1];return 0;
}
B B B
- 点分树即可,用 z k w zkw zkw 线段树维护一下子树的某个区间的最近距离, O ( n log 2 n ) O(n\log^2 n) O(nlog2n),可以跑过 O ( n log n ) O(n\log n) O(nlogn) 的线段树分治 + 虚树
#include<bits/stdc++.h>
#define cs const
#define pb push_back
#define fi first
#define se second
using namespace std;
namespace IO{cs int Rlen=1<<22|1;inline char gc(){static char buf[Rlen],*p1,*p2;(p1==p2)&&(p2=(p1=buf)+fread(buf,1,Rlen,stdin));return p1==p2?EOF:*p1++;} int read(){int x=0; char c=gc(); bool f=false;while(!isdigit(c)) f=c=='-', c=gc();while(isdigit(c)) x=(((x<<2)+x)<<1)+(c^48), c=gc();return f?-x:x;}
} using namespace IO;
cs int N = 1e5 + 50;
cs int INF = 1e9 + 7;
int n, m, fi[N], nxt[N<<1], to[N<<1], w[N<<1], ec;
void adde(int u, int v, int c){ nxt[++ec]=fi[u]; fi[u]=ec; to[ec]=v; w[ec]=c;
}
int d[18][N], fa[N], dep[N];
int sz[N], mx, rt; bool ban[N];
void gsz(int u, int fa){sz[u]=1;for(int e=fi[u],v;e;e=nxt[e])if(!ban[v=to[e]]&&to[e]!=fa)gsz(v,u),sz[u]+=sz[v];
}
void grt(int u, int fa){int now=sz[0]-sz[u];for(int e=fi[u],v;e;e=nxt[e])if(!ban[v=to[e]]&&to[e]!=fa)grt(v,u),now=max(now,sz[v]);if(now<mx) mx=now,rt=u;
}
void dfs(int dt, int u, int fa){for(int e=fi[u],v;e;e=nxt[e])if(!ban[v=to[e]]&&to[e]!=fa)d[dt][v]=d[dt][u]+w[e],dfs(dt,v,u);
}
vector<int> G[N];
void work(int u, int an, int d){gsz(u,0); sz[0]=mx=sz[u]; rt=0; grt(u,0);ban[u=rt]=true; fa[u]=an; dep[u]=d; dfs(d,u,0); if(an) G[an].pb(u);for(int e=fi[u];e;e=nxt[e])if(!ban[to[e]]) work(to[e],u,d+1);
}
struct qry{ int d, l, r, c; };
vector<qry> S[N]; int ans[N];
void jmp(int x, int l, int r, int c){for(int u=x;u;u=fa[u])S[u].pb((qry){d[dep[u]][x],l,r,c});
}
namespace zkw{cs int M = 1 << 17;int mn[M<<1];void init(){ memset(mn,0x3f,sizeof(mn)); }void ins(int x, int v){ for(x+=M;x;x>>=1)mn[x]=min(mn[x],v); }void clr(int x){ for(x+=M;x;x>>=1)mn[x]=INF; }int qry(int l, int r){int ans=INF; for(l+=M-1,r+=M+1;l^r^1;l>>=1,r>>=1){if(l&1^1) ans=min(ans,mn[l^1]);if(r&1) ans=min(ans,mn[r^1]);} return ans;}}
void subwork(int u, int dt){zkw::ins(u,d[dt][u]); for(int e=0;e<G[u].size();e++)subwork(G[u][e],dt);
}
void _subwork(int u){zkw::clr(u);for(int e=0;e<G[u].size();e++)_subwork(G[u][e]);
}
void work(int u){subwork(u,dep[u]);for(int i=0;i<S[u].size();i++){qry t=S[u][i];ans[t.c]=min(ans[t.c],zkw::qry(t.l,t.r)+t.d);} _subwork(u);
}
int main(){freopen("tree.in","r",stdin);freopen("tree.out","w",stdout);n=read(); zkw::init();for(int i=1,u,v,w;i<n;i++)u=read(),v=read(),w=read(),adde(u,v,w),adde(v,u,w); work(1,0,0); m=read();for(int i=1,l,r,x; i<=m; i++){l=read(), r=read(), x=read();jmp(x,l,r,i); ans[i]=INF;} for(int i=1; i<=n; i++)if(S[i].size())work(i);for(int i=1; i<=m; i++) cout << ans[i] << '\n';return 0;
}
C C C
- 枚举点积角度可以死去
- 考虑一个等价的过程,枚举一条边以及角度,积有贡献的点集的面积

- 变成积一个前缀的面积,发现每次要处理的就是 ∫ S B C D d C \int S_{BCD}\text{d}C ∫SBCDdC
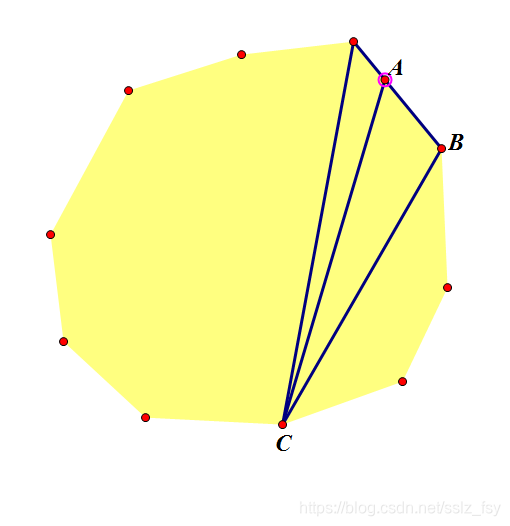
- 而 B C sin B + C = A B sin C \frac{BC}{\sin B+C}=\frac{AB}{\sin C} sinB+CBC=sinCAB, S = A B ∗ B C ∗ sin B = t ∗ sin C sin B + C S=AB*BC*\sin B=t*\frac{\sin C}{\sin B+C} S=AB∗BC∗sinB=t∗sinB+CsinC 其中 t t t 为常量,考虑积分:
∫ 0 R sin C sin B + C d C = cos B ∗ R − sin B ∫ B R + B cos C sin C d C \int_0^{R}\frac{\sin C}{\sin B+C}\text{d}C\\ =\cos B *R- \sin B\int_B^{R+B}\frac{\cos C}{\sin C}\text{d}C ∫0RsinB+CsinCdC=cosB∗R−sinB∫BR+BsinCcosCdC
∫ cos x sin x d x = ∫ 1 sin x d sin x = ln sin x \int \frac{\cos x}{\sin x}\text{d}x=\int \frac{1}{\sin x}\text{d}\sin x=\ln \sin x ∫sinxcosxdx=∫sinx1dsinx=lnsinx
#include<bits/stdc++.h>
#define cs const
#define pb push_back
#define fi first
#define se second
using namespace std;
namespace IO{cs int Rlen=1<<22|1;inline char gc(){static char buf[Rlen],*p1,*p2;(p1==p2)&&(p2=(p1=buf)+fread(buf,1,Rlen,stdin));return p1==p2?EOF:*p1++;} int read(){int x=0; char c=gc(); bool f=false;while(!isdigit(c)) f=c=='-', c=gc();while(isdigit(c)) x=(((x<<2)+x)<<1)+(c^48), c=gc();return f?-x:x;}
} using namespace IO;
cs int N = 3e3 + 50;
cs double eps = 1e-8, PI = acos(-1.0);
int sgn(double a){ return (a>eps) - (a<-eps); }
struct pnt{double x, y; pnt(double _x=0, double _y=0){ x=_x; y=_y; }void input(){ x=read(); y=read(); }void output(){ cout << x <<" " << y << '\n'; }pnt operator + (cs pnt &a){ return pnt(x+a.x,y+a.y); }pnt operator - (cs pnt &a){ return pnt(x-a.x,y-a.y); }double operator * (cs pnt &a){ return x*a.y-y*a.x; }pnt operator * (cs double &a){ return pnt(x*a,y*a); }double Len(){ return x * x + y * y; }double len(){ return sqrt(x*x+y*y); }double ang(){ return atan2(y,x); }
};
int n; pnt p[N]; double ans[N];
double ang(pnt a, pnt b, pnt c){return acos(((b-a).Len()+(c-b).Len()-(c-a).Len())/(2*(c-b).len()*(b-a).len()));
}
int main(){#ifdef FSYolandafreopen("1.in","r",stdin);#endifn=read();for(int i=1; i<=n; i++) p[i].input(),p[i+n]=p[i]; double S=0;for(int i=1; i<=n; i++)S+=p[i]*p[i+1];for(int i=1; i<=n; i++){double now = 0;for(int j=i+1; j<i+n-1; j++){double a = ang(p[j],p[i],p[j+1]);double b = ang(p[i],p[j],p[j+1]);ans[i] += a * now + (p[i]-p[j]).Len() * sin(b) * (a * cos(b) - sin(b) * (log(fabs(sin(a+b))) - log(fabs(sin(b)))));now += (p[j]-p[i]) * (p[j+1]-p[i]);}}for(int i=1; i<=n; i++){double Ans = ans[i] - ans[i%n+1];Ans += (PI - ang(p[i+n-1],p[i],p[i+1])) * S;printf("%.8lf\n",Ans/S/PI/2);} return 0;}
这篇关于【省选模拟】20/06/05的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









