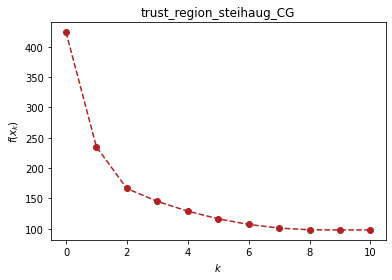
无约束专题
【文献精读】基于驱动力表的无人车终端无约束预测纵向控制(TVT)
写在前面: 🌟 欢迎光临 清流君 的博客小天地,这里是我分享技术与心得的温馨角落。📝 个人主页:清流君_CSDN博客,期待与您一同探索 移动机器人 领域的无限可能。 🔍 本文系 清流君 原创之作,荣幸在CSDN首发🐒 若您觉得内容有价值,还请评论告知一声,以便更多人受益。 转载请注明出处,尊重原创,从我做起。 👍 点赞、评论、收藏,三连走一波,让我们一起养成好习惯😜 在这里,您将
基于估计的无约束预测控制
这一节讨论状态不是全部可以测量或有测量噪声的情况下,基于状态估计的无约束预测控制。 一、状态估计 如果状态不是全部可以测量或有测量噪声,则需要估计状态或滤波。设系统的可测量输出变量 y m ( k ) = C m x ( k ) y_m(k)=C_mx(k) ym(k)=Cmx(k) 考虑下面的估计器形式: x ^ ( k + 1 ) = A x ^ ( k ) + B u u (
修正牛顿法求解无约束问题
function [x,val,k]=revisenm(fun,gfun, Hess, x0) %功能:用修正牛顿法求解无约束问题:min f(x) %输入:x0是初始点,fun, gfun,Hess分别是求目标函数值,梯度,Hesse矩阵的函数 %输出:x,val分别是近似最优点和最优值,k是迭代次数 n=length(x0);maxk=150; rho=0.55;sigma=0.4;t
【matlab基础知识代码】(十八)无约束最优化问题
min下面的x称为优化向量或者是决策变量 匿名函数法 >> f=@(x)(x(1)^2-2*x(1))*exp(-x(1)^2-x(2)^2-x(1)*x(2)); x0=[0; 0]; [x,b,c,d]=fminsearch(f,x0), x = 0.6111 -0.3056 b = -0.6414 c = 1 d =
MATLAB多维无约束最小化函数 fminunc 、fminsearch与多维有约束函数fmincon
一、多维无约束最小化函数 fminunc 1、函数模型 ,式中f(x)为无约束多变量函数,x是向量或矩阵 2、调用格式 x = fminunc(fun,x0) matlab代码 %% 多维无约束极值f=@(x) (x(1)^2+2*x(1))*exp(-x(1)^2-x(2)^2-x(1)*x(2))x0=[0 0];[x,favl]=fminunc(f,x0)%绘制处函数图形,
MATLAB无约束多维极值之坐标轮换法
一、算法原理 坐标轮换法亦称变量轮换法时一种求无约束最优化问题的降维方法.其迭代过程是沿不同的坐标方向轮换地进行搜索. 例 二维极值 设初始点为x0=[1,1],先只改变一个变量,其他变量视为常数,进行一维搜索,得到最优点x01: x01=x0+e1*a,式中e1=[0,1]为方向,a为待求步长。通过min f(x0+e1*a)求得最优步长。 (通过进退法求得极值区间,黄金分割法求得最优
无约束最优化方法-牛顿法
无约束最优化算法-Newton法原理及c++编程实现 2012-12-14 13:04 6536人阅读 评论(5) 收藏 举报 本文章已收录于: 分类: 【算法】(27) 作者同类文章 X 版权声明:本文为博主原创文章,未经博主允许不得转载。 无约束最优化方法-牛顿法 牛顿法(Newton'smethod)又称为牛
无约束优化算法之拟牛顿法
拟牛顿法 牛顿法在理论上有很好的效果,然而对于大规模问题,函数的海塞矩阵计算待解特别大或者难以得到,即便得到海塞矩阵我们还需要求解一个大规模线性方程组。那么能否使用海塞矩阵或其逆矩阵的近似来进行牛顿迭代呢?拟牛顿法便是这样的算法,它能够在每一步以较小的代价生成近似矩阵,并且使用近似矩阵代替海塞矩阵,而产生的迭代序列仍具有超线性收敛的性质。 拟牛顿法不计算海塞矩阵 ∇ 2 f ( x ) \nab
运筹说 第98期|无约束极值问题
上一期我们一起学习了关于非线性规划问题的一维搜索方法的相关内容,本期小编将带大家学习非线性规划的无约束极值问题。 下面,让我们从实际问题出发,学习无约束极值问题吧! 一、问题描述及求解原理 1 无约束极值问题的定义 无约束极值问题可表述为 在求解上述问题时常使用迭代法。 2 迭代法 迭代法的基本思想:在一个近似点处选定一个有利搜索方向,沿这个方向进行一维寻查,得出新的近似点。
【最优化方法】无约束优化问题(函数梯度、下降方向、最优性)
文章目录 下降方向下降方向与梯度关系例题偏导数方向导数梯度(导数)下降方向 最优性条件一阶必要条件二阶必要条件二阶充分条件无约束凸规划的最优性条件 我们把一元方程推广到 n n n 维无约束极小化问题,得到解无约束优化问题 min x ∈ R n f ( x ) \min_{x\in\mathbf{R}^n}f(x) x∈Rnminf(x) 下降方向 设 f (
最优化方法Python计算:无约束优化应用——神经网络回归模型
人类大脑有数百亿个相互连接的神经元(如下图(a)所示),这些神经元通过树突从其他神经元接收信息,在细胞体内综合、并变换信息,通过轴突上的突触向其他神经元传递信息。我们在博文《最优化方法Python计算:无约束优化应用——逻辑回归模型》中讨论的逻辑回归模型(如下图(b)所示)与神经元十分相似,由输入端接收数据 x = ( x 1 x 2 ⋮ x n ) \boldsymbol{x}=\begin{p
最优轨迹生成(三)—— 无约束BIVP轨迹优化
本系列文章是学习深蓝学院-移动机器人运动规划课程第五章最优轨迹生成 过程中所记录的笔记,本系列文章共包含四篇文章,依次介绍了微分平坦特性、无约束BVP轨迹优化、无约束BIVP轨迹优、 带约束轨迹优化等内容 本系列文章链接如下: 最优轨迹生成(一)—— 微分平坦 最优轨迹生成(二)—— 无约束BVP轨迹优化 最优轨迹生成(三)—— 无约束BIVP轨迹优化
最优化方法Python计算:无约束优化应用——逻辑分类模型
逻辑回归模型更多地用于如下例所示判断或分类场景。 例1 某银行的贷款用户数据如下表: 欠款(元)收入(元)是否逾期17000800Yes220002500No350003000Yes440004000No520003800No 显然,客户是否逾期(记为 y y y)与其欠款额(记为 x 1 x_1 x1)和收入(记为 x 2 x_2 x2)相关。如果将客户逾期还款记为1,未逾期记为0,我们
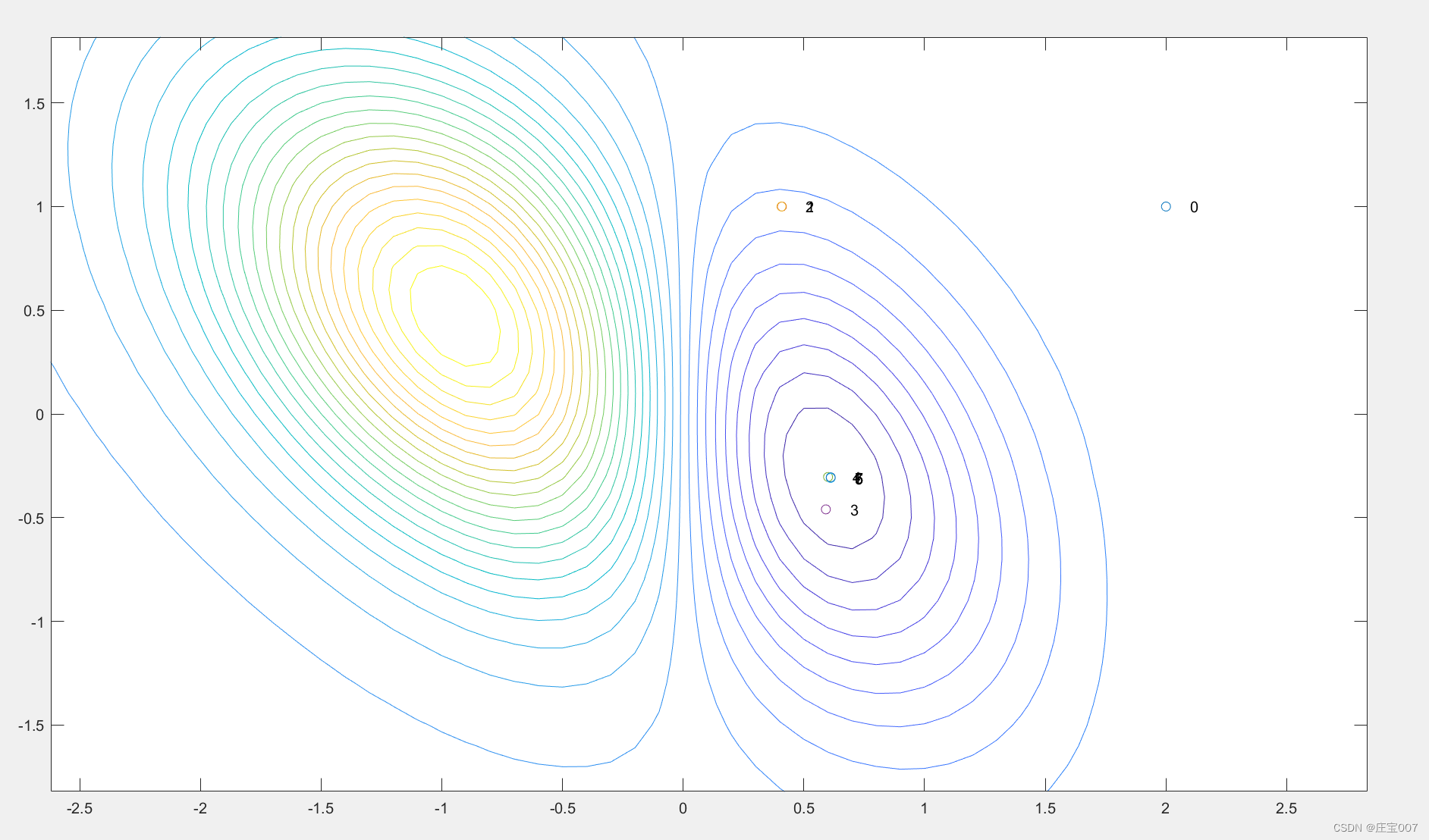
[最优化导论]C6 集合约束和无约束优化问题
集合约束和无约束优化问题 集合约束和无约束优化的基本形式为: m i n i m i z e f ( x ) s u b j e c t t o x ∈ Ω \begin{aligned} minimize f(\mathbf{x}) \\ subject\ \ to\ \ \mathbf{x}\in\Omega\end{aligned} minimizef(x)subject to x
无约束优化问题求解(4):牛顿法
目录 5.牛顿法5.1 基本牛顿法5.1.1 牛顿法的定义5.1.2 牛顿法的性质5.1.3 牛顿法的优缺点 5.2 阻尼牛顿法5.3 拟牛顿法5.3.1 拟牛顿法基本思想5.3.2 拟牛顿法的求解构造秩1校正秩2校正 Reference 5.牛顿法 5.1 基本牛顿法 5.1.1 牛顿法的定义 牛顿法的基本原理是对目标函数在当前点的局部邻域采用二次多项式 q ( x
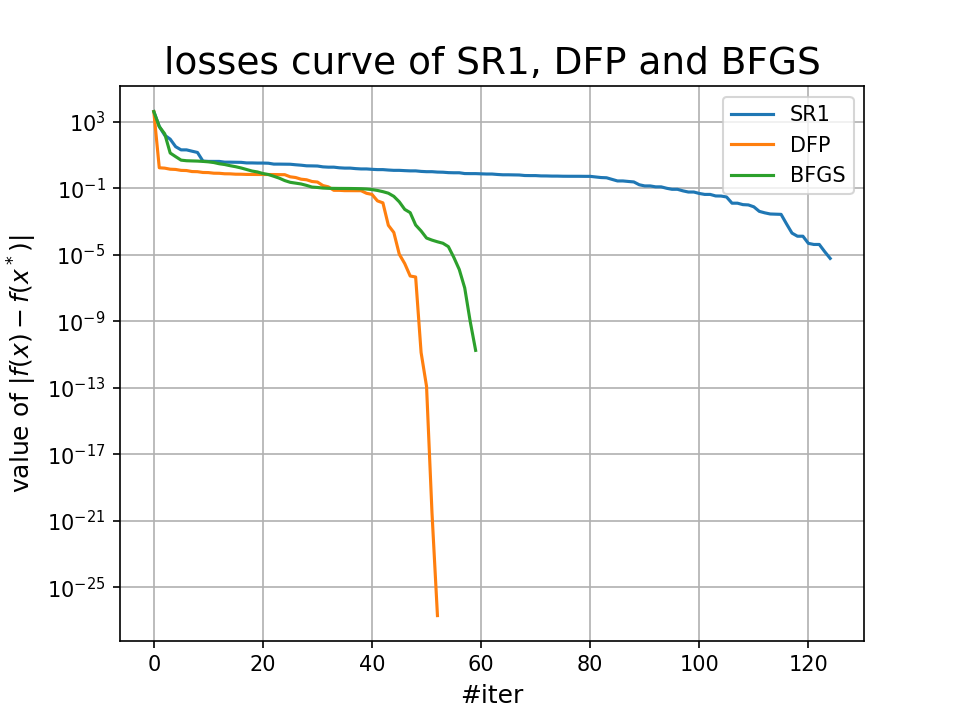
无约束优化问题求解(4):牛顿法后续
目录 前言SR1, DFP, BFGS之间的关系 BB方法Reference 前言 Emm,由于上一篇笔记的字数超过了要求(这还是第一次- -),就把后续内容放到这篇笔记里面了,公式的标号仍然不变,上一篇笔记的连接在这:无约束优化问题求解(4):牛顿法 SR1, DFP, BFGS之间的关系 首先给出如下SMW公式: 考虑到 B k B_k Bk 才是对Hessi
最优化大作业(二): 常用无约束最优化方法
问题描述 对以下优化问题 选取初始点,分别用以下方法求解 (1)最速下降法; (2)Newton法或修正Newton法; (3)共轭梯度法。 基本原理 (1)最速下降法 图1 最速下降法流程图 (2)Newton法 图2 Newton法流程图
无约束一维极值——进退法
前言 在求解目标函数的极小值的过程中,若对设计变量的取值范围不加限制,称这种最优化问题为无约束优化问题。尽管对于机械的优化设计问题,多数是有约束的,但无约束最优化方法仍然是最优化设计的基本组成部分。因为约束最优化问题可以通过对约束条件的处理,转化为无约束最优化问题来求解。 无约束一维极值问题求解时一般采用一维搜索法,其中方法包括多种。线性搜索包括黄金分割、斐波那契法、牛顿法等,非线性搜索包括抛
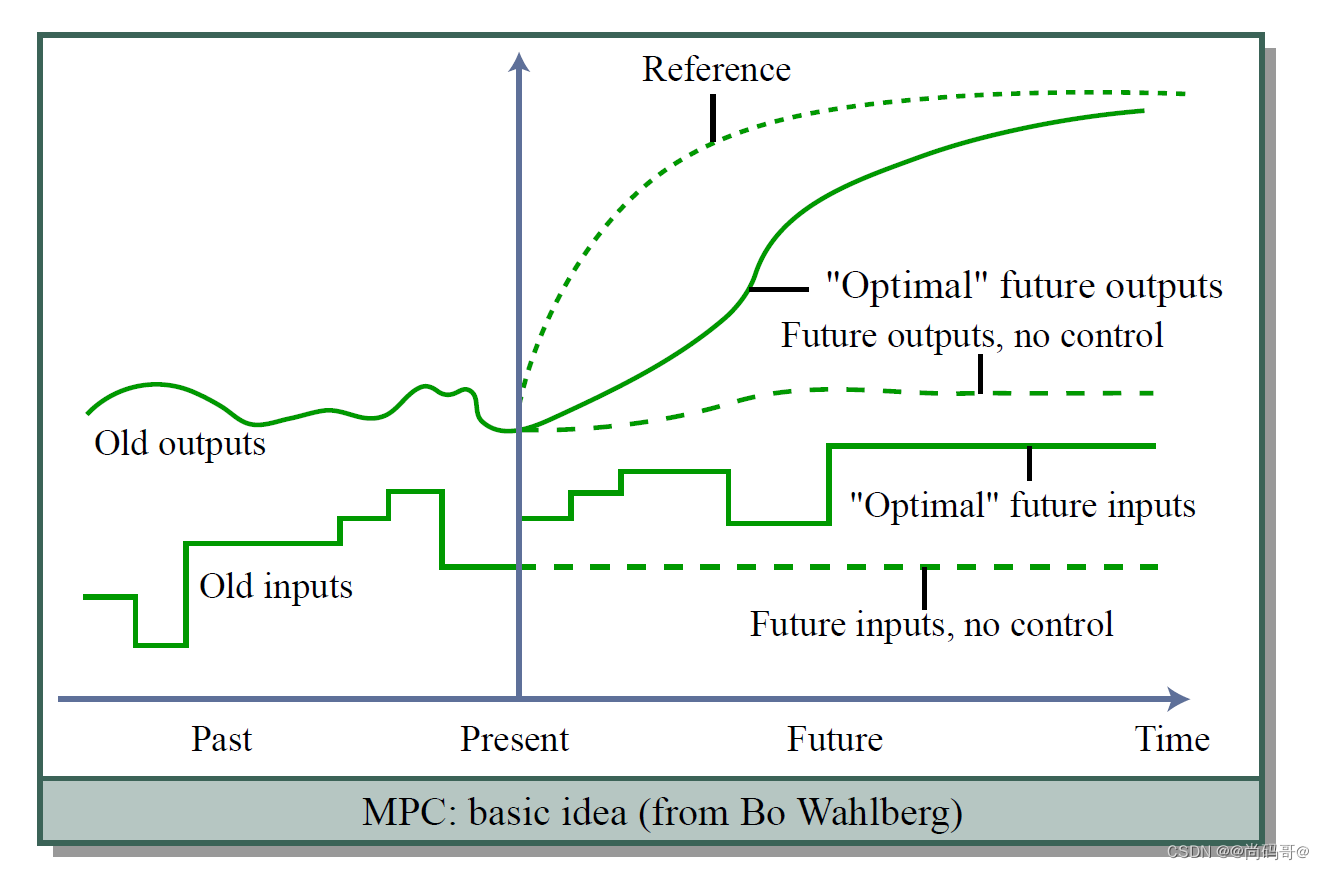
简单入门--无约束线性模型预测控制
简单入门--无约束模型预测控制 一、模型预测控制是什么?1. 引言2. 模型预测控制基础3. MPC数学模型 二、无约束线性模型预测控制1. 无约束线性模型预测控制问题-----标准型2. 无约束线性模型预测控制问题-----紧凑型3. 无约束线性模型预测控制问题-----解析解4. MATLAB 代码示例 导读:下棋有高手和菜鸟,高手往往预测未来多步棋局发展,提前布局,而菜
【最优化方法】无约束非线性函数
向量投影证明 b 1 = d ∗ a 1 ∣ a 1 ∣ d = ∣ a 2 ∣ ∗ c o s θ c o s = ( a 2 , a 1 ) ∣ a 2 ∣ ∣ a 1 ∣ b_1 = d * \frac{a_1}{|a_1|} \\ d = |a_2| * cos\theta \\ cos = \frac{(a_2,a_1)}{|a_2||a_1|} b1=d∗∣a1∣a1d
c语言最优步长坐标轮换法,无约束优化方法-直接方法(坐标轮换法)
无约束最优化方法的一般步骤可以总结如下: 选择初始点 ,这一点越靠近局部极小点 越好; 已取得某设计点 ,选择一个设计方向 ,沿此方向搜索,函数值需是下降的, 是下降方向; 从 出发,沿 方向进行搜索,确定步长因子 ,得到新的设计点 , 并满足
《数学基础》-4.凸优化-4.1.无约束优化
4.1.无约束优化 4.1.1.无约束优化问题 无约束优化问题是机器学习中最普遍、最简单的优化问题。 求最大值也可以 在前面加上负号,变成上面求最小的形式。 求一个函数f(x)的最小值可以对函数f(x)求导并使其等于0(或者说使得梯度▽f(x)等于0),但是很多复杂的函数求导后没法求出解,所以这种方法实际上很少用。 常用梯度下降法、牛顿法或者拟牛顿法求解。 4.1.2.梯度下降法
无约束优化方法(optimtool.unconstrain)
import optimtool as oofrom optimtool.base import np, sp, plt pip install optimtool >=2.4.2 无约束优化方法(optimtool.unconstrain) import optimtool.unconstrain as ouou.[方法名].[函数名]([目标函数], [参数表], [初始迭代点]





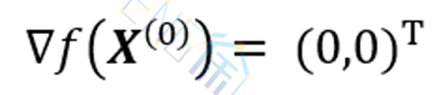



![[最优化导论]C6 集合约束和无约束优化问题](https://img-blog.csdnimg.cn/20190720140743240.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9xeWxpYW5nLmJsb2cuY3Nkbi5uZXQ=,size_16,color_FFFFFF,t_70)