本文主要是介绍简单入门--无约束线性模型预测控制,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
简单入门--无约束模型预测控制
- 一、模型预测控制是什么?
- 1. 引言
- 2. 模型预测控制基础
- 3. MPC数学模型
- 二、无约束线性模型预测控制
- 1. 无约束线性模型预测控制问题-----标准型
- 2. 无约束线性模型预测控制问题-----紧凑型
- 3. 无约束线性模型预测控制问题-----解析解
- 4. MATLAB 代码示例
导读:下棋有高手和菜鸟,高手往往预测未来多步棋局发展,提前布局,而菜鸟只根据当前棋局做选择,显然前瞻不够。模型预测控制有相似的思想。根据当前棋局形势(即系统当前状态)和可能的棋局走势(基于模型预测未来发展),为赢得棋局(根据期望目标),根据自己的经验得出未来多步最优的下棋方案(根据优化方法得出多步最优策略),选择得出的多步最优策略的第一步作为当前步最优决策。并且每次下棋之前都重复上步骤做出最优决策。
一、模型预测控制是什么?
1. 引言
模型预测控制(Model Predictive Control,MPC)是一种先进的控制策略,广泛应用于工业过程、自动驾驶、机器人控制等领域。MPC通过数学模型预测未来系统行为,并优化控制输入,以最优化某些性能指标。
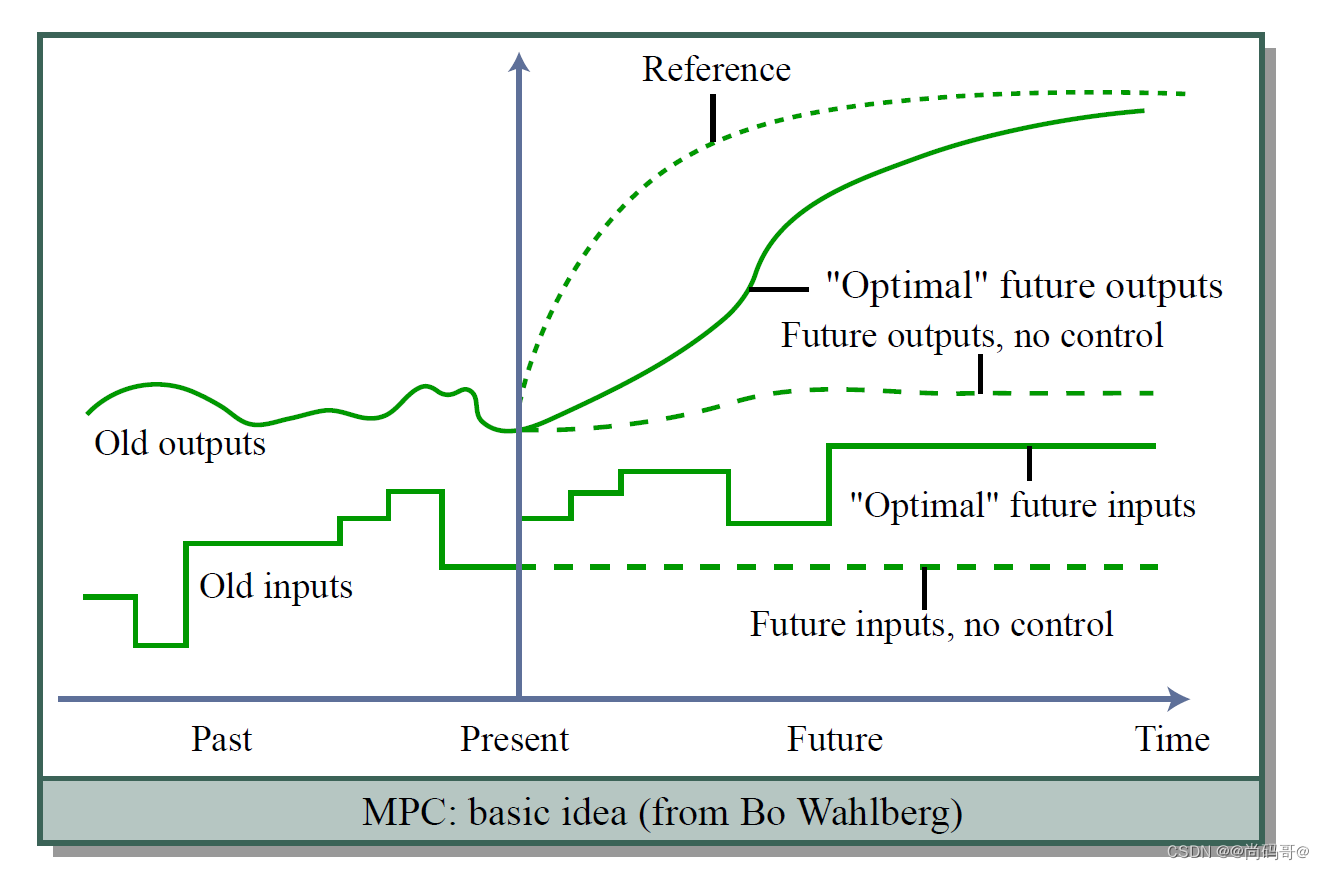
2. 模型预测控制基础
MPC的五要素:
-
系统建模:将被控制系统建模成离散或连续时间的状态空间模型,通常表示为状态方程和输出方程。
-
性能指标定义:确定性能指标,例如最小化误差、能耗或最大化系统效率等,以评估控制器的性能。
-
未来预测:使用系统模型进行未来状态和输出的预测,通常通过数值求解器进行。
-
优化问题:在每个控制步骤中,通过求解优化问题来选择控制输入,以最小化性能指标。这是MPC的关键步骤。
-
应用控制输入:将最优控制输入应用于系统,然后重复上述步骤。
模型预测控制具体应用步骤:
1)基于当前系统状态及模型预测系统未来走向
2)根据期望目标,通过优化的方法得出当前及未来多步最优策略
3)将得出的多步最优策略中的第一步作为当前最优决策。
4)每步决策之前,重复上述方案,随时间逐步推进。
因此模型预测控制也成后退时域控制。
3. MPC数学模型
min u J ≜ F ( x N ) + ∑ i = 0 N − 1 L ( x k + i ∣ k , u k + i ∣ k ) 目标函数 s.t.: x k + i + 1 ∣ k = f ( x k + i ∣ k , u k + i ∣ k ) 系统模型 x k + i ∣ k ∈ X 状态约束 u k + i ∣ k ∈ U 控制约束 x k ∣ k = x k 当前系统状态 u = [ u k ∣ k , … , u k + i ∣ k , … , u k + N − 1 ∣ k ] ⊤ 待优化的控制策略 \begin{aligned} &\mathop{\min}_{u}&& \begin{aligned}J\triangleq F(x_N)+\sum_{i=0}^{N-1}L(x_{k+i|k},u_{k+i|k})\end{aligned} &&目标函数 \\ &\text{s.t.:}&& x_{k+i+1|k}=f(x_{k+i|k},u_{k+i|k}) &&系统模型\\ &&&x_{k+i|k}\in\mathcal{X}&&状态约束\\ &&&u_{k+i|k}\in\mathcal{U}&&控制约束\\ &&& x_{k|k}=x_{k}&&当前系统状态\\ &&& u = \left [ u_{k|k},\dots,u_{k+i|k},\dots,u_{k+N-1|k} \right ] ^\top&&待优化的控制策略 \end{aligned} minus.t.:J≜F(xN)+i=0∑N−1L(xk+i∣k,uk+i∣k)xk+i+1∣k=f(xk+i∣k,uk+i∣k)xk+i∣k∈Xuk+i∣k∈Uxk∣k=xku=[uk∣k,…,uk+i∣k,…,uk+N−1∣k]⊤目标函数系统模型状态约束控制约束当前系统状态待优化的控制策略
二、无约束线性模型预测控制
当系统模型为线性,即 x k + 1 = A x k + B u k x_{k+1}=Ax_{k}+Bu_{k} xk+1=Axk+Buk, 且无状态约束和控制约束的模型预测控制为无约束线性模型预测控制。
1. 无约束线性模型预测控制问题-----标准型
标准式 P1:
min U ˉ J ≜ F ( x N ) + ∑ i = 0 N − 1 L ( x k + i ∣ k , u k + i ∣ k ) 目标函数 s.t.: x k + i + 1 ∣ k = A x k + i ∣ k + B u k + i ∣ k 系统模型 x k ∣ k = x k 当前系统状态 U ˉ = [ u k ∣ k , … , u k + i ∣ k , … , u k + N − 1 ∣ k ] ⊤ 待优化的控制策略 \begin{aligned} &\mathop{\min}_{\bar U}&& \begin{aligned}J\triangleq F(x_N)+\sum_{i=0}^{N-1}L(x_{k+i|k},u_{k+i|k})\end{aligned} &&目标函数 \\ &\text{s.t.:}&& x_{k+i+1|k}=Ax_{k+i|k}+Bu_{k+i|k} &&系统模型\\ &&& x_{k|k}=x_{k}&&当前系统状态\\ &&& \bar U = \left [ u_{k|k},\dots,u_{k+i|k},\dots,u_{k+N-1|k} \right ] ^\top&&待优化的控制策略 \end{aligned} minUˉs.t.:J≜F(xN)+i=0∑N−1L(xk+i∣k,uk+i∣k)xk+i+1∣k=Axk+i∣k+Buk+i∣kxk∣k=xkUˉ=[uk∣k,…,uk+i∣k,…,uk+N−1∣k]⊤目标函数系统模型当前系统状态待优化的控制策略
这里目标函数通常选为 J ≜ x k + N ∣ k ⊤ Q N x k + N ∣ k + ∑ i = 0 N − 1 ( x k + i ∣ k ⊤ Q x k + i ∣ k + u k + i ∣ k ⊤ R u k + i ∣ k ) J\triangleq x_{k+N|k}^\top{Q}_Nx_{k+N|k}+\sum_{i=0}^{N-1}\left(x_{k+i|k}^\top{Q}x_{k+i|k}+u_{k+i|k}^\top{R}u_{k+i|k}\right) J≜xk+N∣k⊤QNxk+N∣k+∑i=0N−1(xk+i∣k⊤Qxk+i∣k+uk+i∣k⊤Ruk+i∣k), 跟踪目标为系统原点; x k + N ∣ k ⊤ Q N x k + N ∣ k x_{k+N|k}^\top{Q}_Nx_{k+N|k} xk+N∣k⊤QNxk+N∣k终端误差指标,确保系统稳定性; x k + i ∣ k ⊤ Q x k + i ∣ k x_{k+i|k}^\top{Q}x_{k+i|k} xk+i∣k⊤Qxk+i∣k 误差积分指标,越小表示误差积分越小; u k + i ∣ k ⊤ R u k + i ∣ k u_{k+i|k}^\top{R}u_{k+i|k} uk+i∣k⊤Ruk+i∣k对控制量的指标,越小代表能量消耗越少;这里跟踪目标为系统原点。
2. 无约束线性模型预测控制问题-----紧凑型
1、动态方程转换
a) 根据系统的状态方程 x k + i + 1 ∣ k = A x k + i ∣ k + B u k + i ∣ k x_{k+i+1|k}=Ax_{k+i|k}+Bu_{k+i|k} xk+i+1∣k=Axk+i∣k+Buk+i∣k以及初值 x k ∣ k = x k x_{k|k}=x_{k} xk∣k=xk,递归推导得
x k + 1 ∣ k = A x k ∣ k + B u k ∣ k x k + 2 ∣ k = A x k + 1 ∣ k + B u k + 1 ∣ k = A 2 x k ∣ k + A B u k ∣ k + B u k + 1 … x k + N ∣ k = A x k + N − 1 ∣ k + B u k + N − 1 = A N x k + A N − 1 B u k + … … + A B u k + N − 2 + B u k + N − 1 \begin{aligned}&{x_{k+1|k}=Ax_{k|k}+Bu_{k|k}}\\ &{x_{k+2|k}=Ax_{k+1|k}+Bu_{k+1|k}=A^2x_{k|k}+ABu_{k|k}+Bu_{k+1}}\\ &\dots\\ &x_{k+N|k}={Ax_{k+N-1|k}+Bu_{k+N_-1}=A^{N}x_k+A^{N-1}Bu_k+\ldots\ldots+ABu_{k+N-2}+Bu_{k+N-1}}\end{aligned} xk+1∣k=Axk∣k+Buk∣kxk+2∣k=Axk+1∣k+Buk+1∣k=A2xk∣k+ABuk∣k+Buk+1…xk+N∣k=Axk+N−1∣k+Buk+N−1=ANxk+AN−1Buk+……+ABuk+N−2+Buk+N−1
b) 上述方程可以重写为以下紧凑形式
[ x k ∣ k x k + 1 ∣ k x k + 2 ∣ k ⋯ x k + N ∣ k ] ⏟ X ˉ = [ I A A 2 ⋯ A N ] ⏟ A ˉ x k + [ 0 0 . . . 0 B 0 . . . 0 A B B . . . 0 ⋯ . . . . . . . . . A N − 1 B A N − 2 B . . . B ] ⏟ B ˉ [ u k u k + 1 ⋯ ⋯ u k + N − 1 ] ⏟ U ˉ \underbrace{\begin{bmatrix}{x_{k|k}}\\{x_{k+1|k}}\\{x_{k+2|k}}\\\cdots\\{x_{k+N|k}}\end{bmatrix}}_{\bar{{X}}}=\underbrace{\begin{bmatrix}{I}\\{A}\\{A^2}\\\cdots\\A^{N}\end{bmatrix}}_{\bar{A}}{x_k}+\underbrace{\begin{bmatrix}{0}&0&...&0\\{B}&0&...&0\\{AB}&{B}&...&0\\\cdots&...&...&...\\{A^{N-1B}}&{A^{N-2}B}&...&{B}\end{bmatrix}}_{\bar B}\underbrace{\begin{bmatrix}{u_k}\\{u_{k+1}}\\\cdots\\\cdots\\{u_{k+N-1}}\end{bmatrix}}_{\bar U} Xˉ xk∣kxk+1∣kxk+2∣k⋯xk+N∣k =Aˉ IAA2⋯AN xk+Bˉ 0BAB⋯AN−1B00B...AN−2B...............000...B Uˉ ukuk+1⋯⋯uk+N−1
即:
X ˉ = A ˉ x k + B ˉ U ˉ \begin{align} {\bar X} = {\bar A}x_{k}+ {\bar B} {\bar U} \end{align} Xˉ=Aˉxk+BˉUˉ
2. 目标函数转换
J = X ˉ ⊤ [ Q ⋱ Q Q N ] ⏟ Q ˉ ( N + 1 ) × ( N + 1 ) X ˉ + U ˉ ⊤ [ R ⋱ R ] ⏟ R ˉ N × N U ˉ = X ˉ ⊤ Q ˉ X ˉ + U ˉ ⊤ R ˉ U ˉ \begin{align} J =& {\bar X}^\top\underbrace{\begin{bmatrix} Q& & & \\ & \ddots & & \\ & & Q& \\ & & &Q_N \end{bmatrix} }_{\bar Q_{(N+1) \times (N+1)}}{\bar X}+{\bar U}^\top\underbrace{\begin{bmatrix} R& & \\ & \ddots& \\ & &R \end{bmatrix}}_{\bar R_{N\times N}} {\bar U} \notag\\ =& {\bar X}^\top{\bar Q}{\bar X}+{\bar U}^\top{\bar R}{\bar U} \end{align} J==Xˉ⊤Qˉ(N+1)×(N+1) Q⋱QQN Xˉ+Uˉ⊤RˉN×N R⋱R UˉXˉ⊤QˉXˉ+Uˉ⊤RˉUˉ
根据标准式 P1,(1)和(2),可以得到无约束线性模型预测控制问题----紧凑型:
min U ˉ J = 1 2 U ˉ ⊤ H U ˉ + f ⊤ U ˉ + c 目标函数 s.t.: X ˉ = A ˉ x k + B ˉ U ˉ 系统模型 U ˉ = [ u k ∣ k , … , u k + i ∣ k , … , u k + N − 1 ∣ k ] ⊤ 待优化的控制策略 \begin{aligned} &\mathop{\min}_{\bar U}&& \begin{aligned}J=\frac{1}{2}{\bar U}^\top H{\bar U}+{f^\top}{\bar U}+c\end{aligned} &&目标函数 \\ &\text{s.t.:}&&{\bar X} = {\bar A}x_{k}+ {\bar B} {\bar U} &&系统模型\\ &&& \bar U = \left [ u_{k|k},\dots,u_{k+i|k},\dots,u_{k+N-1|k} \right ] ^\top&&待优化的控制策略 \end{aligned} minUˉs.t.:J=21Uˉ⊤HUˉ+f⊤Uˉ+cXˉ=Aˉxk+BˉUˉUˉ=[uk∣k,…,uk+i∣k,…,uk+N−1∣k]⊤目标函数系统模型待优化的控制策略
3. 无约束线性模型预测控制问题-----解析解
将等式约束(1)带入目标函数, 将含等式约束的QP问题转换为无约束的QP问题
J = X ˉ ⊤ Q ˉ X ˉ + U ˉ ⊤ R ˉ U ˉ = x k ⊤ A ˉ ⊤ Q ˉ A ˉ x k + 2 x k ⊤ A ˉ ⊤ Q ˉ B ˉ U ˉ + U ˉ ⊤ B ˉ ⊤ Q ˉ B ˉ U ˉ + U ˉ ⊤ R ˉ U ˉ = 1 2 U ˉ ⊤ 2 ( B ˉ ⊤ Q ˉ B ˉ + R ˉ ) ⏟ H U ˉ + 2 x k ⊤ A ˉ ⊤ Q ˉ B ˉ ⏟ f ⊤ U ˉ + x k ⊤ A ˉ ⊤ Q ˉ A ˉ x k ⏟ c = 1 2 U ˉ ⊤ H U ˉ + f ⊤ U ˉ + c \begin{align} J =& {\bar X}^\top{\bar Q}{\bar X}+{\bar U}^\top{\bar R}{\bar U}\notag\\ =&{x}_k^\top{\bar A}^\top{\bar Q}{\bar A}{x}_k+2{x}_k^\top{\bar A}^\top{\bar Q}{\bar B}{\bar U}+{\bar U}^\top{\bar B}^\top{\bar Q}{\bar B}{\bar U}+{\bar U}^\top{\bar R}{\bar U}\notag\\ =&\frac{1}{2}{\bar U}^\top \underbrace{2\left({\bar B}^\top{\bar Q}{\bar B}+{\bar R}\right)}_{H} {\bar U}+ \underbrace{2{x}_k^\top{\bar A}^\top{\bar Q}{\bar B}}_{f^\top}{\bar U}+ \underbrace{{x}_k^\top{\bar A}^\top{\bar Q}{\bar A}{x}_k}_{c}\notag\\ =&\frac{1}{2}{\bar U}^\top H{\bar U}+{f^\top}{\bar U}+c\notag \end{align} J====Xˉ⊤QˉXˉ+Uˉ⊤RˉUˉxk⊤Aˉ⊤QˉAˉxk+2xk⊤Aˉ⊤QˉBˉUˉ+Uˉ⊤Bˉ⊤QˉBˉUˉ+Uˉ⊤RˉUˉ21Uˉ⊤H 2(Bˉ⊤QˉBˉ+Rˉ)Uˉ+f⊤ 2xk⊤Aˉ⊤QˉBˉUˉ+c xk⊤Aˉ⊤QˉAˉxk21Uˉ⊤HUˉ+f⊤Uˉ+c
其中
H = 2 ( B ˉ ⊤ Q ˉ B ˉ + R ˉ ) , f = B ˉ ⊤ Q ˉ A ˉ x k = G x k H=2\left({\bar B}^\top{\bar Q}{\bar B}+{\bar R}\right),f={\bar B}^\top{\bar Q}{\bar A}{x}_k=G{x}_k H=2(Bˉ⊤QˉBˉ+Rˉ),f=Bˉ⊤QˉAˉxk=Gxk
根据函数的极值条件, U ˉ ∗ {\bar U}^* Uˉ∗为 ∇ J ( U ˉ ∗ ) = 0 \nabla{J}({\bar U}*)=0 ∇J(Uˉ∗)=0;目标函数为二次函数(凸函数), U ˉ ∗ {\bar U}^* Uˉ∗为最优解。
根据目标函数 J J J的表达式以及极值条件,我们得出 无约束线性模型预测控制问题-----解析解
U ˉ ∗ = − H − 1 f = − H − 1 G x k {\bar U}^* =- H^{-1}f=- H^{-1}G{x}_k Uˉ∗=−H−1f=−H−1Gxk
4. MATLAB 代码示例
代码如下(示例):
clear; clc; close all;
% 线性系统系数矩阵
A=[1 0 1 0; 0 1 0 1;0 0 1 0; 0 0 0 1];
B=[0 0;0 0;1 0;0 1];
% 初始状态量-如果不能在下一步回到约束范围内,则会造成无解
x0=[8; -4; -0.2;-0.1];
% 预测步长
N=5;
% 优化目标参数,加权矩阵
Q=[10 0 0 0;0 20 0 0; 0 0 100 0 ;0 0 0 100 ];
R=eye(size(B,2));% 紧凑形式矩阵
At=zeros(size(A,1)*N,size(A,1));
Bt = zeros(size(A,1)*N,size(B,2)*N);
for i=1:1:NAt(size(A,1)*(i-1)+1:size(A,1)*i,:) = A^i;for j=1:1:iBt(size(A,1)*(i-1)+1:size(A,1)*i,size(B,2)*(j-1)+1:size(B,2)*j)=A^(i-j)*B;end
endQ_bar = kron(eye(N),Q);
R_bar = kron(eye(N),R);H=2*(Bt'*Q_bar*Bt + R_bar);
G = Bt'*Q_bar*At;%初始值
x=x0;
xk=x0;for k=1:100%最优解U = -H\G*xk;% 采用优化得到的控制量的第一个元素作为实际作用的控制量,代入到原系统中得到下一个时刻的状态量u(:,k) = U(1:size(B,2));%动态方程更新x(:, k+1) = A*x(:, k) + B*u(:,k);xk = x(:, k+1);
end%状态图
figure('Color','w');
plot(x(1,:),'c-','LineWidth',1.5);hold on
plot(x(2,:),'g-','LineWidth',1.5);hold on
plot(x(3,:),'b-','LineWidth',1.5);hold on
plot(x(4,:),'m-','LineWidth',1.5);hold on
legend('$x_1$','$x_2$','$x_3$','$x_4$','Interpreter','latex');
set(gca,'FontSize',20,'FontName','Times New Roman');%控制量图
figure('Color','w');
plot(u(1,:),'c-','LineWidth',1.5);hold on
plot(u(2,:),'g-','LineWidth',1.5);hold on
legend('$u_1$','$u_2$','Interpreter','latex');
set(gca,'FontSize',20,'FontName','Times New Roman');
这篇关于简单入门--无约束线性模型预测控制的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







