本文主要是介绍运筹说 第98期|无约束极值问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
上一期我们一起学习了关于非线性规划问题的一维搜索方法的相关内容,本期小编将带大家学习非线性规划的无约束极值问题。
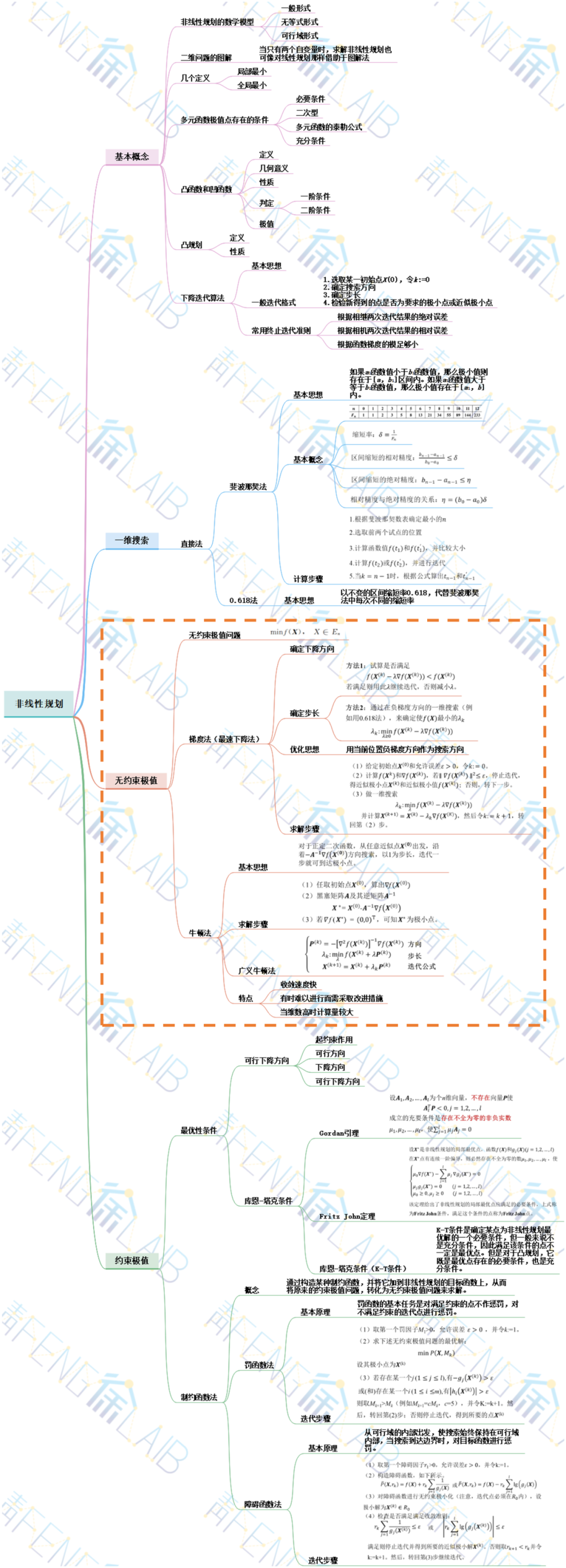
下面,让我们从实际问题出发,学习无约束极值问题吧!
一、问题描述及求解原理
1 无约束极值问题的定义
无约束极值问题可表述为
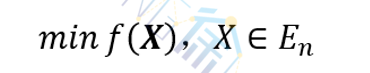
在求解上述问题时常使用迭代法。
2 迭代法
迭代法的基本思想:在一个近似点处选定一个有利搜索方向,沿这个方向进行一维寻查,得出新的近似点。然后对新点施行同样手续,如此反复迭代,直到满足预定的精度要求为止。根据搜索方向的取法不同,可以有各种算法。
迭代法的分类
(1)解析法
要用到函数的一阶导数和(或)二阶导数,由于用到了函数的解析性质,故称为解析法;
(2)直接法
在迭代过程中仅用到函数值,而不要求函数的解析性质,这类方法称为直接法。
一般说来,直接法的收敛速度较慢,只是在变量较少时才适用。但直接法的迭代步骤简单,特别是当目标函数的解析表达式十分复杂,甚至写不出具体表达式时,它们的导数很难求得,或根本不存在,就只有用直接法了。而对于存在一阶/二阶导数且能够求导的问题来说,解析性质的收敛速度更快,下面介绍两种基本的解析法。
3 梯度法(最速下降法)
梯度法是一种古老的方法,但由于它的迭代过程简单,使用方便,而且又是理解其他非线性最优化方法的基础,所以先来说明这一方法。
确定下降方向
假定问题minf(X),X∈En 中的目标函数 f(X)具有一阶连续偏导数,它存在极小点X *。则第k+1次近似可表示为在第k次近似点X(k)上,沿方向P(k)做射线,并前进步长λ,即
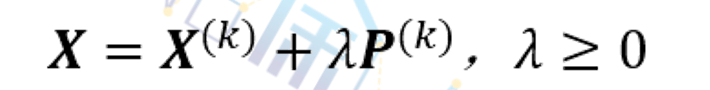
将f(X)在X(k)处作泰勒展开,得
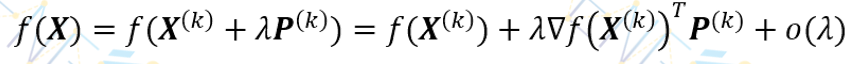
假定∇f(X(k))≠0,只要
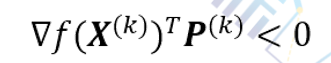
即可保证
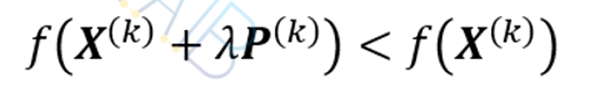
即取X(k+1)=X(k)+λP(k),就能改善目标函数值。此时,只要使∇f(X(k))TP(k)取值最小,就可求出最优的X(k+1)点。
因此,需要寻找P(k),使∇f(X(k))TP(k)最小。
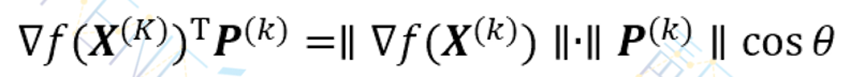
为向量∇f(X(k))T和P(k)的内积,θ为两个向量的夹角。在∥∇f(X(k))T∥和∥P(k)∥一定的情况下,显然cosθ=-1,两向量反向时,上式最小。即负梯度方向是函数值下降最快的方向。
确定步长
方法1:试算是否满足
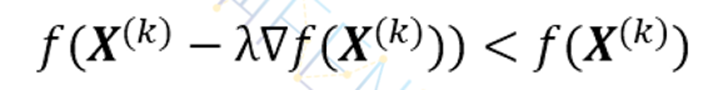
若满足则用此λ继续迭代,否则减小λ。
方法2:通过在负梯度方向的一维搜索(例如用0.618法),来确定使f(X)最小的λk
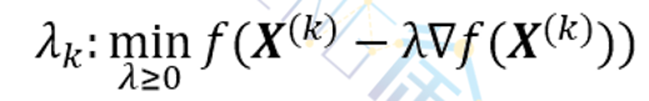
这样得到的步长称为最佳步长,有时把采用最佳步长时的梯度法成为称为最速下降法。
求解步骤
(1)给定初始点X(0)和允许误差ε>0,令k:=0。
(2)计算f(Xk)和∇f(X(k)),若∥∇f(X(k))∥2≤ε,停止迭代,得近似极小点Xk和近似极小值f(Xk);否则,转下一步。
(3)做一维搜索
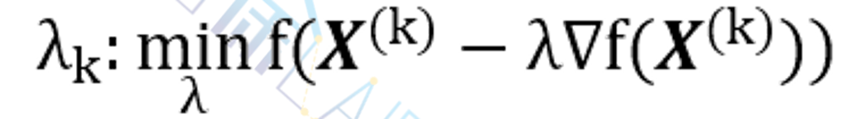
并计算X(k+1)=X(k)-λk ∇f(X(k)),然后令k:=k+1,转回第(2)步。
现设f(X)具有二阶连续偏导数,将f(X(k))-λ∇(X(k))在X(k)作泰勒展开:
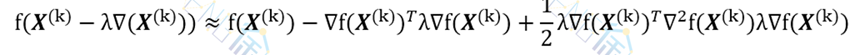
对λ求导,并令其等于零,即可得近似最佳步长的如下计算公式:
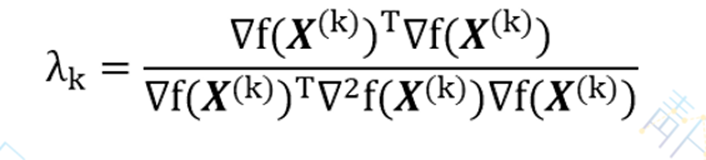
有时,把搜索方向P(k)的模格式化为1,即取
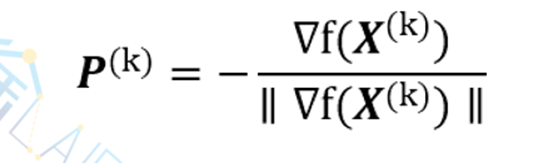
在这种情况下,f(X)=f(X(k)+λP(k))的泰勒展开为
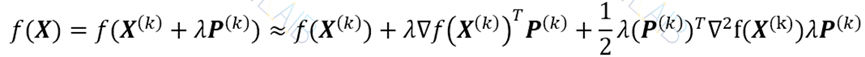
对λ求导,并令其等于零,得到
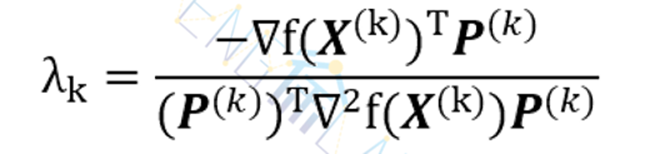
代入P(k),即近似最佳步长变为
例题求解
例题:用梯度法求函数 f(X)=x12+5x22 的极小点,取允许误差 ε=0.7
解:取初试点
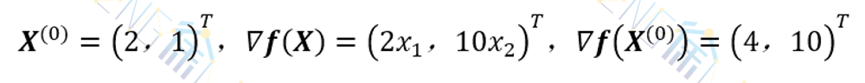
其黑塞矩阵
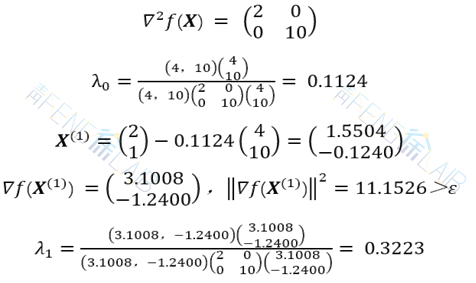
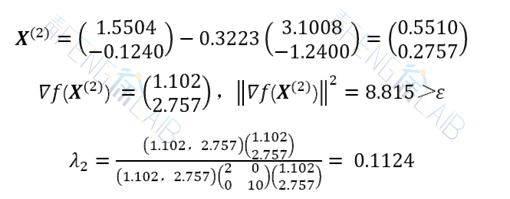
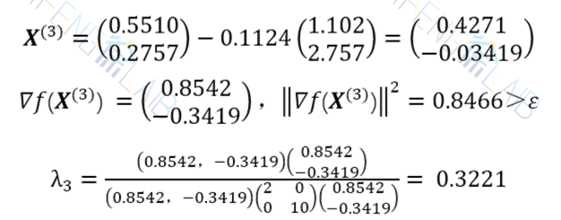
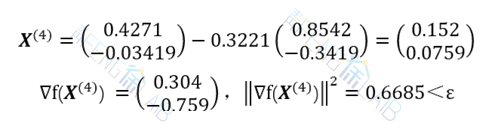
故以 X(4)=(0.152,0.0759)T为近似极小点,此时的函数值 f(X(4)) =0.0519。
该问题的精确解是X*=(0,0)T,f(X*) =0。可知,要得到真正的精确解,需无限迭代下去。
由于沿负梯度方向目标函数的最速下降性,很容易使人们误认为负梯度方向是最理想的搜索方向,最速下降法是一种理想的极小化方法。必须指出的是,某点的负梯度方向,通常只是在该点附近才具有这种最速下降的性质。在一般情况下,当用最速下降法寻找极小点时,其搜索路径呈直角锯齿状(请回忆定理3),在开头几步,目标函数值下降较快;但在接近极小点时,收敛速度常就不理想了。特别是当目标函数的等值线为比较扁平的椭圆时,收敛就更慢了。因此,在实用中常将梯度法和其他方法联合应用,在前期使用梯度法,而在接近极小点时,可改用收敛较快的其他方法。
3 牛顿法
接下来介绍另外一种基本的解析法——牛顿法。牛顿法的基本思想是利用迭代点处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似极小值。下面分别介绍正定二次函数和非正定二次函数的求解过程。
(1)正定二次函数的求解
对于正定二次函数
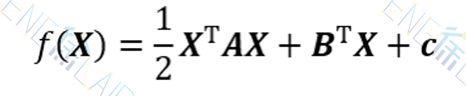
假设函数极小点为X*,则必有
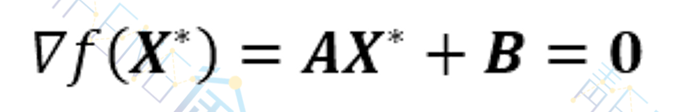
从而有AX*=-B。对任一点X(0)∈En,函数在该点得梯度
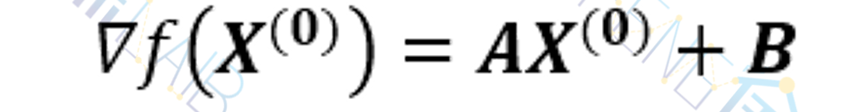
消去B,得到
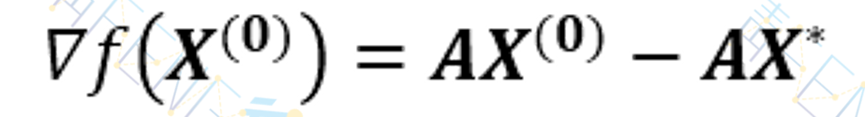
可解出
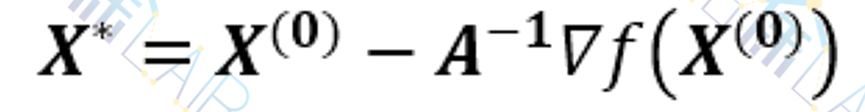
即对于正定二次函数,从任意近似点出发,沿着

方向搜索,以1为步长,迭代一步就可到达极小点。
(2)非正定二次函数的求解
对于一般n元实函数f(X),假定它有连续二阶偏导数,X(k) 为其极小点的某一近似。在这个点附近取f(X)的二阶泰勒多项式逼近:
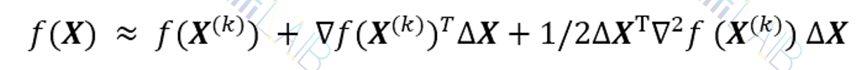
其中,∆X=X-X(k) 。
这个近似函数的极小点应满足一阶必要条件,即
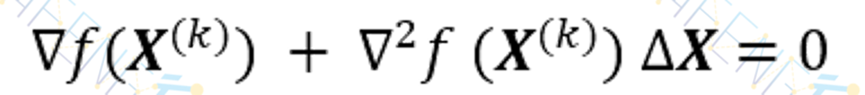
设∇2f(X(k))的逆阵存在,可得

由上式解得的该近似函数的极小点,也就仅是f(X)极小点的近似。
因此为求得f(X)的极小点,可以-[∇2 f(X(k))]-1 ∇f(X(k))为搜索方向(牛顿方向),按下述公式进行迭代:
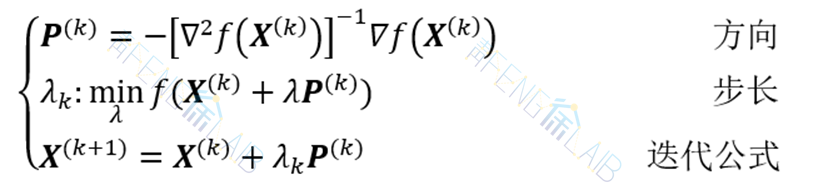
这就是阻尼牛顿法(广义牛顿法),可用于求解非正定二次函数的极小点。
例题求解
例题:用牛顿法求 f(X)=x12+5x22的极小点。
解:任取初始点X(0)=(2,1)T,算出。在本例中,
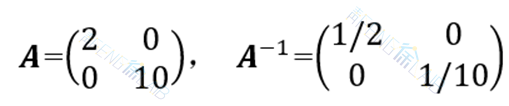
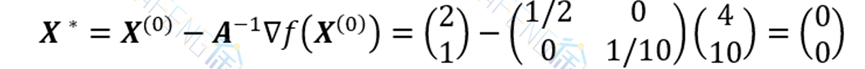
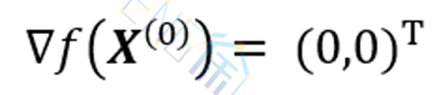
可知X* 确实为极小点。
优缺点
牛顿法的优点是收敛速度快,缺点是有时进行不下去而需采取改进措施,当维数较高时,工作量很大。
为克服梯度法收敛速度慢及牛顿法有时失效和在维数较高时计算工作量大的缺点,不少学者提出了一些更加实用的其他算法,如共轭梯度法、变尺度法等。
以上就是无约束极值问题的全部内容了,通过本节学习大家是否对该问题有了一个初步的认识呢,是否可以求解无约束极值问题呢?
作者 | 陈优 陈梦
责编 | 陈梦
审核 | 徐小峰
这篇关于运筹说 第98期|无约束极值问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






