MATLAB无约束多维极值之坐标轮换法

本文主要是介绍MATLAB无约束多维极值之坐标轮换法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、算法原理

坐标轮换法亦称变量轮换法时一种求无约束最优化问题的降维方法.其迭代过程是沿不同的坐标方向轮换地进行搜索.

例 二维极值

设初始点为x0=[1,1]，先只改变一个变量，其他变量视为常数，进行一维搜索，得到最优点x01:

x01=x0+e1*a,式中e1=[0,1]为方向,a为待求步长。通过min f(x0+e1*a)求得最优步长。

（通过进退法求得极值区间，黄金分割法求得最优步长）；

;再换一个变量，同样进行一维搜索，得到最优点x02

x02=x0+e2*a,式中e1=[1,0]为方向,a为待求步长。通过min f(x0+e2*a)求得最优步长。

（通过进退法求得极值区间，黄金分割法求得最优步长）；

;如此继续下去，直到完成一个循环，即对n个变量都轮换完毕，得到最优点x。

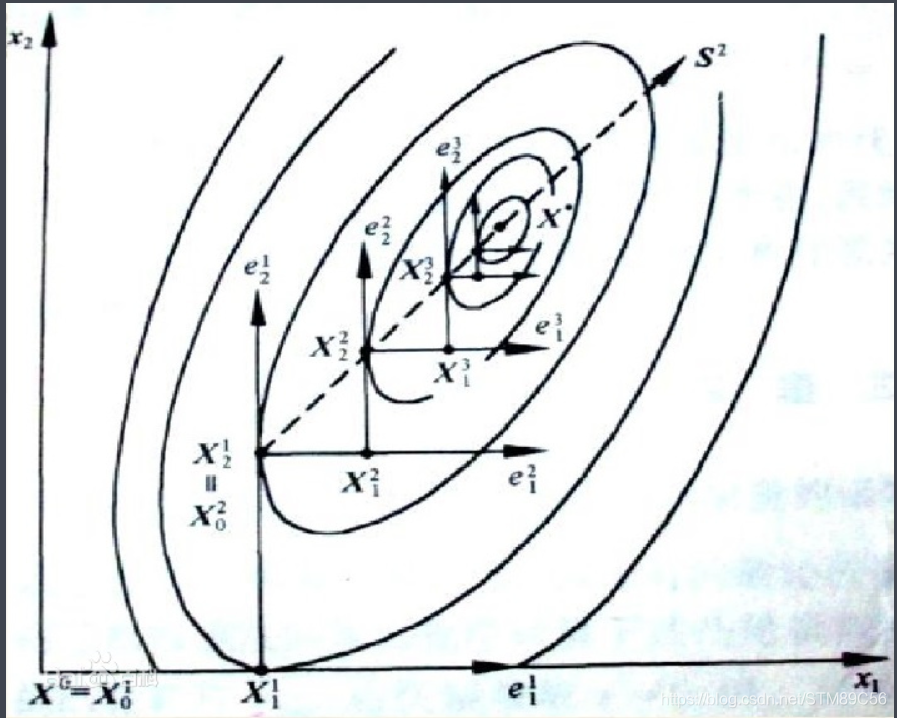
三维极值

设初始点为x0=[1,1，1]，先只改变一个变量，其他变量视为常数，进行一维搜索，得到最优点x01:

x01=x0+e1*a,式中e1=[1,0,0]为方向,a为待求步长。通过min f(x0+e1*a)求得最优步长。

（通过进退法求得极值区间，黄金分割法求得最优步长）；

;再换一个变量，同样进行一维搜索，得到最优点x02

x02=x0+e2*a,式中e1=[0,1,0]为方向,a为待求步长。通过min f(x0+e2*a)求得最优步长。

（通过进退法求得极值区间，黄金分割法求得最优步长）；

;再换一个变量，同样进行一维搜索，得到最优点x03

x03=x0+e2*a,式中e1=[0,0,1]为方向,a为待求步长。通过min f(x0+e2*a)求得最优步长。

;如此继续下去，直到完成一个循环，即对n个变量都轮换完毕，得到最优点x。

二、算法流程

三、matlab程序

%% 坐标轮换 
% syms x1 x2
f=@(x1,x2) x1.^2+x2.^2-x1*x2-10*x1-4*x2+60;
X=ZBLH(f,[0 0],1e-6,100)
function x=ZBLH(f,x0,eps,k)x0 = x0';
m = length(x0);
n = 1;
syms alfa
while n < ktemp = x0; %作为一个中间变量for i = 1:me=zeros(m,1);e(i)=1;x1 = temp + alfa*e;f_alfa=matlabFunction(eval('f(x1(1),x1(2))'));
%          d_alfa=solve(f_alfa);[~,d_alfa]=huangjin(f_alfa,0,0.1,1000);temp = temp + d_alfa*e;endx1 = temp;if norm(x0 - x1) < epsx = x1;return;endx0 = x1;
end
end
function [result,x]=huangjin(f,x0,h0,n)
tol=1e-6;
[a,b]=Min_jintui(f,x0,h0);%进退法寻找搜索区间
x1=min(a,b);
x2=max(a,b);
i=1;
while i < n%取中间值a=x1+0.382*(x2-x1);b=x1+0.618*(x2-x1);fa=f(a);fb=f(b);% 判断fa  fb大小，缩小区间if fa < fbx2=b;elsex1=a;endif  abs(x1-x2) < tolresult=f((x1+x2)/2);x=(x1+x2)/2;break;endi=i+1;
end
end
%进退法寻找搜索区间
function [a,b]=Min_jintui(f,x1,h0)
%f为函数句柄
%x1为初始点
%h0为步长
x2=x1+h0;
i=1;
if f(x2) < f(x1)x3=x2+h0;h=h0;while f(x3) < f(x2)x3=x2+h;h=i*h;i=i+1;enda=x1;b=x3;
elseTemp=x1;x1=x2;x2=Temp;h=-h0;x3=x2+h;while f(x3) < f(x2)x3=x2+h;h=i*h;i=i+1;enda=x3;b=x1;
end
end

 

这篇关于MATLAB无约束多维极值之坐标轮换法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---