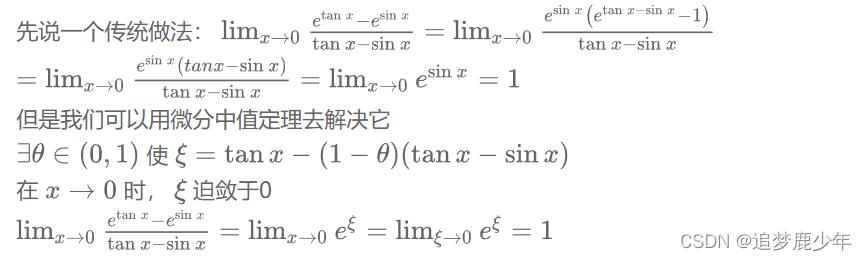微分专题
微积分直觉:隐含微分
目录 一、介绍 二、梯子问题 三、结论 四、一个额外的例子 一、介绍 让我们想象一个半径为 5 的圆,以 xy 平面为中心。现在假设我们想在点 (3,4) 处找到一条切线到圆的斜率。 好吧,为了做到这一点,我们必须非常接近圆和切线之间的空间,并沿着该曲线迈出一小步。该步骤的 y 分量为 dy,x 分量为
微分先行PID控制算法
微分先行PID控制算法 微分先行PID控制算法: 注:本文内容摘自《先进PID控制MATLAB仿真(第4版)》刘金琨 编著,研读此书受益匪浅,感谢作者! 微分先行PID控制算法: 微分先行PID控制结构,其特点是只对输出量 y ( k ) y(k) y(k)进行微分,而对给定值 y d ( k k ) y_d(kk) yd(kk)不做微分。这样,在改变给定值时,输出不会改变
不完全微分PID控制算法
不完全微分PID控制算法 注:本文内容摘自《先进PID控制MATLAB仿真(第4版)》刘金琨 编著,研读此书受益匪浅,感谢作者! 在PID控制中,微分信号的引入可改善系统的动态特性,但也容易引起高频干扰,在误差扰动突变时尤其显出微分项的不足。若在控制算法中加入低通滤波器,则可以使系统性能得到改善。 克服上述缺点的方法之一是在PID算法中加入一个一阶惯性环节(低通滤波器) G f
2.3导数与微分的基础与应用
1. 导数的基本概念 大家好,欢迎来到我们的数学大讲堂!今天我们要聊聊一个有点酷又有点恐怖的东西——导数。别担心,不是让你在黑板上画曲线的那种,而是关于“变化率”的一种数学表达。 那么,什么是导数呢?想象一下,你在开车,导数就是告诉你每一秒你的车速变化有多快。比如说,你踩了油门,车速从30公里/小时变到40公里/小时,那导数就是“哟,这小子踩油门了,车速快了!”简单来说,导数就是描述某样东西变
Python(C++)自动微分导图
🎯要点 反向传播矢量化计算方式前向传递和后向传递计算方式图节点拓扑排序一阶二阶前向和伴随模式计算二元分类中生成系数高斯噪声和特征二元二次方程有向无环计算图超平面搜索前向梯度下降算法快速傅里叶变换材料应力和切线算子GPU CUDA 神经网络算术微分 Python自动微分前向反向 自动微分不同于符号微分和数值微分。符号微分面临着将计算机程序转换为单一数学表达式的困难,并且可能导致代码效率低下
从零开始学习深度学习库-6:集成新的自动微分模块和MNIST数字分类器
在上一篇文章中,我们完成了自动微分模块的代码。深度学习库依赖于自动微分模块来处理模型训练期间的反向传播过程。然而,我们的库目前还是“手工”计算权重导数。现在我们拥有了自己的自动微分模块,接下来让我们的库使用它来执行反向传播吧! 此外,我们还将构建一个数字分类器来测试一切是否正常工作。 使用自动微分模块并非必要,不使用这个模块也没事,用原本的方法也能很好地工作。 然而,当我们开始在库中实现更复
Python(PyTorch)物理变化可微分神经算法
🎯要点 🎯使用受控物理变换序列实现可训练分层物理计算 | 🎯多模机械振荡、非线性电子振荡器和光学二次谐波生成神经算法验证 | 🎯训练输入数据,物理系统变换产生输出和可微分数字模型估计损失的梯度 | 🎯多模振荡对输入数据进行可控卷积 | 🎯物理神经算法数学表示、可微分数学模型 | 🎯MNIST和元音数据集评估算法 🍪语言内容分比 🍇PyTorch可微分优化 假设张量
直线一级倒立摆微分建模
建模内容如下: https://mp.weixin.qq.com/s?__biz=Mzg5OTIyNDEzMg==&mid=2247483673&idx=1&sn=c4e8024ebffd87611b757f7fd570f3c4&chksm=c057c632f7204f2442d0aab652847e342447fa604f04d74faafb798f022fb30e
Python烟雾液体弹性力微分模拟 | 出租车往返速度微分计算
🎯要点 🎯弹性连续力学 | 🎯弱可压缩液体 | 🎯不可压缩流体(烟雾)| 🎯高度场浅水波动 | 🎯质量弹簧系统地面碰撞 | 🎯前向欧拉方法台球刚体运动,动量和动能守恒 | 🎯高度场重建水面模型实现图像渲染器 | 🎯图像体积渲染器 | 🎯磁场模拟 🎯算法微分:Python | C++漂移扩散方程和无风险套利公式算法微分 🍇Python微分计算出租车往返速度模型 微分计
Python | C++漂移扩散方程和无风险套利公式算法微分
🎯要点 🎯漂移扩散方程计算微分 | 🎯期权无风险套利公式计算微分 | 🎯实现图结构算法微分 | 🎯实现简单正向和反向计算微分 | 🎯实现简单回归分类和生成对抗网络计算微分 | 🎯几何网格计算微分 🍇Python和C++计算微分正反向累积 算法微分在机器学习领域尤为重要。例如,它允许人们在神经网络中实现反向传播,而无需手动计算导数。 计算微分的基础是复合函数偏导数链式法则提供
华为DCN网络:微分段和业务链
1. 微分段 主要用于控制东西向流量 1.1 微分段简介 微分段(Microsegmentation),也称为基于精细分组的安全隔离,是指将数据中心网络中的服务器按照一定的原则进行分组,然后基于分组来部署流量控制策略,从而达到简化运维、安全管控的目的。 在数据中心网络中,随着数据存储以及应用的增多、网络内部流量的增大,企业面临的安全性风险也在不断增加。传统技术中可以通过划分业务子网、配
Python | C# | MATLAB 库卡机器人微分运动学 | 欧拉-拉格朗日动力学 | 混合动力控制
🎯要点 🎯正向运动学几何矩阵,Python虚拟机器人模拟动画二连杆平面机械臂 | 🎯 逆向运动学几何矩阵,Python虚拟机器人模拟动画三连杆平面机械臂 | 🎯微分运动学数学形态,Python模拟近似结果 | 🎯欧拉-拉格朗日动力学数学形态,Python模拟机器人操纵器推导的运动方程有效性 | 🎯运动规划算法,Python虚拟机器人和摄像头模拟离线运动规划算法 | 🎯移动导航卡尔曼
自动微分技术在 AI for science 中的应用
本文简记我在学习自动微分相关技术时遇到的知识点。 反向传播和自动微分 以 NN 为代表的深度学习技术展现出了强大的参数拟合能力,人们通过堆叠固定的 layer 就能轻松设计出满足要求的参数拟合器。 例如,大部分图神经网络均基于消息传递的架构。在推理阶段,用户只需给出分子坐标及原子类型,就能得到整个分子的性质。因此其整体架构与下图类似: 在模型设计阶段,我们用 pytorch 即可满足大
PID微分器与滤波器的爱恨情仇
文章目录 1 先说噪声2 噪声对于系统的影响3 对于PID控制器的影响4 加入滤波器4.1 传递函数4.2 串联微分的等效形式反馈积分 5 C语言实现6 参考 1 先说噪声 在电子设备等电路系统中,噪声是不被系统需要的电信号;电子设备产生的噪声会由于多种不同的影响而产生很大的差异。 在通信系统中,噪声是一个错误或不希望出现的随机干扰从而作用于有效的信号。 2 噪声对于系统
无偏扭曲区域采样在可微分渲染中的应用
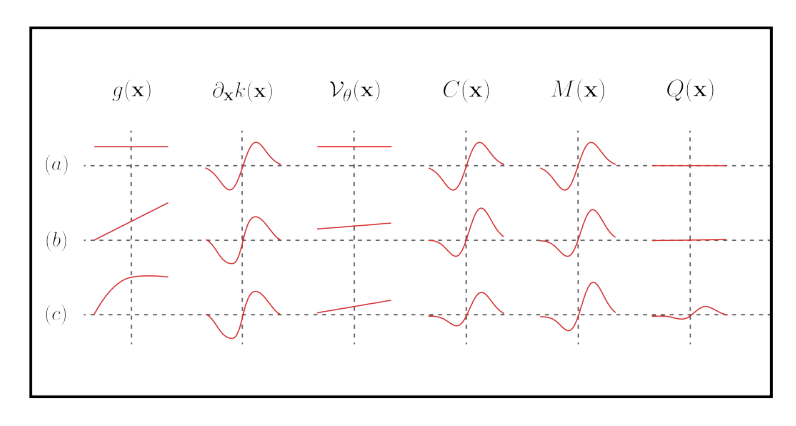
图1. 可微渲染计算光传输方程的导数。为了处理可见性的存在,最近的基于物理的可微渲染器需要显式地找到边界点[Li等人2018; Zhang等人2020],或者通过启发式方法近似边界贡献[Loubet等人2019]。我们从第一原理出发,开发了一个无偏估计器,通过内部(区域)样本计算边界贡献。我们的方法可以轻松地与现有的重要性采样方法集成,并计算准确且低方差的梯度。例如,边缘采样方法[Li等人201
Tungsten Fabric+K8s轻松上手丨通过Kubernetes网络策略进行应用程序微分段
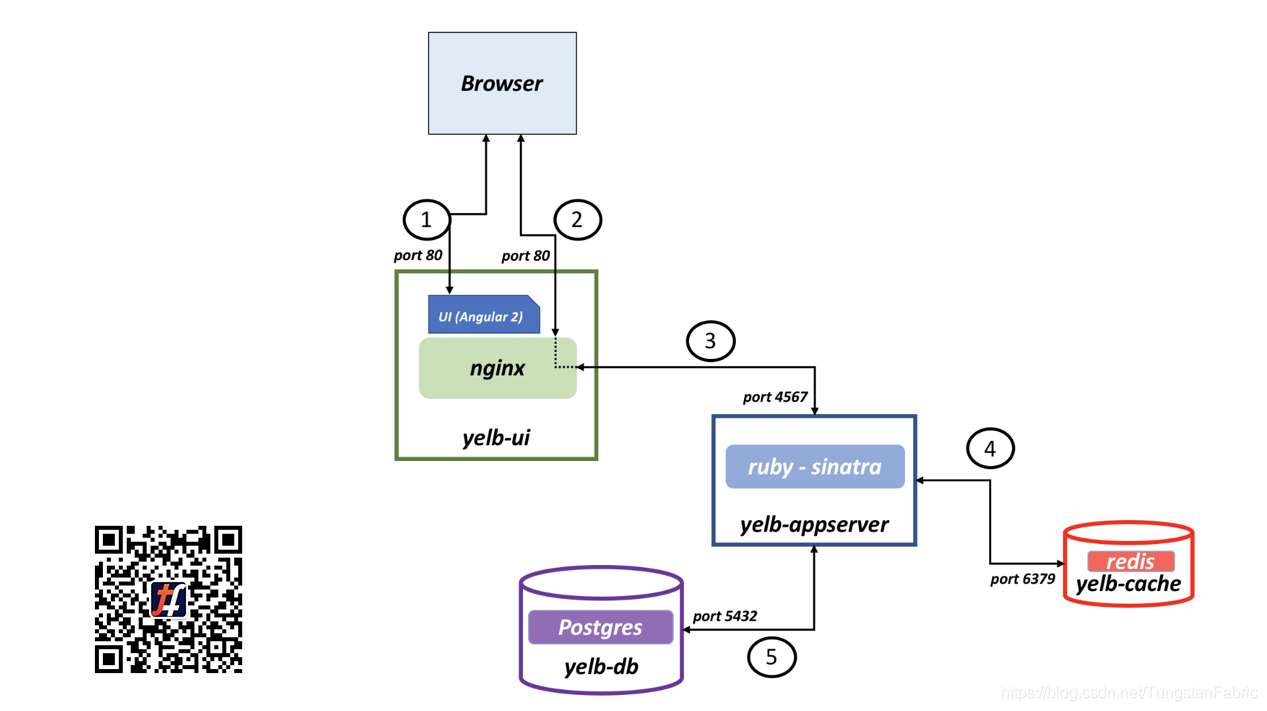
点击下载文档,查看本文所有相关链接https://tungstenfabric.org.cn/assets/uploads/files/tf-ceg-case4.pdf 在大多数生产环境中,需要实施网络访问控制。Kubernetes提供了一种方法来描述Pod 组应该如何通过使用NetworkPolicy资源进行通信。 与Kubernetes中的大多数事情一样,要使网络策略正常运行,您需要一个支
Pytorch-自动微分模块
🥇接下来我们进入到Pytorch的自动微分模块torch.autograd~ 自动微分模块是PyTorch中用于实现张量自动求导的模块。PyTorch通过torch.autograd模块提供了自动微分的功能,这对于深度学习和优化问题至关重要,因为它可以自动计算梯度,无需手动编写求导代码。torch.autograd模块的一些关键组成部分: 函数的反向传播:torch.autograd.f
请解释TensorFlow中的自动微分(Automatic Differentiation)是如何工作的。如何使用TensorFlow进行分布式训练?
请解释TensorFlow中的自动微分(Automatic Differentiation)是如何工作的。 TensorFlow中的自动微分(Automatic Differentiation)是一个强大的工具,它使得计算和优化复杂函数的梯度变得简单而高效。自动微分是TensorFlow进行深度学习模型训练的核心部分,因为梯度下降等优化算法需要知道损失函数相对于模型参数的梯度。 自动微分在Ten
高等数学基础篇之导数与微分的运算法则
导数与微分: 一、导数基本公式 二、微分基本公式 三、导数运算法则 四、微分运算法则 一、导数基本公式 二、微分基本公式 三、导数运算法则 四、微分运算法则 有理运算法则 设f(x), g(x)在x处可导,则: 复合函数运算法则 设 y=f(u)
非线性跟踪-微分器 仿真应用
非线性微分跟踪器的Matlab仿真 非线性跟踪微分器非线性跟踪微分器的一般形式 MATLAB仿真离散微分跟踪器的MATLAB仿真仿真 r = 50 T=0.01仿真 r = 10 T=0.01仿真 r = 100 T=0.01 对阶跃信号 10u(t-5)的仿真简单结论 非线性跟踪微分器 实际工程问题中,测量信号经常不连续或者带随机噪声,需要提取连续信号和微分信号。比如PID调
理解深度学习中的自动微分
一、自动微分定义 引用自 李沐《动手学深度学习》 深度学习框架可以通过自动计算导数,即自动微分(automatic differentiation)来加快求导。具体的,根据设计好的模型,torch会构建一个计算图(computational graph), 来跟踪计算是哪些数据通过哪些操作组合起来产生输出。 自动微分使系统能够随后反向传播梯度。 这里,反向传播(back propagate)意
从零开始学习深度学习库-4:自动微分
欢迎来到本系列的第四部分,在这里我们将讨论自动微分 介绍 自动微分(Automatic Differentiation,简称AD)是一种计算数学函数导数(梯度)的技术。在深度学习和其他领域中,自动微分是一种极其重要的工具,特别是在梯度下降这类优化算法中。不同于数值微分和符号微分,自动微分以一种高效和精确的方式计算导数。 自动微分的关键特点包括: 1.计算图: 自动微分通常通过构建一个计算图
自动微分运算TORCH.AUTOGRAD
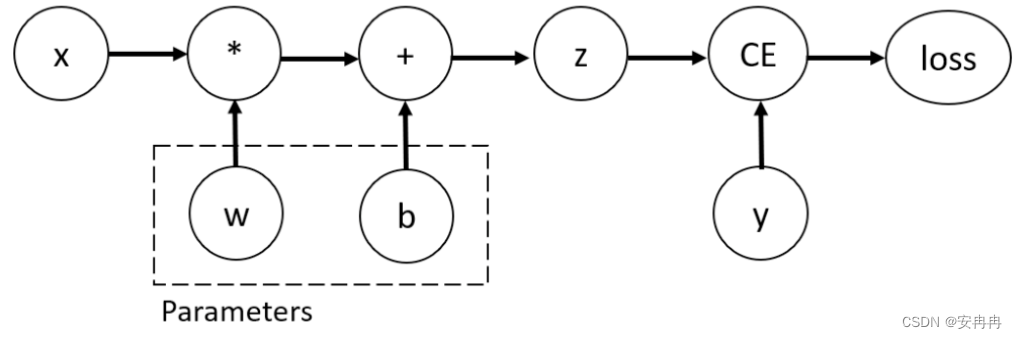
Tensor、函数和计算图 反向传播算法中,模型参数根据相对于每个给定参数的损失函数的梯度来调整。 为了计算这些梯度,PyTorch 有一个内置的微分运算引擎叫 torch.autograd。它支持对任何计算图自动计算梯度。 考虑一个最简单的单层神经网络,它有输入值 x、参数 w 和 b、和一些损失函数。它可以在 PyTorch 中这么定义: import torchx = torch.
考研数二第十三讲 从洛必达法则说起—微分中值定理在极限中的简单应用
我们之前介绍极限的文章当中讲过一道例题: 在这题当中,由于x趋向于0的时候,sinx和x都趋向于0,我们要计算0除以0的结果,当时为了解决这个问题,我们用上了夹逼法,对它进行了缩放之后才得到了极限。类似的极限还有很多,本质上来说问题在于当分子和分母都趋向于0时,我们很难计算得到结果。 洛必达 洛必达变形 但是关于洛必达法则使用的限制看起来有些麻烦,其实我们只需要牢记两点