理解深度学习中的自动微分

一、自动微分定义

引用自 李沐《动手学深度学习》
深度学习框架可以通过自动计算导数，即自动微分（automatic differentiation）来加快求导。具体的，根据设计好的模型，torch会构建一个计算图（computational graph）， 来跟踪计算是哪些数据通过哪些操作组合起来产生输出。 自动微分使系统能够随后反向传播梯度。 这里，反向传播（back propagate）意味着跟踪整个计算图，填充关于每个参数的偏导数。

以上这段话总体介绍了自动微分的定义及其各类概念，我们将在下面的讲解中进行不断的分点理解。

阅读以下内容时博主在这里斗胆将自动微分与反向传播画上等号，即以下文章中，反向传播与自动微分意义相等。

二、反向传播中的概念

1. 计算图（dynamic graph）

上来先入为主，PyTorch在进行反向传播时是通过图的形式进行计算的，这个图称为计算图。这句话的意思是，反向传播这一个过程不是凭空产生的说传播就传播，而是借助图来传播的，这图叫计算图。
下图即是一个简单的计算图，其中蓝色代表叶子节点，绿色代表根节点，灰色代表要进行的运算，箭头方向为前向传播的方向。

初看这张图时可能有很多疑问，什么是叶子节点，什么又是运算，什么是前向传播，标题中的反向传播又是什么。不要担心，相信你阅读完这篇文章后都会明白的。

首先，在pytorch的计算图里只有两种东西：数据（tensor） 和 运算（operation），其中：

• 运算包括了：加减乘除、开方、幂指对、三角函数等可求导运算
• 数据包括了：叶子节点 和 非叶子节点 两种数据类型（所以数据就是节点，节点就是数据），其中，数据为Tensor（张量）格式。每个Tensor（每个节点、每个数据）都具有如下属性：

1. 是否可以（需要）求（计算）梯度 ：.requires_grad

2. 创建出（运算出）该节点的方式：.grad_fn

3. 是否为叶子节点 ：.is_leaf

4. 梯度值：.grad

也就是说，计算图中的每个节点（数据）都有四个属性围绕着他，这四个属性存储了这个数据的一些基本信息，可以表明这个节点的身份信息，同时也决定了它是否是我们反向传播的最终目标（后续会讲）。
既然我们已经知道了计算图的组织结构，即 数据 + 运算，而且我们也知道了数据分两种，分别是叶子节点和非叶子节点，那我们怎么来判断某个数据是否是叶子节点呢？

2. 是否是叶子节点

我们判断计算图中的数据是否是叶子节点时，我们是有判断规律的。
两种情况下的tensor会是叶子节点：

1. 它的属性 .requires_grad为False
   也就是说，当一个张量的 requires_grad= False，那它就是叶子节点。

X = torch.tensor([1.0, 2.0, 3.0]) #没有手动指明requires_grad=True，则默认为False
print(X.requires_grad)
print(X.is_leaf)>>>False #不可求梯度
>>>True #是叶子节点

2. 它的属性 .requires_grad为True，但不是经由运算得到的。
   也就是说，当一个张量时的 requires_grad=True，并且此该张量是由用户自定义出来的，而不是经过运算得到，它是叶子节点。

X = torch.tensor([1.0, 2.0, 3.0], requires_grad=True) #手动指明requires_grad=True
print(X.requires_grad)
print(X.is_leaf)>>>True #可求梯度
>>>True #是叶子节点

等一下等一下，我知道你们有点迷，因为我也迷了，我们捋一捋：

假如一个张量的requires_grad为False，它一定是叶子节点，也就是说，不管你是定义出来的张量，还是通过运算得出来的张量，只要你的requires_grad为False，那你就是叶子节点。我们来拿代码看一下：

x = torch.tensor([1.0, 2.0, 3.0]) #定义出来的张量x，默认requires_grad为False
y = torch.tensor([1.0, 2.0, 3.0]) #定义出来的张量y，默认requires_grad为False
z1 = x + 1    #通过x+1运算出来的张量z1，requires_grad为False
z2 = torch.mul(x, y)  #通过x*y运算出来的张量z2，requires_grad为False
print(z1)
print(z2)
#验证他们的属性
print(x.requires_grad, x.is_leaf)
print(y.requires_grad, y.is_leaf)
print(z1.requires_grad, z1.is_leaf)
print(z2.requires_grad, z2.is_leaf)>>>tensor([2., 3., 4.])
>>>tensor([1., 4., 9.])
>>>False True
>>>False True
>>>False True
>>>False True

我们发现，只要是requires_grad=False的Tensor，它都是叶子节点。

看到这里可能有一部分人有疑问了，既然我们自定义的x和y的requires_grad是默认为False的，那对他们进行运算得出来的z1和z2的requires_grad为啥也是False？

那么我们就引出来一个知识：如果一个张量z的形成中有requires_grad=True的张量x的参与（我们将这个requires_grad=True的张量x称作源节点），那么这个张量z的requires_grad属性也会变为True，否则为False。也就是说，既然你x（源节点）不需要计算梯度，我z是用你运算出来的，那我也不计算（我不管闲事），但如果你需要梯度计算，那我也勉强计算一下梯度吧（话是这么说，这里面是有原因的，原因就是求导的链式法则必须要求这样）。

我们来拿个代码验证一下：

x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = torch.tensor([1.0, 2.0, 3.0])
z1 = x + 1
z2 = torch.mul(x, y)
print(z1)
print(z2)
print(x.requires_grad, x.is_leaf)
print(y.requires_grad, y.is_leaf)
print(z1.requires_grad, z1.is_leaf)
print(z2.requires_grad, z2.is_leaf)>>>tensor([2., 3., 4.])
>>>tensor([1., 4., 9.])
>>>True True
>>>False True
>>>True False
>>>True False

我们只将x手动指明requires_grad=True，就发现，跟x相关的z1，z2都requires_grad=True了，但是由于z1，z2是运算而来的，他们就不是叶子节点了！

看来要不是有requires_grad=True的Tensor参与进来，将运算得出来的张量也变成可求梯度，那上面的张量就只能永远参加全是叶子节点的party了。

3. 是否可以求梯度

经过上面的对叶子节点的讲解，我们现在也大致知道了requires_grad属性是干嘛的了。当我们想要对某个tensor变量求梯度时，一定需要先保证其requires_grad属性为True（即可求梯度或者说是需要求梯度），而要保证这个tensor的requires_grad为True的话，要么你是自定义的requires_grad=True叶子节点，要么你是自定义的requires_grad=True叶子节点运算而来的非叶子节点。

这里插一嘴，指定自定义叶子节点可求梯度的方式主要有两种：

x = torch.tensor(1.).requires_grad_() # 第一种
x = torch.tensor(1., requires_grad=True) # 第二种

可以看到我们刚刚一直是使用的第二种来指定我们定义的叶子节点为可求梯度的（反正我喜欢用第二种）

好的！到此，我们即将引出我们此次文章的终极目标：求梯度！！！！！

在这里，允许我强调一点，我们的终极目标其实求的是叶子节点的梯度，虽然非叶子节点的梯度也需要求，但他们只是我们达到终极目标的垫脚石而已，不能没有，但却不那么重要。所以说，终极目标很好的解释了我为什么花了这么大的功夫去区分叶子节点和非叶子节点。

4.如何求叶子节点的梯度

我们来看一个例子，假如有以下一个式子：
$$y=(x+1)\ast (x+2)\text{\hspace{1em}(1)}$$
我们能不能想一下把其中出现过的元素（数据和运算）放到torch的计算图中，并求一下：
$$\frac{\partial y}{\partial x}\text{\hspace{1em}(2)}$$

这时我们定义的x一定是requires-grad=True了，并且我们假设x的值为2，即：

x = torch.tensor([2.0], requires_grad=True)

来画一下这个计算图吧：

我们令(x+1)为运算出来的非叶子节点a，(x+2)为运算出来的非叶子节点b，理所应当的，a、b、y也一定是requires_grad=True。

这里我们说明一下前向传播的概念：

前向传播就是将已知的叶子节点数据带入函数中顺序得出非叶子节点的结构及值的过程。也就是上图中的将x的值丢进函数里依次得出节点a、节点b、节点c的结构及值。

好家伙，这就是函数求值嘛，我小学就学过。真没错，前向传播就是函数求值，不过我们在函数求值中引入了我们计算图的概念，包括节点的结构、节点的值、运算符。

那我们不妨先用人类的思维手算一下y对x的梯度：
$$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial a}\frac{\partial a}{\partial x}+\frac{\partial y}{\partial b}\frac{\partial b}{\partial x}=(x+2)\ast 1+(x+1)\ast 1=7\text{\hspace{1em}(3)}$$
可以，这不就是 求偏导+链式法则 嘛，我们要求y对x的梯度就得先求y对a的梯度和a对x的梯度以及y对b的梯度和b对x的梯度，那我们求一下这其中出现过的梯度表达式都有哪些吧：
$$\begin{array}{rl}\frac{\partial y}{\partial a}& =\frac{\partial a\ast b}{\partial a}=b=(x+2)\\ \frac{\partial y}{\partial b}& =\frac{\partial a\ast b}{\partial b}=a=(x+1)\\ \frac{\partial a}{\partial x}& =\frac{\partial x+1}{\partial x}=1\\ \frac{\partial b}{\partial x}& =\frac{\partial x+2}{\partial x}=1\end{array}\text{\hspace{1em}(4-1)(4-2)(4-3)(4-4)}$$

既然我们的脑子可以手算出上面(4-1)到(4-4)的表达式，那么pytorch一定也可以帮我们算出来，因为函数结构是你知我知计算机也知的。

所以我们不妨假设一下，如果pytorch按照我们人脑的方式从后往前计算出梯度表达式，即依次计算出(4-1)(4-2)(4-3)(4-4)的表达式，再将这4个表达式按照(3)的链式法则一相乘，那我们需要求的y对x的梯度表达式不就出来了吗？

对于我们人来说，我们是通过眼睛来看这个函数，了解了这个函数的结构，加上我们所学的数学知识，我们方可以写出上面的求偏导表达式。

而对于pytroch，它则是使用了我们介绍过的计算图，将函数映射到计算图中，先保存最开始的叶子节点x的结构，然后不断的保存由x运算所得的非叶子节点的结构，这样对pytorch来说，根据数学知识，求每一个梯度表达式也是易如反掌啦，即：

由最后的节点开始，依次调用后向节点的表达式，分别计算(4-1)(4-2)(4-3)(4-4)的梯度表达式及其值的过程，就是反向传播！

下图计算图中绿色的部分即为pytorch计算出来的各个节点的梯度表达式：

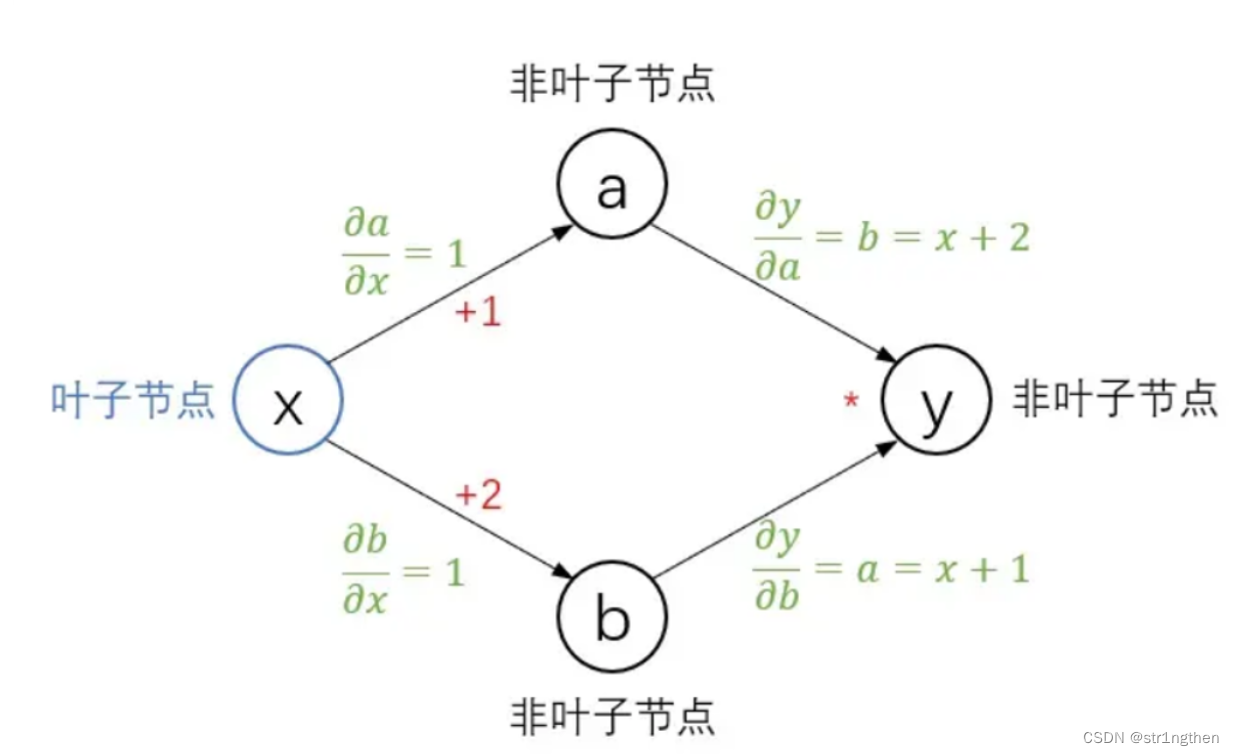
等等，等等，pytorch是怎么知道最终要求的是y对x的梯度的？我们一直在先入为主的计算y对x的梯度，认为pytorch最终计算y对x的梯度也是理所应当，那到底是什么原因能够让pytorch专门去计算y对x的梯度呢。记得我之前说过非叶子节点都是垫脚石吗？正是因为x是叶子节点，pytorch才会从最后一个节点去对它求偏导，也就是说，pytorch在一个完整的计算图中，反向传播时会对所有叶子节点求出梯度，计算图保存数据的时候同时保存了is_leaf属性信息，知道谁是叶子节点不过分吧？

所以这就是为什么 反向传播是基于计算图的，因为图这个东西是真能保存结构，真能保存运算信息，真好用啊。

以上就是自动微分的原理，其实自动微分挺简单的，无非就是你给我个函数，再给我几个requires_grad=True的源数据，我把函数转为一个数据+运算的计算图，再把源数据放到计算图的叶子节点上，根据运算自动填充后面的非叶子节点（前向传播过程）。当我填充好了之后，你要是想求源数据的梯度，我就通过最后一个节点的结构一点点去调用后方的节点结构求偏导，最后再利用一下链式法则串起来，不就求到了对叶子节点的梯度。归根到底，可以反向传播的根本原因是，通过计算图，可以在前向传播的时候保留各个节点的结构信息及过程中的运算信息。

tips：

• 我们可以将前向传播的过程看成计算图构建的过程，因为在前向传播的过程中，不断地构建出每个节点的结构和值并保存到计算图中。
• 当源数据不需要求梯度（requires_grad=False）时，由源数据运算得出的数据也不需要求梯度，因为没有保存梯度的必要了，这时，计算图也就没有存在的意义，所以计算图并不会被构建出来，所以每个数据都当叶子节点去吧。

相比于我们人类计算梯度时要列出链式法则的式子然后带入值算出结果，pytorch计算梯度非常方便，我们只需要使用反向传播函数。

5.反向传播函数

1. PyTorch提供两种求梯度的方法：backward() 和 torch.autograd.grad()
2. 这两种求梯度的区别在于前者是给叶子节点填充grad字段（导数值字段）（也就是前者可以通过 a.grad (a为叶子节点) 来获得该叶子节点的梯度值，相当于该叶子节点的grad部分被赋值了），而后者是直接返回梯度给你（后者只得出导数值而不将这个梯度存到叶子节点的grap字段中）
3. y.backward() 差不多等同于 torch.autograd.backward(y)，只有第 2) 点的区别
4. 可以看到在第二条，grad的前方都是__叶子节点__，而不是__非叶子节点__，也就是说，一般只有叶子节点才有实际意义上的grad属性（具体原因见下方）。
   下面给出在可以求导的前提下，也就是对要求梯度的tenser的requires_grad=True时，如何对其自动微分

我们通过两种自动微分方式来获得叶子节点的梯度：

1) 使用backward()

x = torch.tensor(2., requires_grad=True)a = torch.add(x, 1)
b = torch.add(x, 2)
y = torch.mul(a, b)y.backward()
print(x.grad)
>>>tensor(7.)

看一下这几个tensor的属性：

print("requires_grad: ", x.requires_grad, a.requires_grad, b.requires_grad, y.requires_grad)
print("is_leaf: ", x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)
print("grad: ", x.grad, a.grad, b.grad, y.grad)>>>requires_grad: True True True True
>>>is_leaf: True False False False
>>>grad: tensor(7.) None None None

可以看到，使用backward() 函数反向传播计算tensor的梯度时，并不保存所有tensor的梯度，而是只保存满足这几个条件的tensor的梯度：

I. 类型为叶子节点
II. requires_grad=True
III. 依赖该tensor的所有tensor的requires_grad=True。

所有满足条件的tensor梯度会自动保存到对应的grad属性里，而你需要求梯度的叶子节点一定是满足上述条件的，而计算过程中的非叶子节点的 .grad 属性默认情况下是不会被保存的，因为它们通常不是计算梯度的终点（这是torch框架的考虑设定）。

tips:

• 如果需要保存非叶子节点的grad，则可以使用a.retain_grad()，这样即可保存该非叶子节点a的grad（前提是该节点的requires_grad属性为True）。

2) 使用autograd.grad()

x = torch.tensor(2., requires_grad=True)a = torch.add(x, 1)
b = torch.add(x, 2)
y = torch.mul(a, b)grad = torch.autograd.grad(outputs=y, inputs=x)
print(grad[0])
Print(x.grad)>>>tensor(7.)
>>>None

因为指定了输出为y，输入为x，所以返回值就是 y关于x的梯度，完整的返回值其实是一个元组，保留第一个元素就行，后面元素是空白。

此外，我们发现x.grad是None，说明使用 autograd.grad() 得到的grad并不会存入x.gard中。

注意，使用 autograd.grad() 得到的是一个元组，我们只需要保留第一个元素即可，也就是grad[0]。

有任何问题请联系作者邮箱，位于作者简介处。

参考

1. https://www.bilibili.com/video/BV1yG411x7Cc/?spm_id_from=333.337.search-card.all.click&vd_source=c8e5d5163f5fc51afd4d9b45ec8c57d9
2. https://blog.csdn.net/cendrier/article/details/129045868
3. https://zhuanlan.zhihu.com/p/279758736