四十五天专题

代码随想录算法训练营第四十五天 | 115.不同的子序列，583. 两个字符串的删除操作， 72. 编辑距离

目录 115.不同的子序列思路 1.确定dp数组（dp table）以及下标的含义 2.确定递推公式 3.dp数组如何初始化 4.确定遍历顺序 5.举例推导dp数组方法一：动态规划方法二：动态规划-一维数组 583. 两个字符串的删除操作思路动态规划一 1.确定dp数组（dp table）以及下标的含义 2.确定递推公式 3.dp数组如何初始化 4.确定

代码随想录算法训练营四十五天|115.不同的子序列、583.两个字符串的删除操作、72.编辑距离

题目链接：115. 不同的子序列 - 力扣（LeetCode） class Solution(object):def numDistinct(self, s, t):""":type s: str:type t: str:rtype: int"""dp = [[0] * (len(t) + 1) for _ in range(len(s) + 1)]for i in range(len(s) +

Java重修笔记第四十五天 LinkedHashSet 类

LinkedHashSet 类 1. LinkedHashSet 是 HashSet 的子类，继承 HashSet 的方法 2. LinkedHashSet 的底层是 LinkedHashMap ，底层维护了一个数组加双向链表的组合 3. LinkedHashSet 根据元素的 hashCode 值来决定元素在 table 数组上的存储位置，同时使用链表结构来维护元素的次序（after

代码随想录算法训练营第四十五天|不同的子序列、两个字符串的删除操作、编辑距离

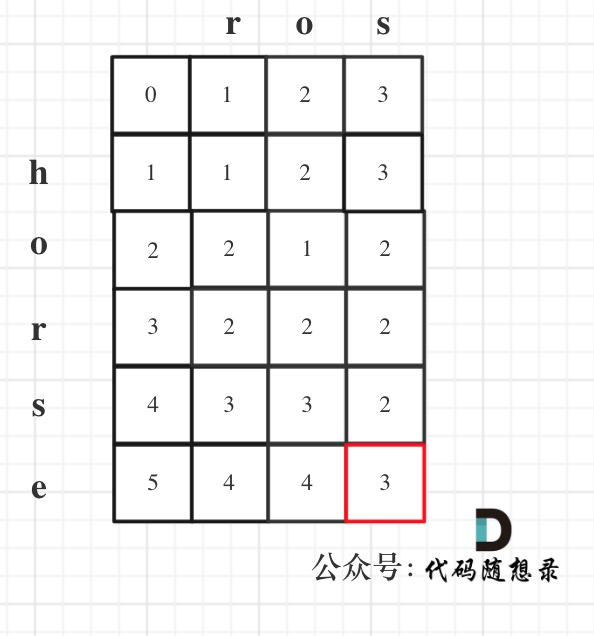
不同的子序列 leetcode 115 不要求连续。 dp数组含义：以i为尾的s中有以j为尾的t的个数为dp[i][j]。递推公式：如果s[i]==t[j]，就不需要考虑i和j这两个字母了，就等于以i-1为尾的s中有以j-1为尾的t的个数为dp[i-1][j-1]，这种情况是考虑使用i这种情况，还有不使用i的情况（例如：在bagg中找bag），此时不使用i就是以i-1为尾的s中有以j为尾的

代码随想录算法训练营第四十五天|LeetCode337 打家劫舍Ⅲ

题1：指路：337. 打家劫舍 III - 力扣（LeetCode）思路与代码：方法一：暴力暴力解法：我们讨论根结点处的偷取形式。此时情况分为两种：考虑偷取根节点，和不考虑偷取根节点。如果考虑偷取根节点时，此时我们得到的金币是根节点的值，也就是root->val，此时，因为不能连续偷取，那么再顺着往下偷取的时候就不能偷取根节点的左孩子或者右孩子，而是偷取根节点的左孩子的左孩子或者根

代码随想录算法训练营第四十五天 | 198.打家劫舍、213.打家劫舍II、337.打家劫舍 III

198.打家劫舍题目链接：https://leetcode.cn/problems/house-robber/ 文档讲解：https://www.programmercarl.com/0198.%E6%89%93%E5%AE%B6%E5%8A%AB%E8%88%8D.html 视频讲解：https://www.bilibili.com/video/BV1Te411N7SX 思路确定

【代码随想录算法训练营第四十五天|198.打家劫舍、213.打家劫舍II、337.打家劫舍III】

文章目录 198.打家劫舍213.打家劫舍II337.打家劫舍III 198.打家劫舍 dp数组在这里是抢前i个房屋的最大受益，初始化头两个dp，推导的时候从前往后推，在前一位dp和前两位dp+现在的房子的受益中找最大值。（代码随想录里给了nums=[]，的判断其实不需要，leetcode上给出nums长度大于等于1了。 class Solution:def rob(self,

第四十五天 | 322.零钱兑换

题目：322.零钱兑换尝试解答： 1.确定dp[j]含义：装满容量为j的背包所需要放的硬币个数为dp[j]; 2.动态转移方程：dp[j] = dp[j - coins[i]] + 1; 3.遍历顺序：本题应该为组合类题目，不考虑装入的顺序，只在乎硬币个数所以先物品后背包，背包容量从小到大。（错） 4.初始化：dp[0] = 1,其余均初始换为0 5.打印dp

代码随想录算法训练营第四十五天|70. 爬楼梯（进阶版），322. 零钱兑换，279.完全平方数

目录 70. 爬楼梯（进阶版）思路代码 322. 零钱兑换思路代码 279.完全平方数思路代码 70. 爬楼梯（进阶版）题目链接：57. 爬楼梯（第八期模拟笔试）文档讲解：代码随想录思路完全背包问题，物品为每次可以爬的台阶数，背包容量为所需要爬的台阶数，求装满该背包有多少种方法，而且需要考虑顺序。代码 #include <iostream>#inclu

代码随想录算法训练营第四十五天| 70. 爬楼梯（进阶），322. 零钱兑换，279.完全平方数

题目与题解 70. 爬楼梯（进阶）题目链接：70. 爬楼梯（进阶）代码随想录题解：70. 爬楼梯（进阶）解题思路：这道题要求每次可以爬1-m层的楼梯，最终爬到n，相当于完全背包问题中，有无限个重量为1-m的物品，每次可以取不同重量的物品，要求最后重量加起来等于n时有多少种排列。那这题就跟组合总和IV是一样的了，就是完全背包+排列，因此

代码随想录算法训练营第四十五天|70. 爬楼梯（进阶） 322. 零钱兑换 279.完全平方数

70. 爬楼梯（进阶）这道题目爬楼梯之前我们做过，这次再用完全背包的思路来分析一遍 https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85%E7%89%88%E6%9C%AC.html 题目大意：假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可

代码随想录算法训练营第四十五天|动态规划|70. 爬楼梯（进阶）、322. 零钱兑换、279.完全平方数

70. 爬楼梯（进阶）文章假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢？注意：给定 n 是一个正整数。输入描述：输入共一行，包含两个正整数，分别表示n, m 输出描述：输出一个整数，表示爬到楼顶的方法数。输入示例：3 2 输出示例：3 提示：当 m = 2，n = 3 时，n

华清远见作业第四十五天——FreeRTOS（第三天）

总结任务的调度算法，把实现代码再写一下抢占式调度简单来说就是谁的优先级高就先执行谁 //首先定义出任务相关信息 osThreadId-t myTask03Handle;const osThreadAttr-t myTask03-attributes={.name="myTask03",.stack-size=128*4,.priority=(osPriority-t) osPriori

代码随想录算法训练营第四十五天爬楼梯（进阶）、322. 零钱兑换、 279.完全平方数

代码随想录算法训练营第四十五天 | 爬楼梯（进阶）、322. 零钱兑换、 279.完全平方数二维爬楼梯（进阶）题目链接：题目页面 (kamacoder.com) 爬楼梯的高度n就是背包的容量每次能爬1 ~ m阶台阶，说明1 ~ m的就是物品的种类这样就把题目变成了一个完全背包问题：从1~m中任选（无线数量）求凑成n一共有多少种排列方式？ dp[0]需要初始化为 imp

训练营四十五天 | ● 70. 爬楼梯（进阶）● 322. 零钱兑换 ● 279.完全平方数

70. 爬楼梯（进阶）一次跨1-m个台阶为物品，共有n个台阶为背包容量，排列问题，完全背包代码随想录 import java.util.*; public class Main { public static void main (String[] args) { Scanner sc = new Scanner(System.in); in

代码随想录第四十五天——爬楼梯，零钱兑换，完全平方数

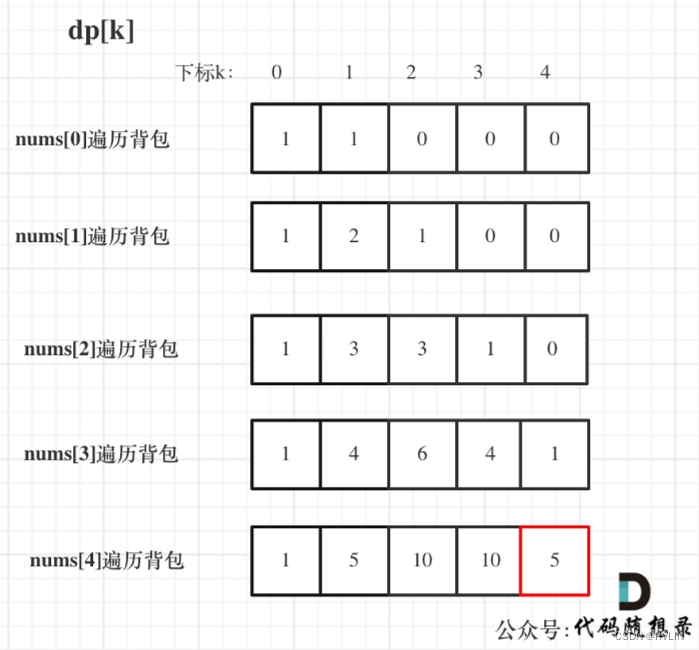
leetcode 70. 爬楼梯题目链接：爬楼梯爬楼梯也可以通过完全背包的解法求解。确定dp数组以及下标的含义 dp[i]：爬到有i个台阶的楼顶，有dp[i]种方法确定递推公式求装满背包的方法数的递推公式都是dp[i] += dp[i - nums[j]] 所以本题的递推公式：dp[i] += dp[i - j]dp数组初始化 dp[0]=1；其他初始化为0确定遍历顺序本题是背包里的

算法训练第四十五天|卡码网57. 爬楼梯、322. 零钱兑换、279.完全平方数

卡码网52. 爬楼梯：题目链接假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢？注意：给定 n 是一个正整数。输入共一行，包含两个正整数，分别表示n, m 输出一个整数，表示爬到楼顶的方法数。示例 : 输入：3 2输出：3 解答： import java.util.*;class

刷题第四十五天 1143. 最长公共子序列 1035. 不相交的线 53. 最大子数组和

class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:#dp[i][j] 以i-1 和j-1字符结尾的两个序列拥有的最长公共子序列长度#dp = [[0]*(len(text1) + 1) for _ in range(len(text2) + 1)]result = 0for i in

代码随想录算法训练营第四十五天| 70 爬楼梯 322 零钱兑换 279 完全平方数

目录 70 爬楼梯 322 零钱兑换 279 完全平方数 70 爬楼梯本题可以转化为完全背包问题进行解答。 class Solution {public:int climbStairs(int n) {vector<int>f(n + 2);f[0] = 1;int m = 2;for(int i = 1;i <= n;i++){for(int j = 1;j

代码随想录算法训练营第四十五天 _ 动态规划_ 70. 爬楼梯、322.零钱兑换、279.完全平方数、139.单词拆分。

学习目标：动态规划五部曲： ① 确定dp[i]的含义 ② 求递推公式 ③ dp数组如何初始化 ④ 确定遍历顺序 ⑤ 打印递归数组 ---- 调试引用自代码随想录！ 60天训练营打卡计划！学习内容： 70. 爬楼梯动态规划五步曲： ① 确定dp[j]的含义：容量为j的背包可以放dp[j]种排列 ② 求递推公式： dp[j] += dp[j-i]; （排列问题的标准递推公

shell学习四十五天----xargs

执行命令:xargs 当find产生一个文件列表时,该列表提供给另一个命令有时是很有用的. 案例: $touch abc.c erd.c oiy.c $ll ./erd.c ./abc.c ./oiy.c $find -name '*.c'| rm rm: 缺少操作数请尝试执行"rm --help"来获取更多信息。 $find -name '*.c'| xargs rm

代码随想录算法训练营第四十五天丨动态规划part08

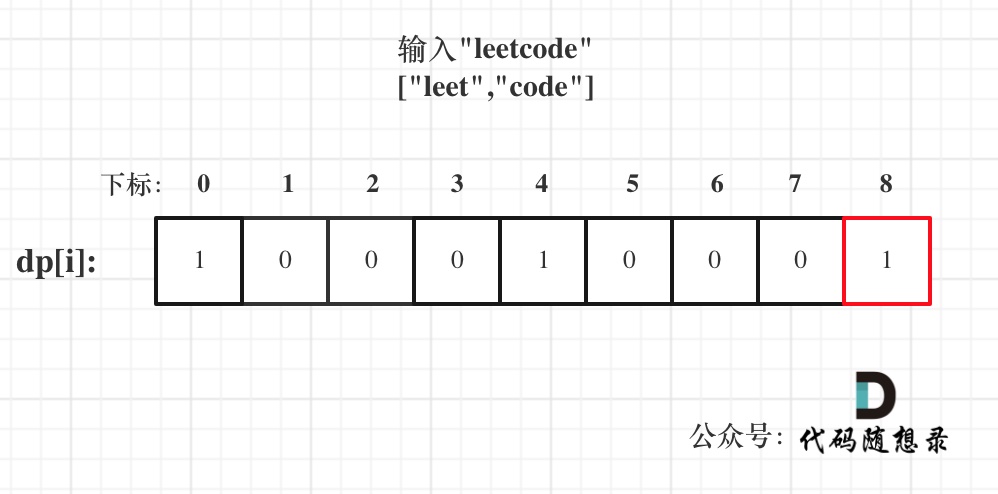
139.单词拆分思路背包问题单词就是物品，字符串s就是背包，单词能否组成字符串s，就是问物品能不能把背包装满。拆分时可以重复使用字典中的单词，说明就是一个完全背包！动规五部曲分析如下：确定dp数组以及下标的含义 dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词。确定递推公式如果确定dp[j] 是true，且 [j

代码随想录第四十五天 | 动态规划完全背包的应用：爬楼梯改编；求最小个数，循环顺序无影响（322 零钱兑换，279 完全平方数）

1、爬楼梯改编之前讲这道题目的时候，因为还没有讲背包问题，所以就只是讲了一下爬楼梯最直接的动规方法（斐波那契）改为：一步一个台阶，两个台阶，三个台阶，…，直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢 1阶，2阶，… m阶就是物品，楼顶就是背包每一阶可以重复使用，例如跳了1阶，还可以继续跳1阶，问跳到楼顶有几种方法其实就是问装满背包有几种方法。此时大家应该发现这就是一个完全背包问题了

算法随想录算法训练营第四十五天|392.判断子序列 115.不同的子序列

392.判断子序列题目：给定字符串 s 和 t ，判断 s 是否为 t 的子序列。字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。 class Solution {public boolean isSubsequence(String s, String t) {if(s

“第四十五天” 数据结构基本概念

目前看的有关数据结构的课，估计这周就看完了，但感觉差很多，还是和c一样，这样过一下吧。但可能比较急，目前是打算争取寒假回家之前把四大件都先大致过一遍。数据结构里面有很多新的定义和概念，学到现在，数据结构给我的感觉更像是，将生活中一些常用的模型抽象出来，然后用编程语言加以描述和实现对其处理，学习的也就是这个。一些感觉我已经知道的概念就不写了。

代碼隨想錄算法訓練營|第四十五天|1049. 最后一块石头的重量 II、494. 目标和、474.一和零。刷题心得（c++）

目录讀題 1049. 最后一块石头的重量 II 自己看到题目的第一想法看完代码随想录之后的想法 494. 目标和自己看到题目的第一想法看完代码随想录之后的想法 474.一和零自己看到题目的第一想法看完代码随想录之后的想法 1049. 最后一块石头的重量 II - 實作思路 Code 494. 目标和 - 實作思路 Code 474.一和零 -