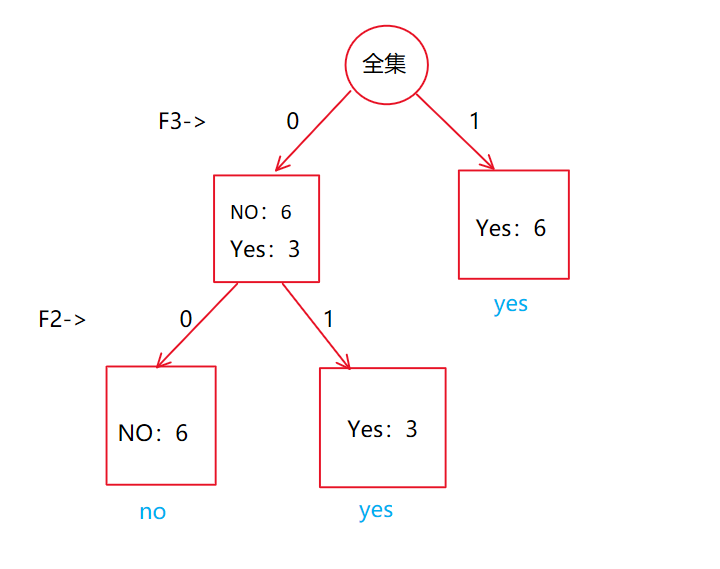
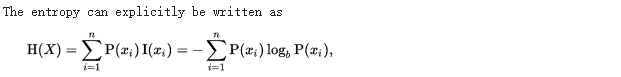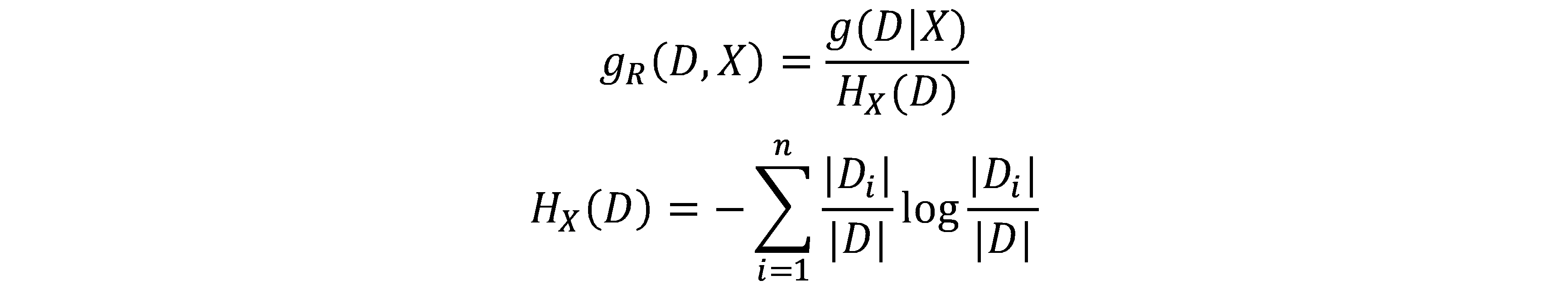id3专题

ID3算法原理及Python实践

一、ID3算法原理 ID3（Iterative Dichotomiser 3）算法是一种用于分类和预测的决策树学习算法，由Ross Quinlan在1986年提出。该算法的核心原理基于信息论中的信息增益概念，通过选择信息增益最大的属性来构建决策树。以下是ID3算法原理的详细解释： 1. 信息熵与信息增益信息熵：信息熵是度量数据集中不确定性的一个指标。在ID3算法中，信息熵用于表示数据集

手写决策树ID3算法（python）

决策数(Decision Tree)在机器学习中也是比较常见的一种算法，属于监督学习中的一种。看字面意思应该也比较容易理解，相比其他算法比如支持向量机(SVM)或神经网络，似乎决策树感觉“亲切”许多。优点：计算复杂度不高，输出结果易于理解，对中间值的缺失值不敏感，可以处理不相关特征数据。缺点：可能会产生过度匹配的问题。使用数据类型：数值型和标称型。简单介绍完毕，让我们来通过一个例子让决策

《机器学习》决策树 ID3算法

目录一、什么是决策树？ 1、概念 2、优缺点 3、核心 4、需要考虑的问题二、决策树分类标准，ID3算法 1、什么是ID3 算法 2、ID3算法怎么用 1）熵值计算公式 2）用法实例三、实操 ID3算法 1）求出play标签的熵值 2）分别计算天气、温度、湿度、风、play的信息增益 • 求outlook 总熵值及信息增益 • 求temperature 总熵值及

ID3算法详解：构建决策树的利器

目录引言 ID3算法概述算法基础信息熵编辑信息增益 ID3算法步骤决策树概念: 核心：节点 1. 根节点 2. 非叶子节点 3. 叶子节点引言在机器学习领域，决策树是一种非常流行的分类和回归方法。其中，ID3算法作为决策树算法中的经典之作，自其提出以来就备受关注。本文将详细介绍ID3算法的原理、步骤、应用以及优缺点，

AI学习指南机器学习篇-使用ID3算法构建决策树

AI学习指南机器学习篇-使用ID3算法构建决策树介绍ID3算法 ID3（Iterative Dichotomiser 3）是一种用于构建决策树的经典机器学习算法。它是由Ross Quinlan于1986年提出的，是一种基于信息论的算法，用于从一组特征中选择最佳特征来构建决策树。实现思路 ID3算法的实现思路包括以下几个关键步骤：计算数据集的熵（entropy）针对每个特征，计算该特

西瓜书总结——决策树原理+ID3决策树的模拟实现

西瓜书总结——决策树原理+ID3决策树的模拟实现前言1. 决策树结构2. 决策树的生成（注意区分属性和类别）3. 划分选择3.1 信息熵和信息增益3.2 增益率3.3 基尼指数（鸡你指数） 4. 剪枝处理4.1 预剪枝4.2 后剪枝 5. 连续值与缺失值处理5.1 连续值处理5.2 缺失值处理 6. 模拟实现ID3决策树7. ID3决策树完整代码8. 添加缺失值处理功能的ID3决策树

决策树-id3算法要点和难点具体应用

ID3（Iterative Dichotomiser 3）是一种决策树学习算法，由Ross Quinlan在1986年提出。ID3算法使用信息增益（Information Gain）作为选择划分属性的标准，旨在生成一颗决策树来对实例进行分类。下面简要介绍ID3算法的主要步骤：数据准备：确保数据集是分类问题，且特征值都是离散的。如果特征值包含缺失值或连续值，需要进行预处理（如填充缺失

论文笔记1《基于ID3决策树改进算法的客户流失预测分析》

《计算机科学》 2010年部分摘要：指出了该算法的取指偏向性以及运算效率不高等缺点，在此基础上提出了改进的ID3算法，该算法通过引入先验知识度参数，有效克服ID3算法中的取值偏向性和运算效率不高等问题。算法改进：针对传统的ID3算法的缺点与不足进行以下三点尝试性的改进。（1）引入权重因子m，设属性A有n种取值，那么m=1/n（可根据经验设定）；

ID3 到 C4.5

ID3先引用几个地址 http://blog.163.com/zhoulili1987619@126/blog/static/353082012013113083417956/

[机器学习] 第四章决策树 1.ID3(信息增益) C4.5(信息增益率) Cart(基尼指数)

参考：https://www.cnblogs.com/liuq/p/9927580.html 参考：https 文章目录一、ID3 算法信息熵🌟信息增益互信息与信息增益的关系例子优缺点停止分裂的条件Python代码二、 C4.5 算法🌟信息增益率三、Cart🌟基尼指数例子🍇 数据集的选取🍇

决策树 (Decision Tree) 原理简述及相关算法(ID3,C4.5)

Decision Tree 决策树：决策树是属于机器学习监督学习分类算法中比较简单的一种，决策树是一个预测模型；他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，而每个分叉路径则代表的某个可能的属性值，而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出，若欲有复数输出，可以建立独立的决策树以处理不同输出。下面来看个范例，就能很快理解了。

使用Python实现ID3决策树中特征选择的先后顺序，字节跳动面试真题

def empty1(pri_data): hair = [] #[‘长’, ‘短’, ‘短’, ‘长’, ‘短’, ‘短’, ‘长’, ‘长’] voice = [] #[‘粗’, ‘粗’, ‘粗’, ‘细’, ‘细’, ‘粗’, ‘粗’, ‘粗’] sex = [] #[‘男’, ‘男’, ‘男’, ‘女’, ‘女’, ‘女’, ‘女’, ‘女’] for one in pri_dat

决策树——（二）决策树的生成与剪枝ID3,C4.5

1.基本概念在正式介绍决策树的生成算法前，我们先将之前的几个概念梳理一下： 1.1 信息熵设 X X X是一个取有限个值的离散型随机变量，其分布概率为 P ( X = x i ) = p i , i = 1 , 2 , . . . , n P(X=x_i)=p_i,i=1,2,...,n P(X=xi)=pi,i=1,2,...,n 则随机变量 X X X的熵定义为 H ( X

基于ID3算法生成决策树

决策树的类型有很多，有CART、ID3和C4.5等，其中CART是基于基尼不纯度(Gini)的，而ID3和C4.5都是基于信息熵的，它们两个得到的结果都是一样的，本次定义主要针对ID3算法。在构造决策树时，第一个问题就是：当前的那个特征在划分数据是起着决定性的作用。为了找到决策性的特征必须对每个特征进行评估。因此本文针对ID3算法使用的信息熵方法划分数据的特征来进行实验。信息熵如果待分

掰开揉碎机器学习系列-决策树(1)-ID3决策树

一、决策树的理论依据： 1、熵的概念：熵代表了数据分布的"稳定程度"(书上写的所谓纯度)，或者说是"分布的离散程度"。用掰开揉碎的方式解释如下：如以下数据：技术能力积极度年龄前途 6 8 old normal 8 9 old yes 3 3 old no 7 5 old normal 7 7 young normal 7 6 old normal 8 5 old no

决策树算法ID3，C4.5， CART

决策树是机器学习中非常经典的一类学习算法，它通过树的结构，利用树的分支来表示对样本特征的判断规则，从树的叶子节点所包含的训练样本中得到预测值。决策树如何生成决定了所能处理的数据类型和预测性能。主要的决策树算法包括ID3，C4.5， CART等。 1，ID3 ID3是由 Ross Quinlan在1986年提出的一种构造决策树的方法。用于处理标称型数据集，其构造过程如下：输入训练数据是一组带

scikit-learn/ID3算法使用GridSearchCV调优

环境：python 3，scikit-learn 0.18 #coding:utf-8"""python 3scikit-learn 0.18"""from sklearn.model_selection import GridSearchCVfrom sklearn.model_selection import train_test_splitfrom sklearn.tree

scikit-learn/ID3手写数字识别

环境：python 3，scikit-learn 0.18 判定树是一个类似于流程图的树结构：其中，每个内部结点表示在一属性上的测试，每个分支代表一个属性输出，而每个树叶结点代表类或类分布。树的顶层是根结点。 ID3算法根据的就是信息获取量(Information Gain)：Gain(A) = Info(D) - Infor_A(D) #coding:utf-8"""python

ID3算法信息熵计算公式

gain.py import mathdef I(s1, s2):''':param s1: 值为1的数量:param s2: 值为0的数量:return: 返回期望值'''s = s1 + s2if s1 == 0 or s2 == 0:return 0# print("s1 = {}, s2 = {}, s = {}".format(s1,s2,s))ex = - (s1 / s)

经典决策树算法（ID3、C4.5、CART）原理以及Python实现

1 决策树简介决策树(Decision Tree)，是每个分支都通过条件判断进行划分的树，是解决分类和回归问题的一种机器学习算法，其核心是一个贪心算法，它采用自顶向下的递归方法构建决策树。 1.1 决策树模型决策树模型是一种对实例进行分类的树，由节点（node，由圆框表示）和有向边（directed edge，由方框表示）组成，其中节点分为内部节点（internal node）和叶子

ID3算法决策树学习 Python实现

算法流程输入：约束决策树生长参数（最大深度，节点最小样本数，可选），训练集（特征值离散或连续，标签离散）。输出：决策树。过程：每次选择信息增益最大的属性决策分类，直到当前节点样本均为同一类，或者信息增益过小。信息增益设样本需分为 K K K 类，当前节点待分类样本中每类样本的个数分别为 n 1 , n 2 , … , n K n_1, n_2, …, n_K n1,n2,…

2024美赛数学建模思路 - 案例：ID3-决策树分类算法

文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码建模资料 0 赛题思路（赛题出来以后第一时间在CSDN分享） https://blog.csdn.net/dc_sinor?type=blog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法，就是频繁模式树算法，他与Apriori算法一样也是用来挖掘频繁项集的

Python数据挖掘学习笔记（5）决策树分类算法----以ID3为例

一、相关原理决策树(Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。在机器学习中，决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系。E

分类——决策树ID3与C4.5以及Python实现

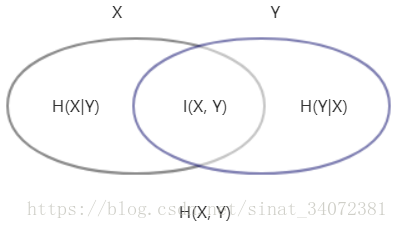
决策树算法是一个分类算法，ID3以及C4.5决策树是多叉树。核心思想：根据特征及对应特征值组成元组为切分点切分样本空间。基本概念：熵(entropy)：该词最初来自于热力学，用来表示系统的混乱程度。香农借用该词表示一个随机过程的不确定性程度，即香农熵。式中Pi指随机变量取某个值的概率。条件熵(conditional entropy)：给定一个划分数据的条件X=x，那么随机变量Y

决策树：ID3､C4.5､CART算法与Python实现

一、决策树的基本概念决策树(Decision Tree)算法是一类常用的机器学习算法，在分类问题中，决策树算法通过样本中某一些属性的值，将样本划分到不同的类别中。决策树跟人在做决策的思考方式很想像，先考虑重点选项，不符合则可最优先做出决策。

决策树DT：ID3、C4.5原理及python实现

文章目录决策树模型与学习特征选择信息增益信息增益比 ID3算法决策树生成ID3算法的不足 C4.5算法连续值处理缺失值处理C4.5算法的不足决策树剪枝程序实现ID3 决策树模型与学习决策树分类: 从根节点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到对应子节点；若子节点为特征的一个取值，则递归的对实例进行测试并分配，直到到达叶节点（类别）。决策树与条件概