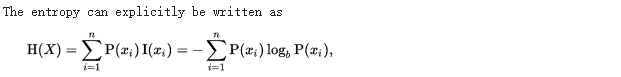本文主要是介绍基于ID3算法生成决策树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
决策树的类型有很多,有CART、ID3和C4.5等,其中CART是基于基尼不纯度(Gini)的,而ID3和C4.5都是基于信息熵的,它们两个得到的结果都是一样的,本次定义主要针对ID3算法。
在构造决策树时,第一个问题就是:当前的那个特征在划分数据是起着决定性的作用。为了找到决策性的特征必须对每个特征进行评估。因此本文针对ID3算法使用的信息熵方法划分数据的特征来进行实验。
信息熵
如果待分类的的事物有多种,比如有A,B,C三类,则A的信息为:
X(a)=-lon2(p(a)),即log以2为底的a出现的概率。
而熵的定义为信息的期望值,即:
在划分数据前和划分数据后信息方式的变化称为信息增益。因此我们找出信息增益最大的一个特征用来划分数据集。ID3的原理即使Gain达到最大值。信息增益即为熵的减少或者是数据无序度的减少.
计算信息熵
计算的公式见上图,在计算是要统计每个类别出现的次数,然后用公式去计算即可。
如求下列数据的信息熵,dataset为数据集,最后一列为类别,前两列为特征。
dataSet=[[1,1,'yes'],[1,1,'yes'],[1,0,'no'],[0,1,'no'],[0,1,'no']]def calShannon(dataSet): #这里的dataset为python列表形式m=len(dataSet) #得到样本个数labelCount={}for featVec in dataSet: #遍历每一个样本label=featVec[-1] #这里最后一列为样本的类别if label not in labelCount.keys():labelCount[label]=0labelCount[label]+=1shan=0.0for key in labelCount:prob=float(labelCount[key])/mshan -=prob * math.log(prob,2)print ("the shannon is %f " % shan) return shan将上述代码保存到tree.py中,然后运行,即可计算此数据的信息熵
>>> import tree
>>> dataSet=[[1,1,'yes'],[1,1,'yes'],[1,0,'no'],[0,1,'no'],[0,1,'no']]
>>> tree.calShannon(dataSet)
the shannon is 0.970951
0.9709505944546686划分数据集
按给定的特征划分数据集:
#特别注意这里的nFeat,所选择的数据特征,value为这个特征里的值
def split(dataSet,nFeat,value): #the num of feature ,and using value to split,datasetretData=[]for featVec in dataSet: #遍历样本if featVec[nFeat]==value: reducedVec=featVec[:nFeat]reducedVec.extend(featVec[nFeat+1:]) #this mean reduce the featureretData.append(reducedVec)return retData运行结果如下:
#第0个特征,值为1,返回的是去掉第0个特征后剩余的样本
>>> tree.split(dataSet,0,1)
[[1, 'yes'], [1, 'yes'], [0, 'no']]
>>> tree.split(dataSet,1,1)
[[1, 'yes'], [1, 'yes'], [0, 'no'], [0, 'no']]这里需要重点理解一下:
我如果选择第0个特征进行划分,那么在第0个特征中有许多不同的值,那么,应该计算这些不同值划分过后的信息熵之和,为以第0个特征划分后的信息熵。
举个例子,如果要以第0个特征划分数据,在第0个数据上有2个不同的值分别为0,1那么应该将数据划分为两部分,调用两次tree.split(dataSet,0,1),
tree.split(dataSet,0,0),然后分别求出他们的信息熵,再求和,就是最后所得的信息熵了。
因此理解上述的过程后,即可实现如何才是最好的样本划分方式:
这里解释一下: featList = [example[i] for example in dataSet]
python中的列表推到式,其中dataSet为样本,example每次取出一个样本,然后将这个样本的exampe[i]即第i个元素加到featlist中。
即此句的作用是快速的取出样本中第i个特征的所有值。
def chooseBestFeature(dataSet):numFeatures = len(dataSet[0]) - 1 #the last column is used for the labelsbaseEntropy = calShannon(dataSet) # the origin shannonbestInfoGain = 0.0; bestFeature = -1for i in range(numFeatures): #iterate over all the featuresfeatList = [example[i] for example in dataSet]#create a list of all the examples of this featureuniqueVals=set(featList) # have how many value in this featurenewShannon=0.0for value in uniqueVals:subDataSet=split(dataSet,i,value)prob=len(subDataSet)/float(len(dataSet))newShannon +=prob*calShannon(subDataSet)infoGain=baseEntropy-newShannonif infoGain>bestInfoGain:bestInfoGain=newShannonbestFeature=ireturn bestFeature 同样将上述代码加到tree.py中,运行得到:
>>> tree.chooseBestFeature(dataSet)
the shannon is 0.970951
the shannon is 0.000000
the shannon is 0.918296
the shannon is 0.000000
the shannon is 1.000000
0 #即最好的特质是0,它使得信息增益最大构建决策树
这里有几点需要说明:
1. 如果用完所有的特征仍然不能区分样本,则以投票算法返回
2. 如果为用完特征样本已经同属于一类,则直接返回
3. 递归处理
投票算法:
def majorityCnt(classList):classCount={}for vote in classList:if vote not in classCount.keys(): classCount[vote] = 0classCount[vote] += 1sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)return sortedClassCount[0][0]这里sorted我更喜欢写成:
sorted(classCount.items(), key=lambda x:x[1], reverse=True)
构造决策树:
def createTree(dataSet,labels):classList = [example[-1] for example in dataSet]if classList.count(classList[0]) == len(classList): return classList[0]#stop splitting when all of the classes are equalif len(dataSet[0]) == 1: #stop splitting when there are no more features in dataSetreturn majorityCnt(classList)bestFeat = chooseBestFeature(dataSet)bestFeatLabel = labels[bestFeat]myTree = {bestFeatLabel:{}}del(labels[bestFeat])featValues = [example[bestFeat] for example in dataSet]uniqueVals = set(featValues)for value in uniqueVals:subLabels = labels[:] #copy all of labels, so trees don't mess up existing labelsmyTree[bestFeatLabel][value] = createTree(split(dataSet, bestFeat, value),subLabels)return myTree 运行结果:
>>> data,label=tree.createDataSet()
>>> data
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
>>> label
['no surfacing', 'flippers']
>>> myTree=tree.createTree(data,label)
the shannon is 0.970951
the shannon is 0.000000
the shannon is 0.918296
the shannon is 0.000000
the shannon is 1.000000
the shannon is 0.918296
the shannon is 0.000000
the shannon is 0.000000
>>> myTree
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}myTree是用嵌套的字典来模拟树形结构。
这篇关于基于ID3算法生成决策树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!