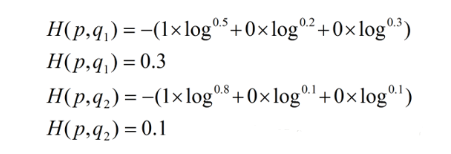entropy专题
![[深度学习]交叉熵(Cross Entropy)算法实现及应用](https://img-blog.csdn.net/20171016095220792?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdTAxMzI1MDQxNg==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)
[深度学习]交叉熵(Cross Entropy)算法实现及应用
写在前面：要学习深度学习，就不可避免要学习Tensorflow框架。初了解Tensorflow的基础知识，看到众多API，觉得无从下手。但是到了阅读完整项目代码的阶段，通过一个完整的项目逻辑，就会让我们看到的不只是API，而是API背后，与理论研究相对应的道理。除了Tensorflow中文社区的教程，最近一周主要在阅读DCGAN的代码（Github:https://github.com/carpe
数学基础 -- 均方误差（Mean Squared Error, MSE）与交叉熵（Cross-Entropy）的数学原理
均方误差（Mean Squared Error, MSE）与交叉熵（Cross-Entropy）的数学原理 1. 均方误差（Mean Squared Error, MSE） 均方误差主要用于回归问题，度量预测值与实际值之间的平均平方差。其数学公式为： MSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{n} \sum_{i
Cross_entropy和softmax
1. 传统的损失函数存在的问题 传统二次损失函数为： J ( W , b ) = 1 2 ( h W , b ( x ) − y ) 2 + λ 2 K ∑ k ∈ K w i j 2 J(W,b)=\frac 12(h_{W,b}(x)-y)^2+\frac \lambda{2K}\sum_{k \in K}w_{ij}^2 J(W,b)=21(hW,b(x)−y)2+2Kλk∈K∑
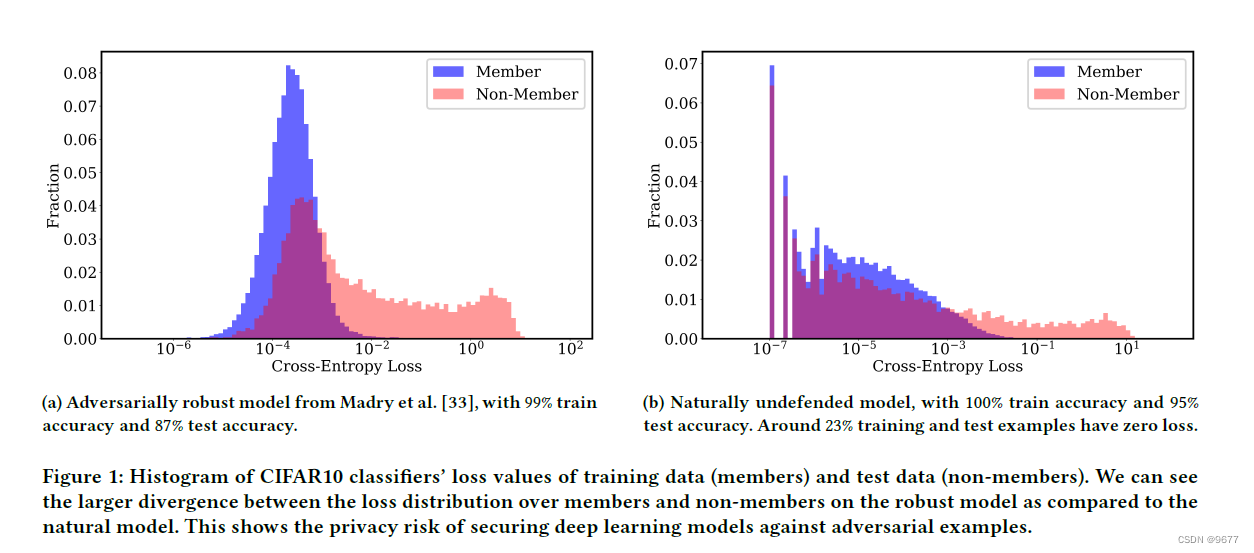
the histogram of cross-entropy loss values 交叉熵损失值的直方图以及cross-entropy loss交叉熵损失
交叉熵损失值的直方图在机器学习和深度学习中有几个重要的作用和用途： 评估模型性能: 直方图可以帮助评估模型在训练数据和测试数据上的性能。通过观察损失值的分布，可以了解模型在不同数据集上的表现情况。例如，损失值分布的形状和范围可以反映模型对训练数据的拟合程度以及在测试数据上的泛化能力。 检测过拟合和欠拟合: 直方图可以显示训练数据和测试数据的损失值分布是否存在偏差。过拟合情况下，模型在训练数据
FCN 喂入自己数据出错【Node：entropy/entropy = SparseSoftmaxCrossEntropyWithLogits...........】
[[Node:entropy/entropy=SparseSoftmaxCrossEntropyWithLogits[T=DT_FLOAT,Tlabels=DT_INT32,_device="/job:localhost/replica:0/task:0/device:CPU:0"](ent ropy/Reshape, entropy/Reshape_1)]] 这是个什么鬼？？？ 【解决办
uvalive 2088 - Entropy(huffman编码）
题目连接：2088 - Entropy 题目大意：给出一个字符串， 包括A~Z和_， 现在要根据字符出现的频率为他们进行编码，要求编码后字节最小， 然后输出字符均为8字节表示时的总字节数， 以及最小的编码方式所需的总字节数，并输出两者的比率， 保留一位小数。 解题思路：huffman编码。 #include <stdio.h>#include <string.h>#
F.cross_entropy 交叉熵损失
https://blog.csdn.net/wuliBob/article/details/104119616 Examples:: >>>import torch.nn.functional as F >>> input = torch.randn(3, 5, requires_grad=True) >>> target = torch
tf.nn.conv2,cross_entropy,loss,sklearn.preprocessing,next_batch,truncated_normal,seed,shuffle,argmax
tf.truncated_normal https://www.tensorflow.org/api_docs/python/tf/random/truncated_normal truncated_normal( shape, mean=0.0, stddev=1.0, dtype=tf.float32, seed=None, name=None ) seed: 随机种子，若 seed 赋值
分类模型的 Loss 为什么使用 cross entropy 而不是 classification error 或 squared error
提纲： 分类模型 与 Loss 函数的定义， 为什么不能用 Classification Error， Cross Entropy 的效果对比， 为什么不用 Mean Squared Error， 定量理解 Cross Entropy， 总结， 参考资料。 交叉熵定义：http://blog.csdn.net/lanchunhui/article/details/50970625
关于tensorflow中的softmax_cross_entropy_with_logits_v2函数的区别
tf.nn.softmax_cross_entropy_with_logits(记为f1) 和 tf.nn.sparse_softmax_cross_entropy_with_logits(记为f3),以及 tf.nn.softmax_cross_entropy_with_logits_v2(记为f2) 之间的区别。 f1和f3对于参数logits的要求都是一样的，即未经处理的，直接由神经
杭电OJ 1053：Entropy
这个问题的主要难点是构建huffman树，在构建huffman树的过程中可以使用优先队列，另外在计算总的编码长度的时候用了树的遍历算法。需要注意的是如果出现的字符只有一种，这种情况要单独考虑。下面的代码还给出了指针优先队列的用法（指针优先队列和值优先队列的用法不太一样）。 C++代码： #include<stdio.h>#include<queue>#include<string.h>
PyTorch使用F.cross_entropy报错Assertion `t ＞= 0 t ＜ n_classes` failed问题记录
前言 在PyTorch框架下使用F.cross_entropy()函数时，偶尔会报错ClassNLLCriterion ··· Assertion `t >= 0 && t < n_classes ` failed。 错误信息类似下面打印信息： /py/conda-bld/pytorch_1490981920203/work/torch/lib/THCUNN/ClassNLLCriter
损失函数：Cross Entropy Loss （交叉熵损失函数）
损失函数：Cross Entropy Loss （交叉熵损失函数） 前言相关介绍Softmax函数代码实例 Cross Entropy Loss （交叉熵损失函数）Cross Entropy Loss与BCE loss区别代码实例 前言 由于本人水平有限，难免出现错漏，敬请批评改正。更多精彩内容，可点击进入人工智能知识点专栏、Python日常小操作专栏、OpenCV-Pyth
tensorflow的cross_entropy(loss)=nan问题
解决方案1: cross_entropy = -tf.reduce_sum(y_*tf.log(tf.clip_by_value(y_conv,1e-10,1.0))) 解决方案2:(推荐) cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv + 1e-10)) 原文参考:http://stackoverflow.com/quest
机器学习----交叉熵(Cross Entropy)如何做损失函数
目录 一.概念引入 1.损失函数 2.均值平方差损失函数 3.交叉熵损失函数 3.1信息量 3.2信息熵 3.3相对熵 二.交叉熵损失函数的原理及推导过程 表达式 二分类 联立 取对数 补充 三.交叉熵函数的代码实现 一.概念引入 1.损失函数 损失函数是指一种将一个事件（在一个样本空间中的一个元素）映射到一个表达与其事件相关的经济成本或机会成本的实数上
halcon entropy_image 熵图像的计算 （by shany shang）
entropy_image(Image : ImageEntropy : Width, Height : ) 功能：计算输入图像（Image）的（Width*Height ）大小的区域的熵输出图像（ImageEntropy） 图像的一维熵： 其中Pi表示灰度值为i的像素所占的比例，也可认为是概率。 图像的一维熵可以表示图像灰度的聚集特征，熵越大，灰度值分布越均匀。却不能
tf.nn.softman_cross_entropy_with_logits及几种交叉熵计算
https://www.jianshu.com/p/95d0dd92a88a 就看例子就完事了 tf.nn.softmax import tensorflow as tfimport numpy as npsess=tf.Session()#logits代表wx+b的输出，并没有进行softmax（因为softmax后是一个和为1的概率）logits = np.array(
[分布外检测]Entropy Maximization and Meta Classification for Out-of-Distribution Detection...实现记录
Aomaly Segmentation 项目记录 该文档记录异常检测在自动驾驶语义分割场景中的应用。 主要参考论文Entropy Maximization and Meta Classification for Out-of-Distribution Detection in Semantic Segmentation 摘要： Deep neural networks (DNNs) for
交叉熵损失函数（Cross-Entropy Loss）的基本概念与程序代码
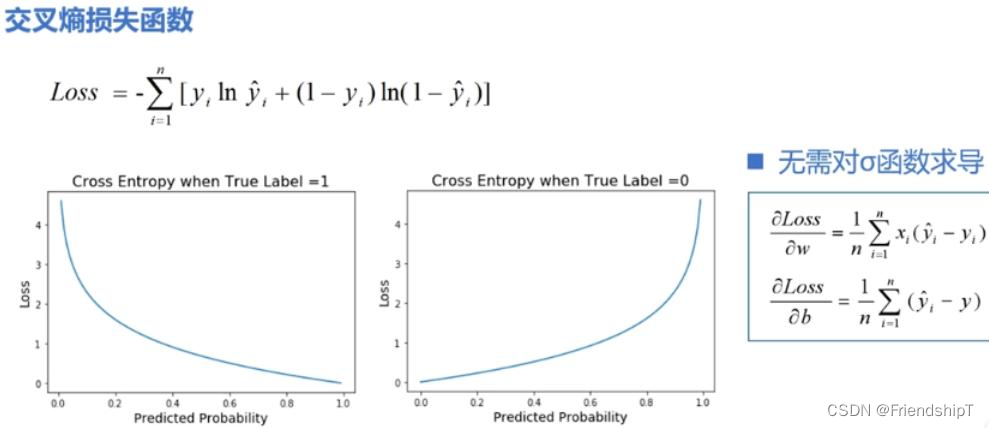
交叉熵损失函数（Cross-Entropy Loss）是机器学习和深度学习中常用的损失函数之一，用于分类问题。其基本概念如下： 1. 基本解释： 交叉熵损失函数衡量了模型预测的概率分布与真实概率分布之间的差异。在分类问题中，通常有一个真实的类别标签，而模型会输出一个概率分布，表示样本属于各个类别的概率。交叉熵损失函数通过比较这两个分布来计算损失，从而指导模型的优化。 具体来说，对于二分类
TensorFlow交叉熵函数(cross_entropy)·理解应用
Tensorflow的交叉熵理解应用可以参考： TensorFlow交叉熵函数(cross_entropy)·理解 - 简书 (jianshu.com)https://www.jianshu.com/p/cf235861311b 手写识别的交叉熵的理解，其中设计argmax()函数， TensorFlow入门(一) - mnist手写数字识别(网络搭建) | 极客兔兔 (geek
损失函数softmax_cross_entropy、binary_cross_entropy、sigmoid_cross_entropy之间的区别与联系
cross_entropy-----交叉熵是深度学习中常用的一个概念，一般用来求目标与预测值之间的差距。 在介绍softmax_cross_entropy，binary_cross_entropy、sigmoid_cross_entropy之前，先来回顾一下信息量、熵、交叉熵等基本概念。 --------------------- 信息论 交叉熵是信息论中的一个概念，要想了解交叉熵的本质，
【论文简述】Rethinking Cross-Entropy Loss for Stereo Matching Networks（arxiv 2023）
一、论文简述 1. 第一作者：Peng Xu 2. 发表年份：2023 3. 发表期刊：arxiv 4. 关键词：立体匹配，交叉熵损失，过渡平滑和不对准问题，跨域泛化 5. 探索动机：立体匹配通常被认为是深度学习中的一个回归任务，通常采用平滑L1损失结合Soft-Argmax估计器来训练网络，达到亚像素级的视差精度。然而，平滑L1损失缺乏对代价体的直接约束，在训练过程中容易出现过拟合。S
TensorFlow ValueError Only call softmax_cross_entropy_with_logits with named arguments labels logits
TensorFlow报错： ValueError: Only call softmax_cross_entropy_with_logits with named arguments (labels=…, logits=…, …) 定位到出错点： self.loss = tf.nn.softmax_cross_entropy_with_logits(z, self.target) 原来
多元排列熵 Multivariate Permutation Entropy
熵(Entropy) 信息论中熵的概念首次被香农提出，目的是寻找一种高效/无损地编码信息的方法：以编码后数据的平均长度来衡量高效性，平均长度越小越高效；同时还需满足“无损”的条件，即编码后不能有原始信息的丢失。这样，香农提出了熵的定义：无损编码事件信息的最小平均编码长度。 香农信息熵 Shannon entropy 香农信息熵是由香农提出的一个概念，它描述了信息源各可能事件发生的不确定性。这