halcon entropy_image 熵图像的计算 （by shany shang）

本文主要是介绍halcon entropy_image 熵图像的计算 （by shany shang），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

entropy_image(Image : ImageEntropy : Width, Height : )

功能：计算输入图像（Image）的（Width*Height ）大小的区域的熵输出图像（ImageEntropy）

图像的一维熵：

    其中Pi表示灰度值为i的像素所占的比例，也可认为是概率。

    图像的一维熵可以表示图像灰度的聚集特征，熵越大，灰度值分布越均匀。却不能表示图像灰度分布的空间特征。

    熵指的是体系的混乱的程度，对焦良好的图像的熵大于没有清晰对焦的图像，因此可以用熵作为一种对焦评价标准。熵越大，

图像越清晰。

此算子即是计算区域内的一维熵，后再将熵值乘以32赋值给区域中心像素。

延申：图像的二维熵：

选择图像的邻域灰度均值作为灰度分布的空间特征量，与图像的像素灰度组成特征二元组，记为(i,j)，其中i表示像素的灰度值(0<=i<=255)，j表示领域灰度均值(0<=j<=255)，即，可反应某像素位置上的灰度值与其周围像素的灰度分布的综合特征，其中f(i,j)为特征二元组(i,j)出现的频数，N为图像的尺度。

 

延申：计算交叉熵用于图像分割：

 第一步：在（Width*Height ）大小的区域进行背景分割，计算前景和背景的灰度均值

 第二步：设置阈值（从0到255遍历），找出使二值化分割前后图像的交叉熵最小的分割阈值

           

               交叉熵刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近。假设               概率分布p为期望输出，概率分布q为实际输出，H(p,q)为交叉熵，则：

 

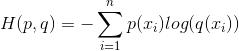
             这个公式如何表征距离呢，举个例子： 
             假设N=3，期望输出为p=(1,0,0)，实际输出q1=(0.5,0.2,0.3)，q2=(0.8,0.1,0.1)，那么：

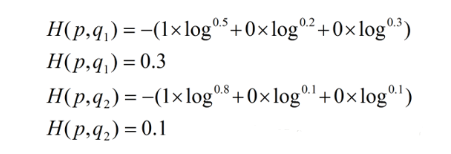
              很显然，q2与p更为接近，它的交叉熵也更小

 第三步：将大于分割阈值的灰度值设置为255，小于分割阈值的灰度值设置为0

这篇关于halcon entropy_image 熵图像的计算 （by shany shang）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---