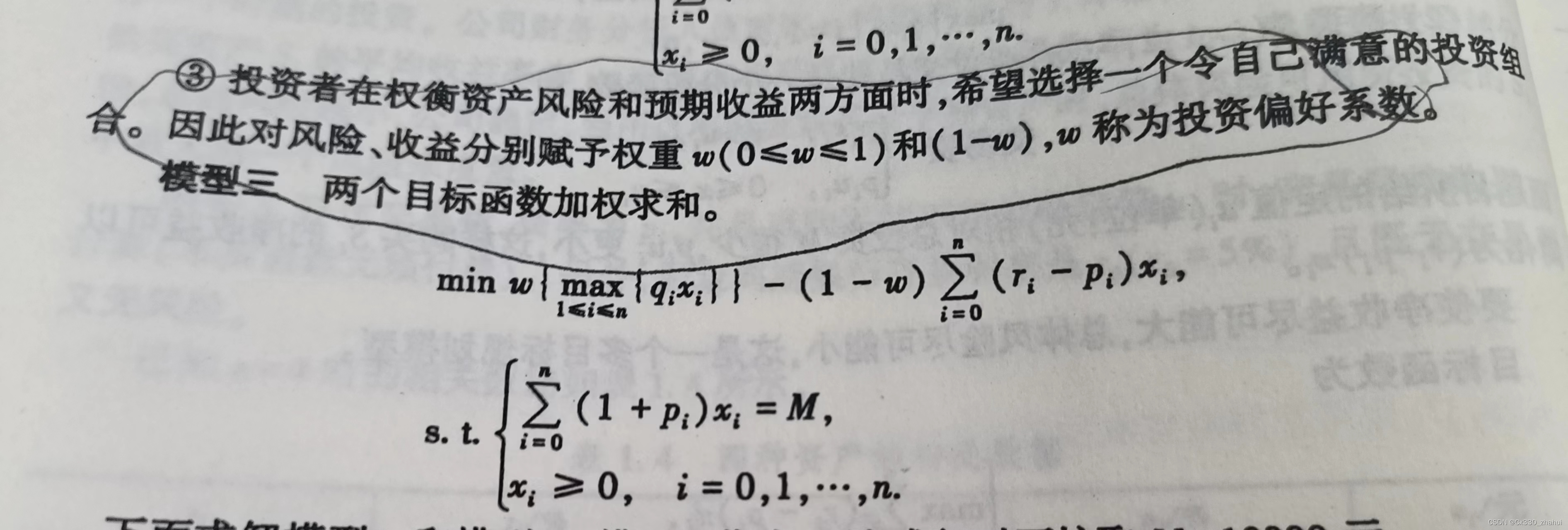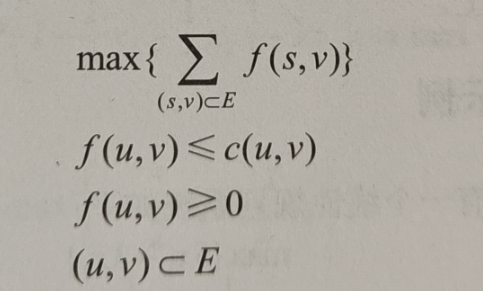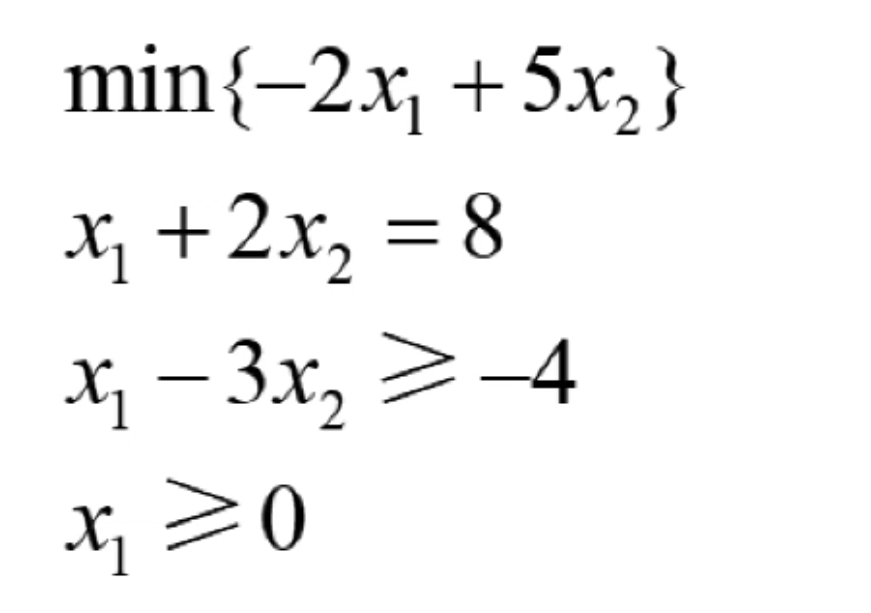线性规划专题
单纯形法 -- 求解线性规划
目前,运用最广的线性规划方法就是著名的单纯形方法。这种方法是G.B.Dantzig在1947年提出的。几十年的实践证明,单纯形方法的确是一种使用方便、行之有效的重要算法。如今,它已经成为线性规划的中心内容。 单纯形法的基本思路是有选择地取(而不是枚举所有的)基本可行解,即是从可行域的一个顶点出发,沿着可行域的边界移到另一个相邻的顶点,要求新顶点的目标函数值不比原目标函数值差,如此迭代,直至找到最
数学建模理论学习:线性规划模型
三要素:目标函数、约束条件(s.t.)、决策变量(x) 目标函数:z = ax1 + bx2 + cx3 + ... 其中c为一个序列,从左到右依次从x1到xn的系数 解决下面的线性规划问题: % 目标函数系数:-x1 - 2x2f = [-1; -2]; % 不等式约束 Ax <= b% A向量表示决策变量的系数,B向量表示的是对应的条件,若不符合Ax <= b需进行
【Lingo】线性规划入门
Lingo运算符 1.算术运算 ^ 乘方 ﹡ 乘 / 除 ﹢ 加 ﹣ 减 2.逻辑运算符 #not# 否定该操作数的逻辑值,#not#是一个一元运算符 #eq# 若两个运算数相等,则为true;否则为flase #ne# 若两个运算符不相等,则为true;否则为flase #gt# 若左边的运算符严格大于右边的运算符,则为true;否则为flase
线性规划问题——单纯形算法
第一步:化“约束标准型” 在每个等式约束中至少有一个变量的系数为正,且这个变量只在该约束中出现。在每个约束方程中选择一个这样的变量称为基本变量。 剩下变量称为非基本变量。 一个简单的栗子 上图是一个约束标准型线性规划的例子。 等式1:x₁+3x₂-x₃+2x₅=7 x₁,x₂,x₅ 的系数为正,但是等式2和3中有 x₂,等式3中有 x₅;所以等式1的基本变量是 x₁。 等
uva 11971 - Polygon(线性规划)
题目连接:uva 11971 - Polygon 题目大意:给定一个长度为N的线段,要求切K刀,分成K+1个线段,问能组成K+1边形的概率。 解题思路:K条线段能组成K边形的条件为任意一条边小于其他所有边的和,因为是求概率,所以和N无关。 根据高中线性规划的知识,以二维为例: 所以有ans=2K−K−12K #include <cstdio>#include <cstri
运筹学_3.运输问题(特殊的线性规划)
目录 前言3.1 平衡运输问题中初始基可行解确定运输问题平衡运输与非平衡运输平衡运输问题的数学模型单纯形法解决平衡运输问题,初始可行基的确认 3.2 平衡运输问题的最优解判别求检验数表上作业法 3.3 产销不平衡的运输问题运输问题中产大于销的问题运输问题中产小于销的问题 前言 运输问题是一类具有特殊结构的线性规划问题,运输问题由于约束方程组的特殊性,存在着比单纯形法更简单的特殊
Mathematica 随机生成一堆线性规划的式子
嘛,讲道理直接LinearProgramming就完事了 看第一种用法 LinearProgramming[c,m,b]求向量 x,使 c.x 在约束条件 m.x>=b 和 x>=0 下达到极小. 很明显c是向量,m是系数矩阵,b是列矩阵,随机生成这些东西丢进去就是了 不过内容似乎与标题不符,那就~ With[{n=10},Evaluate[Plus@@Table[Slot@i
MatLab建模学习笔记7——线性规划问题求解
线性规划(Linear programming,简称LP)是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法。研究线性约束条件下线性目标函数的极值问题的数学理论和方法。 线性规划步骤一般如下: (1)列出约束条件及目标函数 (2)画出约束条件所表示的可行域 (3)在可行域内求目标函数的最优解及最优值 线性规划中单纯形法的基本思路:先找
线性规划问题和MATLAB函数linprog的使用
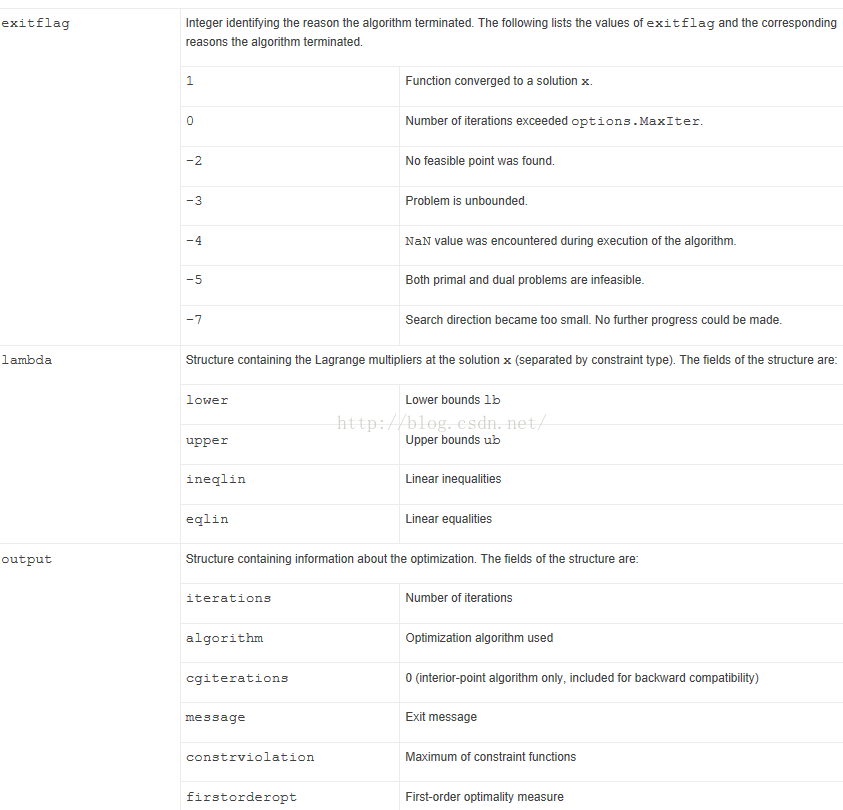
转自:http://blog.csdn.net/jbb0523/article/details/50596555 题目:线性规划问题和MATLAB函数linprog的使用 线性规划(Linear Programming, LP)问题的一般形式为: 其中。矩阵向量形式为 其中, , 线线规划的几个基本性质:【文献[1]第
线性规划-pulp-复杂矩阵
线性规划-pulp-复杂矩阵 1. 简介-线性规划 在数学中,线性规划(Linear Programming,简称LP)特指目标函数和约束条件皆为线性的最优化问题。线性规划是最优化问题中的一个重要领域。在作业研究中所面临的许多实际问题都可以用线性规划来处理,特别是某些特殊情况。最简单情况就,解线性方程组。 举个最简单的例子: 工厂生产A和B两种物品,需要原料配比分别是1:2:1和2:1:3
【数学建模】天然肠衣搭配问题衍生问题/线性规划限制条件建立问题
线性规划限制条件建立问题 前景回顾/提出问题回顾1回顾2/问题提出解决前提 解决方法坐标轴(区间)法总结 前景回顾/提出问题 回顾1 首先回顾一下DVD在线租赁问题 在 question2中,需要保证每个人都不会收到自己不喜欢的DVD,即客户在线订单数为0时候,不可以租给他。我直接给出答案了: x i j ≤ o r d e r i j , i = 1 , 2 , 3 ,
01数学建模 -线性规划
1.1线性规划–介绍 翻译翻译什么叫惊喜 1.2线性规划–原理 拉格朗日乘数法手算 最值化 f ( x , y ) , s . t . g ( x , y ) = c , 引入参数 λ ,有: F ( x , y , λ ) = f ( x , y ) + λ ( g ( x , y ) − c ) 再将其分别对 x , y , λ 求导,求当其结果为 0 时,对应的值,即可求得驻
数学建模--深入剖析线性规划(模型全方位解读+代码分析)
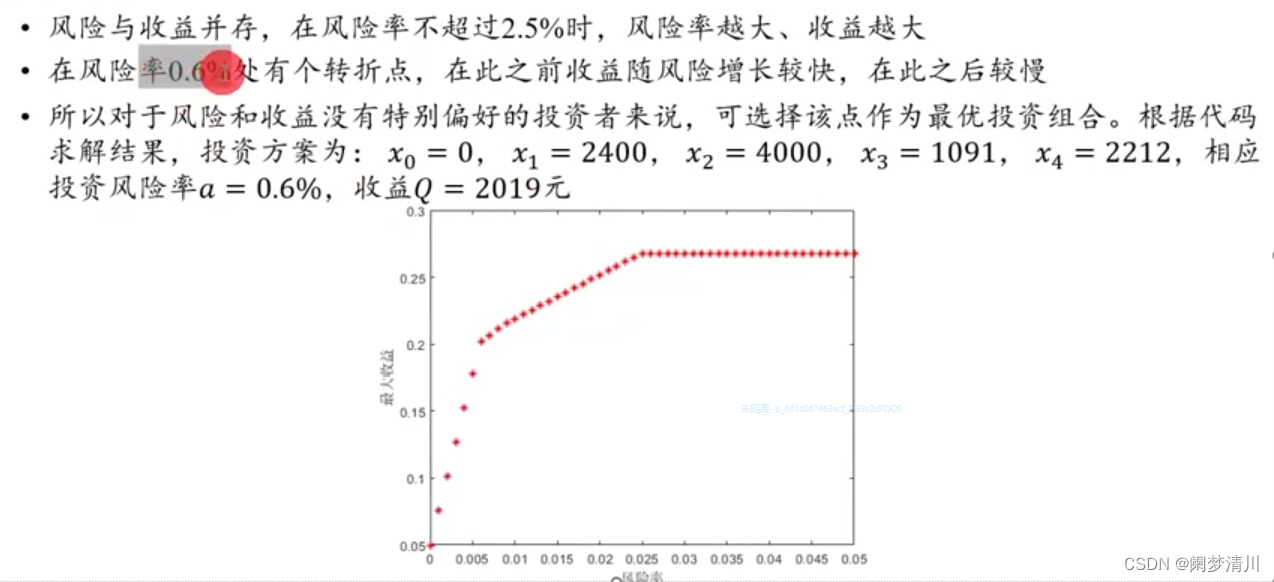
1.简介 (1)线性规划三要素 (2)模型适用赛题 2.典例讲解 (1)问题分析 目标函数是净收益尽可能大,风险尽可能小; 约束条件是交易费的分段函数,以及每一笔投资都是非负数; (2)模型假设 模型假设是我们进行建模的时候必须要进行的,我们应该逐步地学习;对于这道题目,我们首先要理清各个变量的
数模 线性规划模型理论与实践
线性规划模型理论与实践 1.1 线性规划问题 在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济效益的问题。此类问题构成了运筹学的一个重要分支一数学规划,而线性规划(Linear Programming 简记LP)则是数学规划的一个重要分支。自从1947年 G . B . D a n t z i g G.B.Dantzig G.B.Dantzig提出求解线性规划的单纯形方
Uoj #179 线性规划 单纯形算法
这是一道模板题。 (这个题现在标程挂了。。哪位哥哥愿意提供一下靠谱的标程呀?) 本题中你需要求解一个标准型线性规划: 有 n n 个实数变量 x 1 , x 2 ,…, x n x1,x2,…,xn 和 m m 条约束,其中第 i i 条约束形如 ∑ n j=1 a ij x j ≤ b i ∑j=1naijxj≤bi 。 此外
【线性规划与网络流24题#24】骑士共存
问题描述 在一个n×n个方格的国际象棋棋盘上,马(骑士)可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍,骑士不得进入。 对于给定的n*n个方格的国际象棋棋盘和障碍标志,计算棋盘上最多可以放置多少个骑士,使得它们彼此互不攻击。 输入格式 第一行有2 个正整数n 和m (1<=n<=200, 0<=m<n2), 分别表示棋盘的大小和障碍数。接下来的m 行给出障碍的位置。每行2 个正整数,表示
数学建模(1):线性规划
首先明确,线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最小的问题。 在解决这类型的实际问题时,应当选择适当的决策变量来建立有效模型。在数学建模中,涉及到线性规划的问题有以下几个类型: §1 一般线性规划 简单的线性规划问题都可使用matlab或lingo来处理。但对于matlab来说,所给定的模型必须满足标准型。因此,在matlab中,往往需要人工转化再输入计算。 标准
【数学建模】线性规划
针对未来可能的数学建模比赛内容,我对学习的内容做了一些调整,所以先跳过灰色关联分析和模糊综合评价的代码,今天先来了解一下运筹规划类——线性规划模型。 背景: 某数学建模游戏有三种题型,分别是A,B,C题。 每天有100体力,通过反复练习A,B,C题使自己的经验升级;通关A题可以获得20点经验,通关B题可以获得30点经验,通过C题可以获得45点经验做题会消耗体力,通关A消耗
用matlab求解线性规划
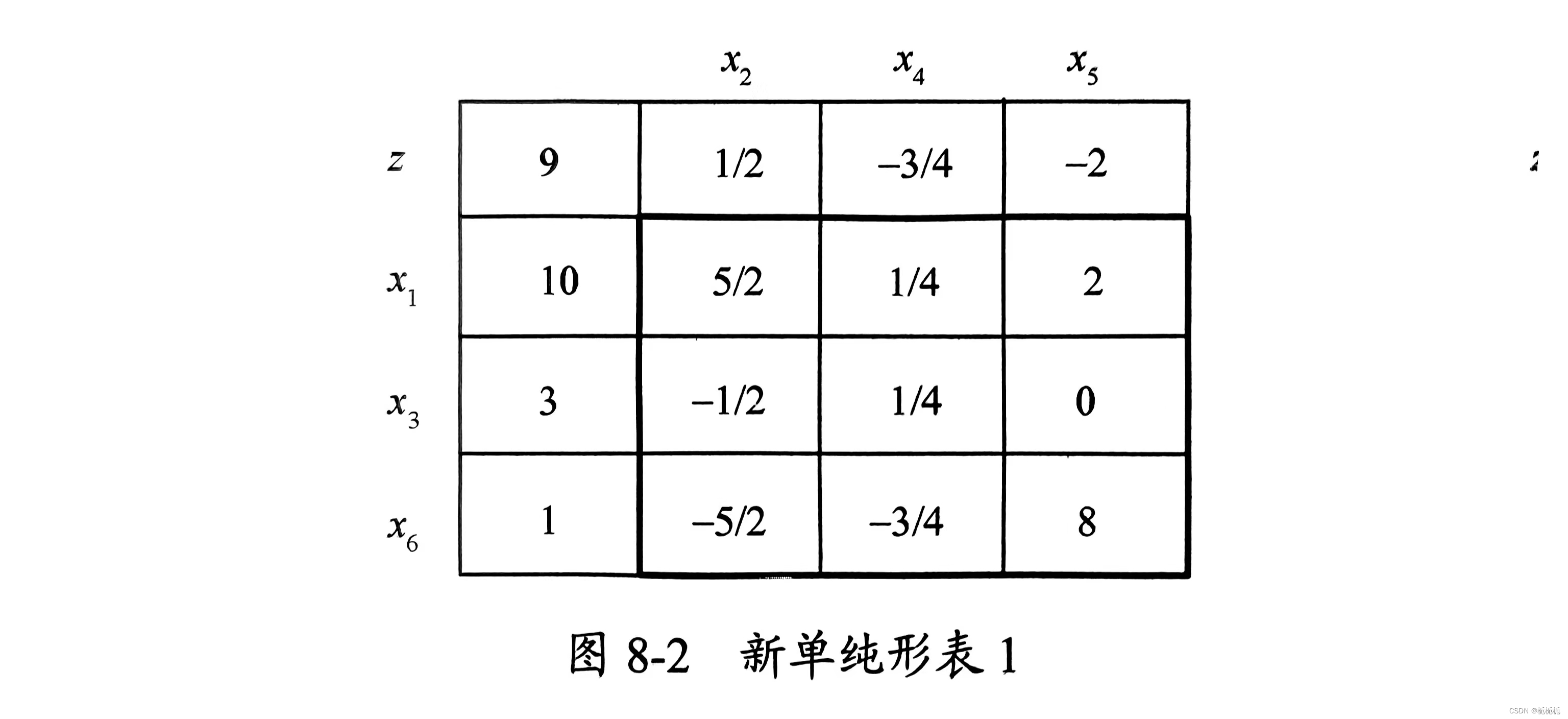
文章目录 1、用单纯形表求解线性规划绘制单纯形表求解: 2、用matlab求解线性规划——linprog()函数问题:补充代码:显示出完整的影子价格向量 1、用单纯形表求解线性规划 求解线性规划 m i n − 3 x 1 − 4 x 2 + x 3 min -3x_1-4x_2+x_3 min−3x1−4x2+x3, 约束条件为 2 x 1 + 3 x 2 ≤ 1
运筹学_1.1.4 线性规划问题-解的概念
1.1.4 线性规划问题-解的概念 一、可行解与最优解二、基的概念三、基变量、基向量;非基变量、非基向量;基解、基可行解;四、最优解与可行解、基可行解的关系五、用例题(枚举法)巩固基解、基可行解、最优解三个概念1、例12、例2 六、解之间的关系归纳 一、可行解与最优解 可行解:满足所由约束条件的解【全部可行解的集合称为可行域】 最优解:使目标函数最大的可行解 因此最优解包含
运筹学_1.2线性规划问题的几何意义
1.2线性规划问题的几何意义 一、凸集的基本概念二、由线性规划问题的几何意义、定理得出的几点结论三、引出单纯形法的解题步骤 一、凸集的基本概念 通俗来说,一个图形上任意两个点的连线上的点全部存在于这个图形中 二、由线性规划问题的几何意义、定理得出的几点结论 三、引出单纯形法的解题步骤
线性规划在多种问题形式下的应用
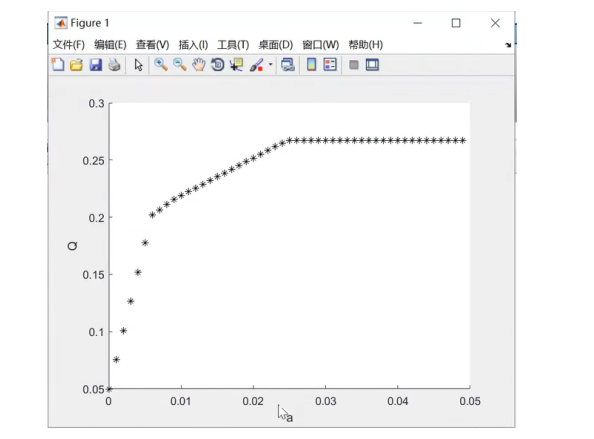
线性规划的用处非常的广泛,这主要是因为很多类型的问题是可以通过转化的方式转化为线性规划的问题。例如需要再图论中寻找起始点到给定的点的最短路径问题: 添加图片注释,不超过 140 字(可选) 假设要计算从节点0到节点4的最短路径,用变量d1到d4来表示节点0到节点1,2,3,4的最短路径,那么解决这个问题的本质上是解决如下的一个线性规划系统: 添加图片注释,不超过 140 字(
线性规划的标准型转换
对于任意给定的线性规划的问题,其实其本身可能是不符合线性规划标准型的需求的,但是如果通过一系列的等价变化的话,是可以将该问题转换为标准型的线性规划问题,例如如下的线性规划问题: 添加图片注释,不超过 140 字(可选) 给定的线性规划问题存在若干方面不满足最小值,首先就是目标函数是求最小值而不是求最大值,其次就是约束条件中的第2个不等式是大于等于而不是小于等于,最后就是这个问题只要求x
机械臂速成小指南(十六):带抛物线过渡的线性规划
👨🏫🥰🥳需要机械臂相关资源的同学可以在我的CSDN主页中找到哦🤖😽🦄 指南目录📖: 🎉🎉机械臂速成小指南(零点五):机械臂相关资源🎉🎉 机械臂速成小指南(零):指南主要内容及分析方法 机械臂速成小指南(一):机械臂发展概况 机械臂速成小指南(二):机械臂的应用 机械臂速成小指南(三):机械臂的机械结构 机械臂速成小指南(四):机械臂关键部件之减速机