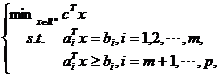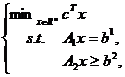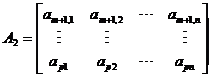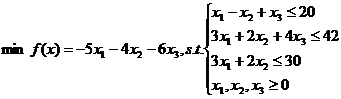本文主要是介绍线性规划问题和MATLAB函数linprog的使用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
转自:http://blog.csdn.net/jbb0523/article/details/50596555
题目:线性规划问题和MATLAB函数linprog的使用
线性规划(Linear Programming, LP)问题的一般形式为:
其中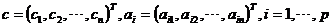
其中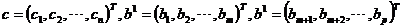
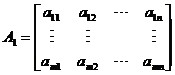
线线规划的几个基本性质:【文献[1]第46页】
(1)线性规划问题的可行域如果非空,则是一个凸集-凸多面体;
(2)如果线性规划问题有最优解,那么最优解可在可行域的顶点中确定;
(3)如果可行域有界,且可行域只有有限个顶点,则问题的最优解必存在,并在这有限个顶点中确定;
(4)最优解可由最优顶点处的有效约束形成的方程组的解确定。
常用的线性规划求解方法有单纯形法和内点法。
1、单纯形法(simplex method)
单纯形法是由G.B. Dantzig在1947年提出来的,这是20世纪数学界最重大的成果之一。单纯形法是一种迭代法,它根据线性规划问题的特点在问题可行域的顶点中逐步确定问题的最优解。在每一个是基本可行解的迭代点(即顶点),如果它不是最优的,单纯形法从与该顶点相连结的边中确定一个使目标函数值下降的边,沿该边移动可以确定一个与该顶点相邻且目标函数又优于该顶点的新顶点(新的基本可行解)。由于可行域的顶点数是有限的,如果每一次的移动都能使目标函数值下降,则经过有限次的移动方法必终止于问题的一个最优顶点。【文献[1]第57页】
单纯形法要求线性规划具有标准形式,即
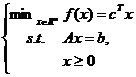
即约束函数都是等式约束,且决策变量均是非负的。
任何线性规划问题使用单纯形法时都需要通过变换转换为线性规划的标准形。转换方法参见文献[1]第51页例2.1.6。
2、从单纯形法到内点法
由于单纯形法的有效性,几十年来得到了广泛的应用。近年来,对于大规模的线性规划问题,尽管单纯形法受到了内点法的挑战,但单纯形法还是受到广大用户的青睐。
一个算法如果其求得问题的解所用的运算工作量是问题的参数m和n的多项式,则称这一算法的复杂多项式时间算法;如果所需运算工作量的阶数是以m或n为幂的指数2m或2n,则称复杂性是指数时间的算法。
单纯形算法的平均运算工作量是多项式时间的,但对于一个具体的问题其算法的复杂性并不一定是多项式的。1972年,Klee和Minty给出了一个复杂性为指数时间的例子。那么对线性规划问题是否存在时间复杂性是多项式的算法呢?如果存在多项式时间算法,如何设计这样的算法?
1979年,前苏联数学家Khachiyan回答了第1个问题,他提出了一个椭球算法求不等式问题的解,并证明了算法的时间复杂性是多项式的。利用对偶理论,线性规划问题可以转换成不等式问题,这就明确回答了对线性规划存在多项式时间算法。但是计算的实际表明,椭球算法的效果要比单纯形方法差得多,并不是一个有实际应用价值的算法。
1984年,在美国贝尔实验室工作的印度数学家Karmarkar回答了第2个问题,它对线性规划的求解提出了一个具有多项式时间复杂性的内点算法。
3、内点法(interior point method)
求线性规划问题的单纯形方法在问题的基本可行解中确定最优解,在几何上,每次迭代它是沿着可行域的边界从一个顶点向另一个更好的顶点移动来实现的。内点算法则完全不同,它是从可行域的一个严格内点开始,产生一个使目标函数值逐步改善的严格内点序列,并最终收敛于问题的最优解。通过下图可以清晰的看出单纯形法与内点法的区别。
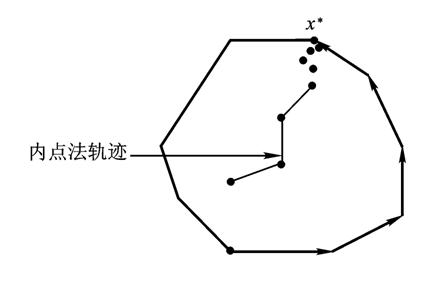
单纯形法与内战法轨迹(文献[1]图2.4.4)
经过近20年的研究与发展,如今已有大量求解线性规划问题的内点算法,它们可以分成三类:路径跟踪算法,仿射调比算法,和原始对偶内点算法(primal-dual interior point method)。
4、线性规划问题的MATLAB求解
在MATLAB中求解线性规划问题的函数是linprog,该函数集中了几种求线性规划的算法,如内点法和单纯形法,根据问题的规模或用户指定的算法进行求解。具体使用方法可查询帮助文件。

例:求如下线性规划问题。
输入以下代码:(代码是直接在Command Window中一行一行录入的,所以每行前面有符号“>>”)
输出以下结果:
参考文献:【1】孙文瑜, 徐成贤, 朱德通.最优化方法(第二版)[M]. 北京:高等教育出版社, 2010.
【2】龚纯,王正林. 精通MATLAB最优化计算[M].北京: 电子工业出版社,2009.
这篇关于线性规划问题和MATLAB函数linprog的使用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!