机械臂速成小指南（十六）：带抛物线过渡的线性规划

2024-02-19 14:40
文章标签 指南 十六 机械 线性规划 过渡 速成 抛物线

本文主要是介绍机械臂速成小指南（十六）：带抛物线过渡的线性规划，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

👨‍🏫🥰🥳需要机械臂相关资源的同学可以在我的CSDN主页中找到哦🤖😽🦄

指南目录📖：

🎉🎉机械臂速成小指南（零点五）：机械臂相关资源🎉🎉

机械臂速成小指南（零）：指南主要内容及分析方法

机械臂速成小指南（一）：机械臂发展概况

机械臂速成小指南（二）：机械臂的应用

机械臂速成小指南（三）：机械臂的机械结构

机械臂速成小指南（四）：机械臂关键部件之减速机

机械臂速成小指南（五）：末端执行器

机械臂速成小指南（六）：步进电机驱动器

机械臂速成小指南（七）：机械臂位姿的描述方法

机械臂速成小指南（八）：运动学建模（标准DH法）

机械臂速成小指南（九）：正运动学分析

机械臂速成小指南（十）：可达工作空间

机械臂速成小指南（十一）：坐标系的标准命名

机械臂速成小指南（十二）：逆运动学分析

机械臂速成小指南（十三）：轨迹规划概述

机械臂速成小指南（十四）：多项式插值轨迹规划

机械臂速成小指南（十五）：线性规划

机械臂速成小指南（十六）：带抛物线过渡的线性规划

机械臂速成小指南（十七）：直线规划 

机械臂速成小指南（十八）：圆弧规划

机械臂速成小指南（十九）：机械臂的电路板抓取实验

机械臂速成小指南（二十）：机械臂的位姿重复性实验

机械臂速成小指南（二十一）：几何雅可比矩阵

机械臂速成小指南（二十二）：机械臂逆运动学的数值解方法

机械臂速成小指南（二十三）：Paul方法求解机械臂运动学逆解（含matlab代码） 

🦾🌏🪐以下为正文🦾🌏🪐

        在上一章文末我们提到了线性规划的缺点：在起始点与终止点处存在速度的突变。因此，为了保证机械臂在起始与终止时的作业稳定性、安全性与精准性，我们使用抛物线对关节运动曲线进行过渡，这种关节空间轨迹规划方法称为带抛物线（parabolic）过渡的线性规划，使得关节角速度能以平滑的方式进行改变。

机械臂轨迹规划之带抛物线过渡的线性规划(关节空间)matlab仿真代码icon-default.png?t=N7T8https://download.csdn.net/download/m0_53966219/87521947?spm=1001.2014.3001.5503

一、理论分析

带抛物线拟合的线性规划

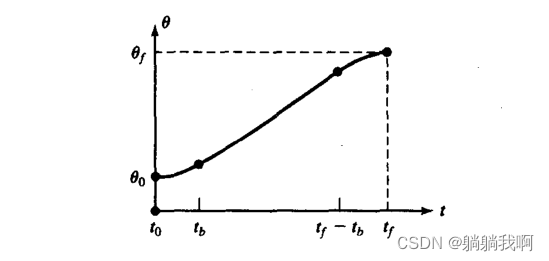
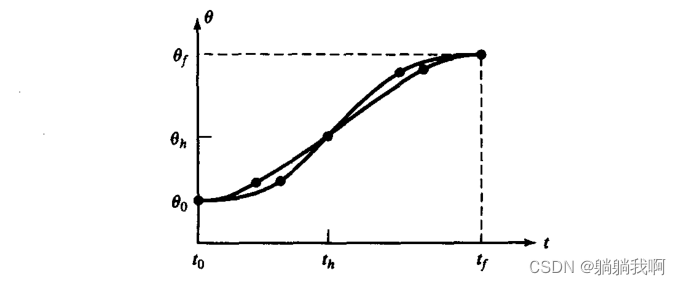
注：上图仅起到便于读者理解的作用，符号可能与下文不同

        为便于计算，我们设起始拟合段与终止拟合段的持续时间一致，二者关于轨迹中点(t_mid,θ_mid) 中心对称，且拥有大小相等、符号相反的恒定角加速度。

        设 为抛物线拟合区域的角加速度，t_acc 为拟合区域的持续时间，θ_a 为起始拟合段终点角度值。由于起始拟合段终点的速度必须等于直线段的速度，则有

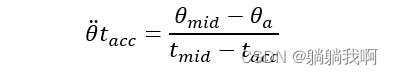
其中 而θ_a 可表示为

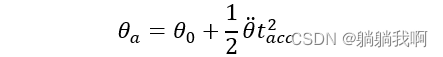
 联立上方两个式子，我们可以得到

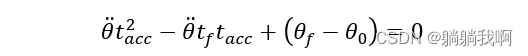
接着，求解t_acc ，得到

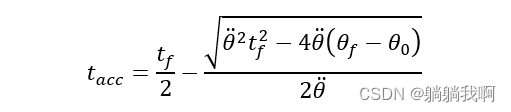
        我们注意到，上式可解的条件是抛物线拟合区域的加速度 满足

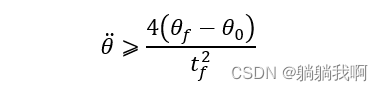
        当上式等号成立时，关节运动曲线将不存在直线段，而是仅由两段抛物线组成；而当 趋于无穷大时，所规划的关节运动曲线将重新变为一条直线，即回到线性规划的情况。

二、程序仿真

        使用MATLAB对由抛物线过渡的线性插值的轨迹规划方法进行仿真。

机械臂轨迹规划之带抛物线过渡的线性规划(关节空间)matlab仿真代码icon-default.png?t=N7T8https://download.csdn.net/download/m0_53966219/87521947?spm=1001.2014.3001.5503

第一步，定义机械臂的DH参数

%定义关节角度限制
lim1_min = -170 * radian1; lim1_max = 170 * radian1; %关节1(-170，170)
lim2_min = -132 * radian1; lim2_max =   0 * radian1; %关节2(-132，0)
lim3_min =    1 * radian1; lim3_max = 141 * radian1; %关节3(1，141)
lim4_min = -165 * radian1; lim4_max = 165 * radian1; %关节4(-165，165)
lim5_min = -105 * radian1; lim5_max = 105 * radian1; %关节5(-105，105)
lim6_min = -155 * radian1; lim6_max = 155 * radian1; %关节6(-155，155)
%定义关节旋转范围
lim1 = lim1_max - lim1_min;
lim2 = lim2_max - lim2_min;
lim3 = lim3_max - lim3_min;
lim4 = lim4_max - lim4_min;
lim5 = lim5_max - lim5_min;
lim6 = lim6_max - lim6_min;
%D-H参数表
theta1 = 0;    d1 = 169.77;     a1 = 64.2;    alpha1 = -pi/2;    offset1 = 0;
theta2 = 0;    d2 = 0;          a2 = 305;     alpha2 = 0;        offset2 = 0;
theta3 = 0;    d3 = 0;          a3 = 0;       alpha3 = pi/2;     offset3 = pi/2;
theta4 = 0;    d4 = -222.63;    a4 = 0;       alpha4 = -pi/2;    offset4 = 0;
theta5 = 0;    d5 = 0;          a5 = 0;       alpha5 = pi/2;     offset5 = 0;
theta6 = 0;    d6 = -36.25;     a6 = 0;       alpha6 = 0;        offset6 = -pi;

第二步，运动学建模

L(1) = Link([theta1, d1, a1, alpha1, offset1], 'standard');
L(2) = Link([theta2, d2, a2, alpha2, offset2], 'standard');
L(3) = Link([theta3, d3, a3, alpha3, offset3], 'standard');
L(4) = Link([theta4, d4, a4, alpha4, offset4], 'standard');
L(5) = Link([theta5, d5, a5, alpha5, offset5], 'standard');
L(6) = Link([theta6, d6, a6, alpha6, offset6], 'standard');
% 定义关节范围
L(1).qlim=[lim1_min,lim1_max];
L(2).qlim=[lim2_min,lim2_max];
L(3).qlim=[lim3_min,lim3_max];
L(4).qlim=[lim4_min,lim4_max];
L(5).qlim=[lim5_min,lim5_max];
L(6).qlim=[lim6_min,lim6_max];  
robot = SerialLink(L,'name','AR3');

第三步，定义起始点、终止点以及储存关节角度、角速度、角加速度的数组

T1=transl(-100,-100,300);				%齐次变换矩阵
T2=transl(200,-200,400);				%齐次变换矩阵
init_ang=robot.ikine(T1);				%运动学逆解
targ_ang=robot.ikine(T2);				%运动学逆解
q = zeros(step,N);   %初始化机械臂的位置
qd = zeros(step,N);  %初始化机械臂的角速度
qdd = zeros(step,N); %初始化机械臂的角加速度

第四步，计算抛物线公式

step = 50;                      %总步长，也可看作总时间
t_mid = step / 2;               %时间中点
t_acc = 10;                     %抛物线拟合段的持续步长(时间)
middle_ang = (targ_ang - init_ang) / 2 + init_ang;      %计算角度中值
a_ang = init_ang + (targ_ang - init_ang) / 12;           %定义起始抛物线拟合段的终点角度值
a_velocity = (middle_ang - a_ang) / (t_mid - t_acc);    %终止抛物线拟合段的终点角速度值
acceleration = a_velocity / t_acc;                      %加速度

第五步，进行轨迹规划

for t = 1:step% 起始抛物线拟合段if t <= t_accq(t,:)   = acceleration * (t)^2 / 2 + init_ang;  %位置qd(t,:)  = acceleration * t;                     %角速度qdd(t,:) = acceleration;                         %角加速度% 直线段elseif (t > t_acc) && (t <= step - t_acc)q(t,:)   = a_velocity * (t - t_acc) + q(t_acc,:);%位置qd(t,:)  = a_velocity;                           %角速度qdd(t,:) = 0;                                    %角加速度% 终止抛物线拟合段elseq(t,:)   = q(step - t_acc,:) + a_velocity * (t - (step - t_acc)) - acceleration * (t - (step - t_acc))^2 / 2;%位置qd(t,:)  = a_velocity - acceleration * (t + t_acc - step);                                                   %角速度qdd(t,:) = -acceleration;                                                                                    %角加速度end
end

效果如下图所示

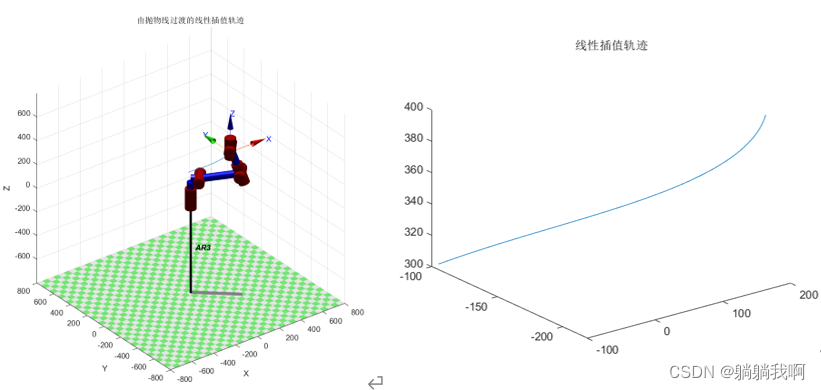
机械臂轨迹规划之带抛物线过渡的线性规划(关节空间)matlab仿真代码icon-default.png?t=N7T8https://download.csdn.net/download/m0_53966219/87521947?spm=1001.2014.3001.5503

三、编程实现

        机械臂在运行过程中较为平稳，且在作往复运动时，臂体振动幅度变小。

这篇关于机械臂速成小指南（十六）：带抛物线过渡的线性规划的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/724990。

相关文章

Retrieval-based-Voice-Conversion-WebUI模型构建指南

Retrieval-based-Voice-Conversion-WebUI模型构建指南

一、模型介绍 Retrieval-based-Voice-Conversion-WebUI（简称 RVC）模型是一个基于 VITS（Variational Inference with adversarial learning for end-to-end Text-to-Speech）的简单易用的语音转换框架。 具有以下特点 简单易用：RVC 模型通过简单易用的网页界面，使得用户无需深入了
阅读更多...
Java 创建图形用户界面（GUI）入门指南（Swing库 JFrame 类）概述

Java 创建图形用户界面（GUI）入门指南（Swing库 JFrame 类）概述

概述 基本概念 Java Swing 的架构 Java Swing 是一个为 Java 设计的 GUI 工具包，是 JAVA 基础类的一部分，基于 Java AWT 构建，提供了一系列轻量级、可定制的图形用户界面（GUI）组件。 与 AWT 相比，Swing 提供了许多比 AWT 更好的屏幕显示元素，更加灵活和可定制，具有更好的跨平台性能。 组件和容器 Java Swing 提供了许多
阅读更多...
基于UE5和ROS2的激光雷达+深度RGBD相机小车的仿真指南(五)：Blender锥桶建模

基于UE5和ROS2的激光雷达+深度RGBD相机小车的仿真指南(五)：Blender锥桶建模

前言 本系列教程旨在使用UE5配置一个具备激光雷达+深度摄像机的仿真小车，并使用通过跨平台的方式进行ROS2和UE5仿真的通讯，达到小车自主导航的目的。本教程默认有ROS2导航及其gazebo仿真相关方面基础，Nav2相关的学习教程可以参考本人的其他博客Nav2代价地图实现和原理–Nav2源码解读之CostMap2D(上)-CSDN博客往期教程： 第一期：基于UE5和ROS2的激光雷达+深度RG
阅读更多...
如何掌握面向对象编程的四大特性、Lambda 表达式及 I/O 流：全面指南

如何掌握面向对象编程的四大特性、Lambda 表达式及 I/O 流：全面指南

这里写目录标题 OOP语言的四大特性lambda输入/输出流（I/O流） OOP语言的四大特性 面向对象编程（OOP）是一种编程范式，它通过使用“对象”来组织代码。OOP 的四大特性是封装、继承、多态和抽象。这些特性帮助程序员更好地管理复杂的代码，使程序更易于理解和维护。 类-》实体的抽象类型 实体（属性，行为） -》 ADT（abstract data type） 属性-》成
阅读更多...
使用条件变量实现线程同步：C++实战指南

使用条件变量实现线程同步：C++实战指南

使用条件变量实现线程同步：C++实战指南 在多线程编程中，线程同步是确保程序正确性和稳定性的关键。条件变量（condition variable）是一种强大的同步原语，用于在线程之间进行协调，避免数据竞争和死锁。本文将详细介绍如何在C++中使用条件变量实现线程同步，并提供完整的代码示例和详细的解释。 什么是条件变量？ 条件变量是一种同步机制，允许线程在某个条件满足之前进入等待状态，并在条件满
阅读更多...
有关机械硬盘的基础知识

有关机械硬盘的基础知识

1，机械硬盘的品牌 　　目前市场中常见的笔记本电脑的机械硬盘品牌主要有希捷、西部数据、三星等。 　　2，机械硬盘的容量 　　硬盘容量，即硬盘所能存储的最大数据量。虽然笔记本电脑硬盘的容量会因单位密度的提升而增加，不过和台式电脑的大容量比起来，笔记本电脑硬盘的容量仍然落后许多。笔记本电脑的硬盘除了对磁盘有体积较小和数量较少的要求之外，对功耗、耐用程度、抗震性及成本等的考虑，也让笔记
阅读更多...
Java 入门指南：Java 并发编程 —— 并发容器 ConcurrentLinkedDeque

Java 入门指南：Java 并发编程 —— 并发容器 ConcurrentLinkedDeque

文章目录 ConcurrentLinkedDeque特点构造方法常用方法使用示例注意事项 ConcurrentLinkedDeque ConcurrentLinkedDeque 是 Java 并发工具包（java.util.concurrent 包）中的一个线程安全的双端队列（Deque）实现，实现了 Deque 接口。它使用了链表结构，并且针对高并发环境进行了优化，非常适合
阅读更多...
使用Nginx部署前端Vue项目的详细指南

使用Nginx部署前端Vue项目的详细指南

在本文中，我们将详细介绍如何使用Nginx部署一个前端Vue项目。此过程涵盖Vue项目的构建、Nginx的安装与配置、以及最后的项目启动。下面是步骤的详细说明。 步骤 1: 准备你的Vue项目 确保你已经创建并构建了一个Vue项目。如果你尚未创建Vue项目，可以使用以下命令创建一个： # 安装Vue CLInpm install -g @vue/cli# 创建一个新的Vue项目vue c
阅读更多...
【超级干货】2天速成PyTorch深度学习入门教程，缓解研究生焦虑

【超级干货】2天速成PyTorch深度学习入门教程，缓解研究生焦虑

3、cnn基础 卷积神经网络 输入层 —输入图片矩阵 输入层一般是 RGB 图像或单通道的灰度图像，图片像素值在[0,255]，可以用矩阵表示图片 卷积层 —特征提取 人通过特征进行图像识别，根据左图直的笔画判断X，右图曲的笔画判断圆 卷积操作 激活层 —加强特征 池化层 —压缩数据 全连接层 —进行分类 输出层 —输出分类概率 4、基于LeNet
阅读更多...
入门指南 | Datavines 安装部署篇

入门指南 | Datavines 安装部署篇

摘要：本文主要介绍基于源码部署 Datavines 和执行检查作业，内容主要分为以下几个部分： 平台介绍快速部署运行数据质量检查作业 Datavines 的目标是成为更好的数据可观测性领域的开源项目，为更多的用户去解决元数据管理和数据质量管理中遇到的问题。在此我们真诚欢迎更多的贡献者参与到社区建设中来，和我们一起成长，携手共建更好的社区。 https://github.com/dat
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2