本文主要是介绍MatLab建模学习笔记7——线性规划问题求解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
线性规划(Linear programming,简称LP)是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法。研究线性约束条件下线性目标函数的极值问题的数学理论和方法。
线性规划步骤一般如下:
(1)列出约束条件及目标函数
(2)画出约束条件所表示的可行域
(3)在可行域内求目标函数的最优解及最优值
线性规划中单纯形法的基本思路:先找出可行域的一个极点,据一定的规则来判断是否最优,否则转到与之相邻的另一极点,并使目标函数值更优;如此下去,直到找到最优解位置。线性规划在Matlab中的基本函数形式是:linprog(c,A,b),函数的返回的向量x,其中c代表线性方程的系数,是一个列向量;A代表约束方程参数的系数,b代表约束方程由常数构成的向量。
线性规划函数:[x,fval]=linprog(c,A,b,Aeq,Beq,LB,UB,X0,Options):其中Aeq和Beq代表等式约束Ax=b;LB,UB分别是变量X的上下界,X0是X的初始值,Options代表控制参数。
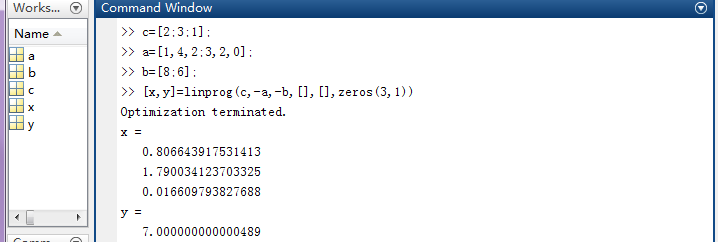
案例一:
min z=2*x1+3*x2+x3
Subject to:
x1+4*X2+2*X3>=8
3*X1+2*X2>=6
x1>=0
x2>=0
x3>=0
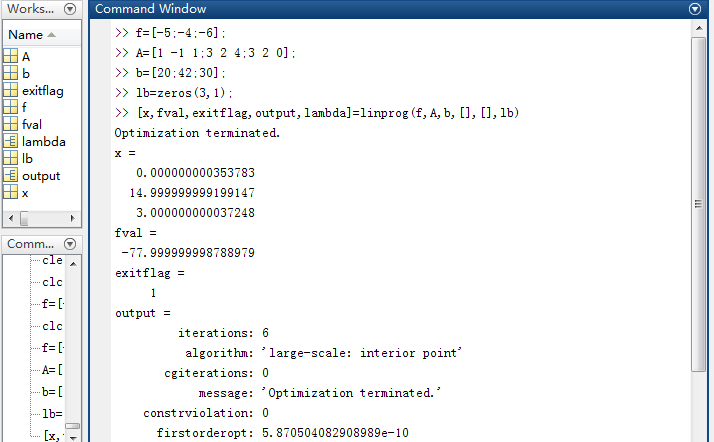
案例二:
min z=-5*x1-4*x2-6*x3
subject to:
x1-x2+x3<=20
3*x1+2*x2+4*x3<=42
3*x1+2*x2<=30
0<=x1
0<=x2
0<=x3
案例三:
max=2*x1+3*x2-5*x3
subject to:
x1+x2+x3=7
2*x1-5*x2+x3>=10
x1>=0
x2>=0
x3>=0
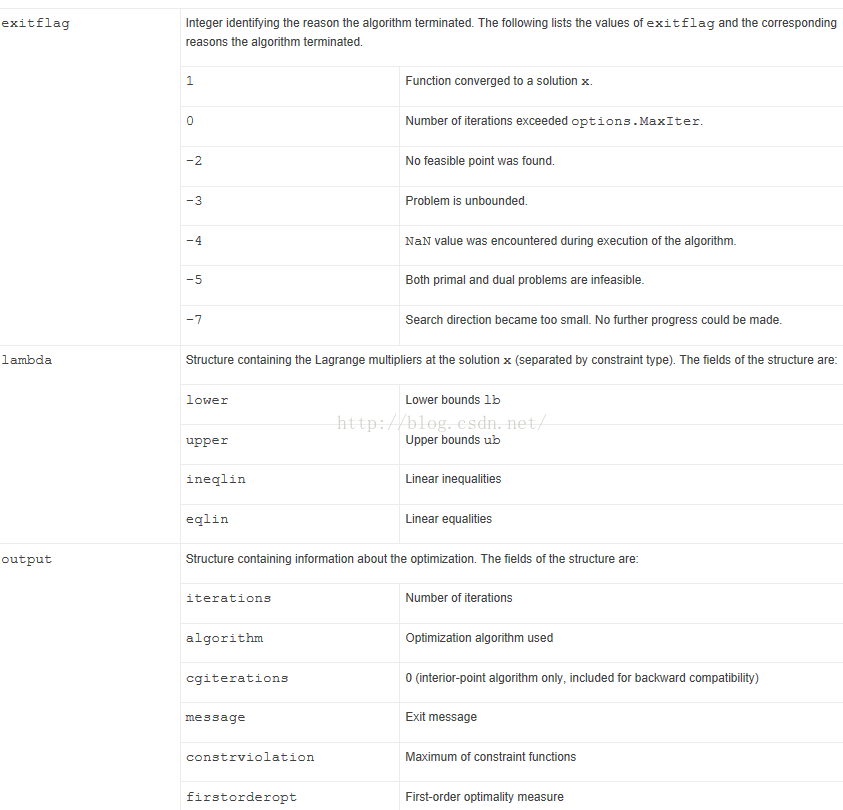
一些输出信息的意义如下:
这篇关于MatLab建模学习笔记7——线性规划问题求解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!