本文主要是介绍线性规划在多种问题形式下的应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
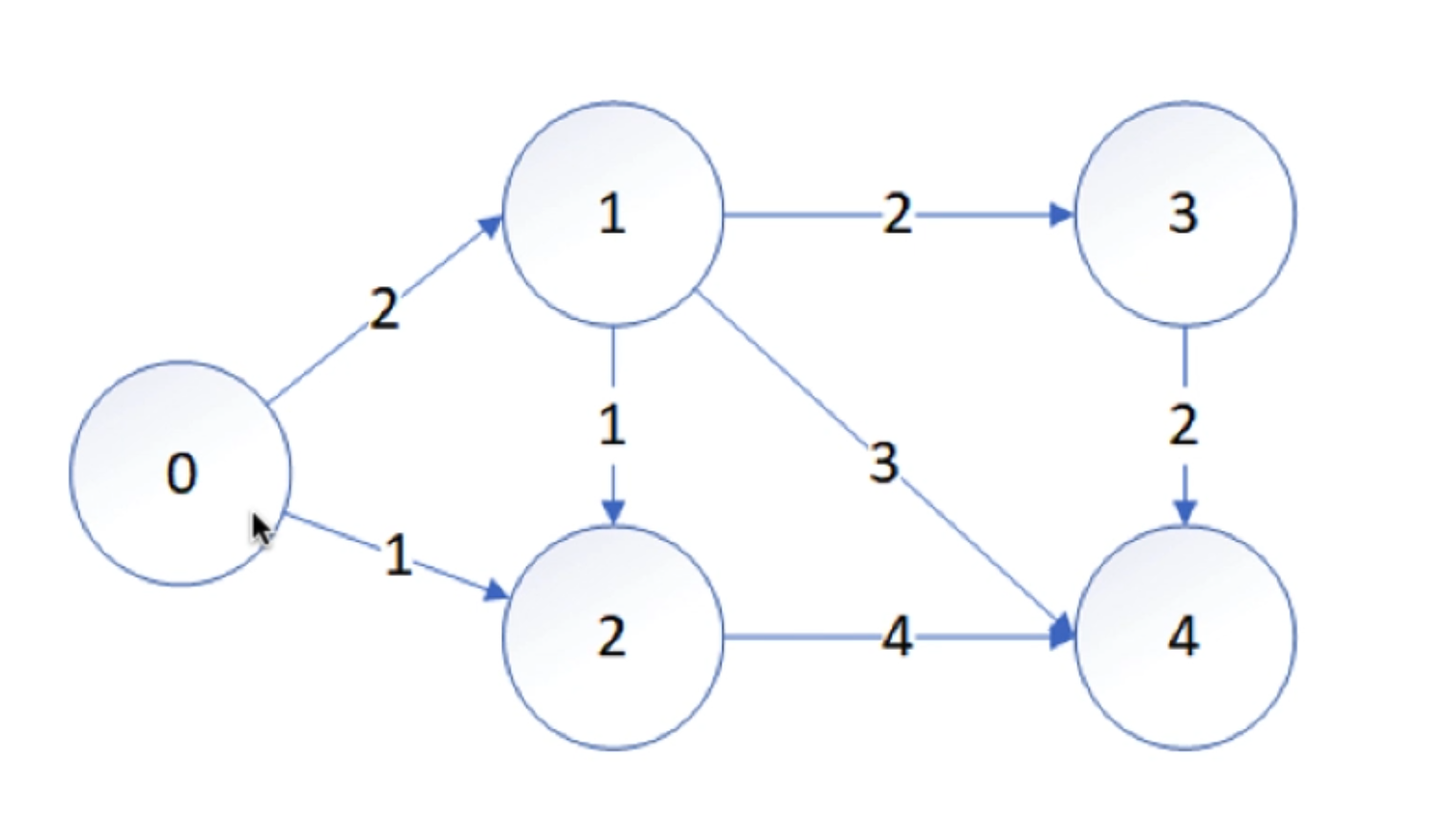
线性规划的用处非常的广泛,这主要是因为很多类型的问题是可以通过转化的方式转化为线性规划的问题。例如需要再图论中寻找起始点到给定的点的最短路径问题:
添加图片注释,不超过 140 字(可选)
假设要计算从节点0到节点4的最短路径,用变量d1到d4来表示节点0到节点1,2,3,4的最短路径,那么解决这个问题的本质上是解决如下的一个线性规划系统:
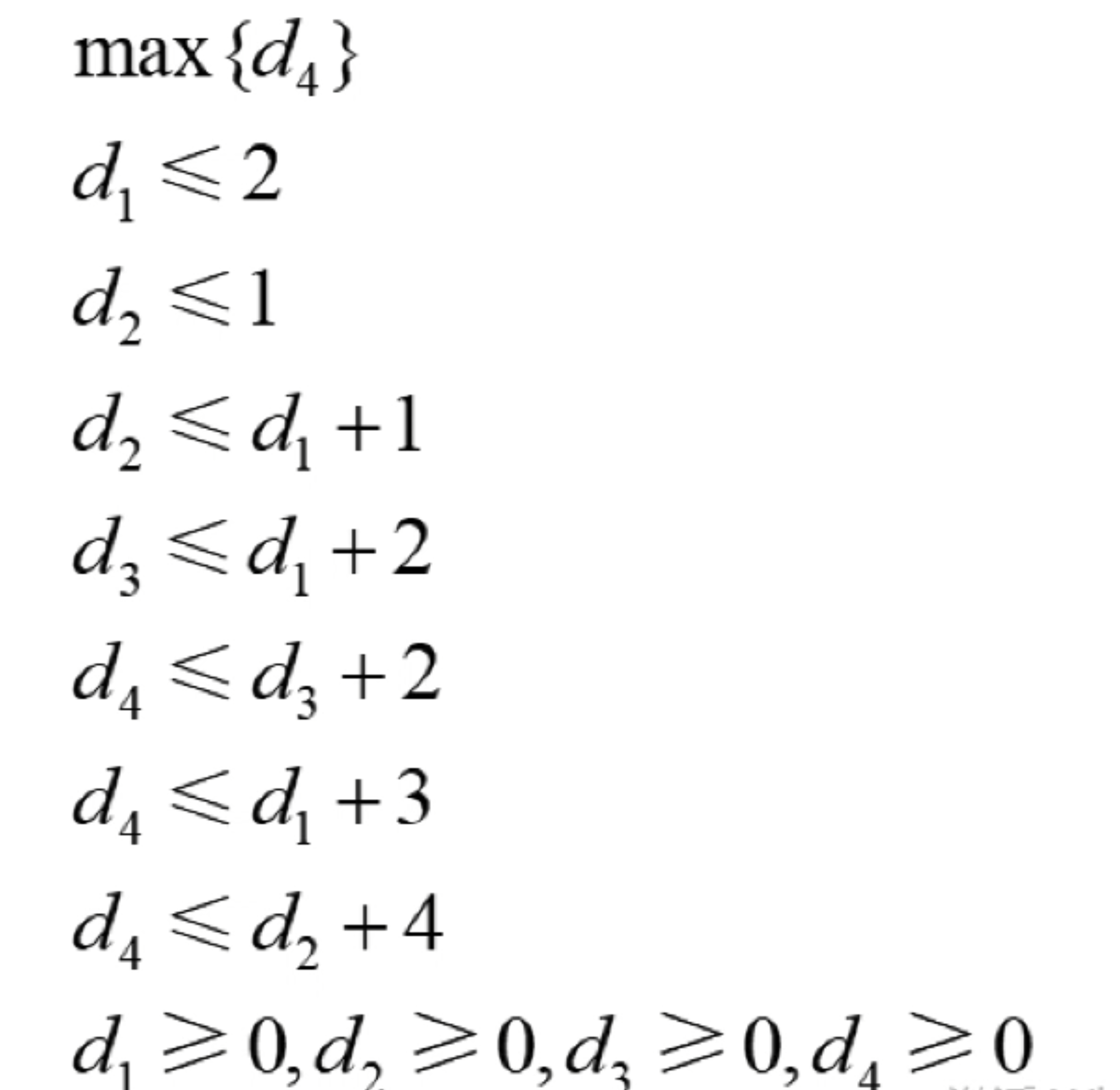
添加图片注释,不超过 140 字(可选)
而这里要注意的是问题所需要求的是最短路径,按照目标函数应该是查找最小值才对,但是这里是查找的最大值,因为如果查找最小值,那么问题的答案就是将所有变量设置为0,而这就与所需要的目标是不相符的。
由于最短路径肯定大于0,同时最短路径一定能满足上面线性系统的约束条件,且最大化可以让我们找到一个非零解,因此它才能对应正确的最短路径。
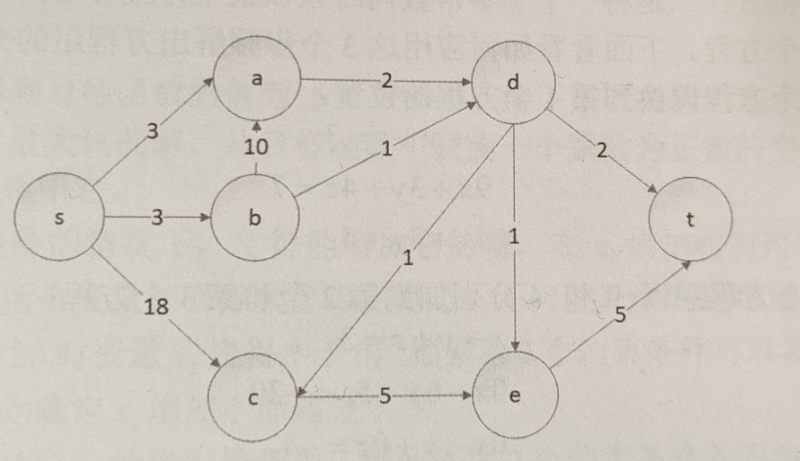
在图论中还存在一种称为极大流的问题,如果给定一个有向图G,其中有一个起点和一个终点,在两者之间存在很多中间点,同时点与点之间的连接存在一个容量上限,问题是从起点开始发出多少流量,这些流量分流到各个支路后,最终汇合到终点,试问起点能够发出的流量最大是多少
添加图片注释,不超过 140 字(可选)
上图中相互连接的节点其路径上的数字表示能够通过该路径的最大流量,例如边sa的值就是3,因此从节点s流向节点a的流量最大不能超过3,如果用c(u,v)来表示两个连接节点间的最大容量,如c(s,a)=3,那么就有c(u,v)>0,同时用f(u,v)表示从s点出发的最大流量经过每一条管道时的流量,那么就可以制定出对应的线性规划系统如下:
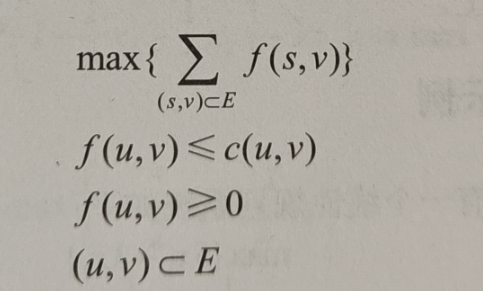
添加图片注释,不超过 140 字(可选)
这里的E表示所有边的集合,所以有很多类型的问题是可以通过转化成为线性规划问题的。
这篇关于线性规划在多种问题形式下的应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









