数学建模理论学习：线性规划模型

本文主要是介绍数学建模理论学习：线性规划模型，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

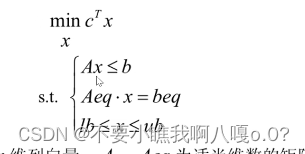
三要素：目标函数、约束条件（s.t.）、决策变量（x）

目标函数：z = ax1 + bx2 + cx3 + ...

其中c为一个序列，从左到右依次从x1到xn的系数

解决下面的线性规划问题：

% 目标函数系数：-x1 - 2x2
f = [-1; -2]; % 不等式约束 Ax <= b
% A向量表示决策变量的系数，B向量表示的是对应的条件，若不符合Ax <= b需进行初等变换
A = [1, 1; 2, 1; 1, 2];
b = [2; 3; 3];% 等式约束 Aeq x = beq（如果没有等式约束，则设置为空矩阵）
Aeq = [];
beq = [];% 变量下界和上界（如果没有界限约束，可以设置为空数组）
% lb表示决策变量的下界， ub表示决策变量的上界
lb = zeros(2, 1);
ub = [];% 调用 linprog 函数
[x, fval, exitflag, output] = linprog(f, A, b, Aeq, beq, lb, ub);% 显示结果
disp('最优解 x:')
disp(x)
disp('最优目标函数值 fval:')
disp(fval)
disp('退出标志 exitflag:')
disp(exitflag)
disp('输出信息 output:')
disp(output)

linprog函数：

[x, fval, exitflag, output] = linprog(f, A, b, Aeq, beq, lb, ub, options)

用linprog函数只能求解目标函数的最小值，如果我们需要求解最大值则需要加上符号变换一下即可：

% 建立目标函数
f = [-4, -3];% 建立约束条件
% Ax <= B
A = [2,1;1,1;0,1];
b = [40;8;7];
% A1x1 + A2x2 = B
Aeq = [];
Beq = [];
% x1, x2 的公共上界下界
lb = zeros(2,1);
ub = [];% 设置优化选项
options = optimoptions('linprog', 'Display', 'iter');% 求解线性规划结果
[x, fval, exitflag, output] = linprog(f, A, b, Aeq, Beq, lb, ub);
fval = -fval;% 输出结果
disp('最优解：')
disp(x)
disp('最优函数值：')
disp(fval)
disp(exitflag)
disp(output)

以下是对该目标函数的图像：

% 建立目标函数
f = [-4, -3];% 建立约束条件
A = [2, 1; 1, 1; 0, 1];
b = [40; 8; 7];% 变量下界
lb = zeros(2, 1);% 求解线性规划问题
[x, fval, exitflag, output] = linprog(f, A, b, [], [], lb, []);% 将最小化结果转换为最大化结果
fval = -fval;% 设置绘图范围
% 0 - 10 400个等间隔点的向量
x1 = linspace(0, 10, 400);
x2 = linspace(0, 10, 400);
% 0-10的正方形区间画等高线：
% 利用x1和x2两个向量声场两个400 * 400的矩阵X1, X2
[X1, X2] = meshgrid(x1, x2);% 计算目标函数值
Z = 4*X1 + 3*X2;% 绘制等高线
% 创建新的图形窗口
figure;
% 在指定范围内绘制20条等高线
contour(X1, X2, Z, 20); hold on;% 绘制约束条件
% 根据约束条件总结出约束范围：
fill([0, 0, 20, 20], [7, 0, 0, 7], 'b', 'FaceAlpha', 0.1); % x2 <= 7
fill([0, 8, 0], [8, 0, 0], 'g', 'FaceAlpha', 0.1); % x1 + x2 <= 8
fill([0, 20, 0], [0, 0, 40], 'r', 'FaceAlpha', 0.1); % 2x1 + x2 <= 40% 标记最优解
% MarkSize 标记点的大小 MarkFaceColor 标记点的颜色
plot(x(1), x(2), 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');% 标注和图例
xlabel('x1');
ylabel('x2');
title('线性规划问题的目标函数与约束条件');
legend('目标函数等高线', 'x2 <= 7', 'x1 + x2 <= 8', '2x1 + x2 <= 40', '最优解');
% 显示网格：
grid on;
% 取消绘图保持状态，使得下一次绘图会清除当前图形内容
hold off;

若目标函数不是线性函数：